C++ 是一种静态类型的、编译式的、通用的、大小写敏感的、不规则的编程语言,支持过程化编程、面向对象编程和泛型编程。
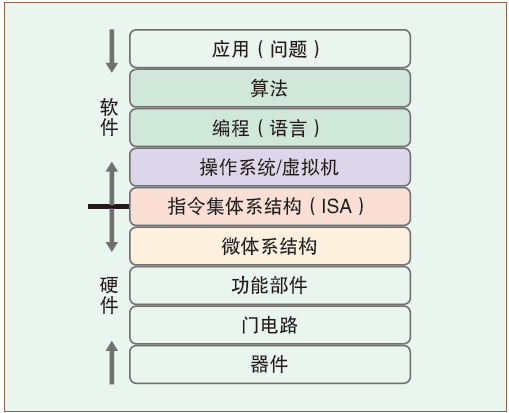
[学习笔记] - 计算机系统基础
[学习笔记] - Docker
Hexo 配置记录
[线性代数] - 四个子空间
[线性代数] - 投影
[数理统计] - 假设检验
在总体的分布函数完全未知或只知其形式,但不知道参数的情况,为了推断总体的某些未知特性,提出某些关于总体的假设。最常见的比如,有一组数据,这数据是某机器生产出来的产品的数据,假设机器的误差范围在0.1,那么通过假设检验可以判断机器是否在正常工作。
我们要根据样本对正态总体所提出假设做出是接受,还是拒绝的决策。