huhu's Blog

FLOWER ON THE PRECIPICE

[学习笔记] - 信息论

发表于 更新于 分类于
本文字数： 51k 阅读时长 ≈ 46 分钟

The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.

Shannon

信息论是用来找出信号处理与通信操作的基本限制，涉及

  • 数据压缩
  • 可靠的存储
  • 数据传输
  • …

要求

  1. 数理统计
  2. 概率论
  3. 最优化

通信系统模型

            graph LR
            subgraph 发信
信息-->信源编码;
信源编码-->加密;
加密-->信道编码;
信道编码-->数字调制;
end
数字调制--噪声源-->信道;
信道--噪声源-->数字调解;
subgraph 受信
数字调解-->信道译码;
信道译码-->解密;
解密-->信源译码;
信源译码-->受信者;
end

信息

信息：是事物运动状态或存在方式不确定性的描述，是对不确定性的消除

  • 不确定性：接收者在收到信息之前，对它的内容是不知道的
  • 信息能使认识主体对某一事物的未知性或不确定性减少
  • 信息使可以量度的

不确定性大小

f(p(x))f(p(x))

  • 必然事件：f(1)=0f(1) = 0
  • f(p(x))f(p(x))是单调减函数
  • 独立可加性：f(p(x)p(y))=f(p(x))+f(p(y))f(p(x)p(y)) = f(p(x)) + f(p(y))

概率空间

[XQ]=[x1x2⋯xnq(x1)q(x2)⋯q(xn)]\begin{bmatrix} X \\ Q \end{bmatrix}=\begin{bmatrix} x_1 & x_2 & \cdots & x_n \\ q(x_1) & q(x_2) & \cdots & q(x_n) \end{bmatrix}

  • 样本空间：信源所有可能发送的消息符号
  • 先验概率q(xi)q(x_i)：选择符号xix_i作为发送消息的概率

香农信息定义

优点：

  • 有明确的数学模型和定量计算公式
  • 与日常用于中的信息含意一致
  • 排除了对信息一词某些主观上的含意

局限性:

  • 没有考虑收信者的主观特性和主观意义
  • 定义的出发点假定事物状态可以用一个概率模型来描述

自信息

自信息量表示事件发生后，事件给予观察者的信息量（信息量：传输该信息所用的代价）。
是用来衡量单一事件发生时所包含的信息量多寡。

I(xi)=−log⁡q(xi)=log⁡1q(xi)I(x_i) = -\log q(x_i) = \log\frac{1}{q(x_i)}

自信息量的大小取决于事件发生的概率
比如说某一随机变量的概率为1/5 ， 那么它的自信息就是5比特。（自信息的单位是bite，比特）就是说这个随机变量带来5比特的信息。

  • 事件发生的可能性越大，它所包含的信息量就越小
  • 事件发生的概率越小，它能给与观察者的信息量就越大

性质：

  • 自信息量是非负的
  • 确定事件的信息量为零
  • 自信息量是概率的单调递减函数
  • I(x)I(x)基于随机变量X的特定取值x，不能作为整个随机变量X的信息测度

条件自信息

I(xi∣yi)=log1p(xi∣yj)I(x_i|y_i) = log\frac{1}{p(x_i|y_j)}

  • 后验概率p(xi∣yj)p(x_i|y_j)：接收端收到信息yjy_j后而发送端发的是xix_i的概率

非平均自信息

事件x,yx,y之间的互信息等于xx的自信息减去 yy条件下xx的自信息，非平均互信息的最值：

I(xk:yj)=logp(xk∣yj)q(xk)=I(xk)−I(xk∣yj)=log⁡−1q(xk)=−log⁡q(xk)\begin{aligned} I(x_k:y_j) &= log \frac{p(x_k|y_j)}{q(x_k)}=I(x_k) - I(x_k|y_j) \\ &= \log -\frac{1}{q(x_k)} \\ &= -\log q(x_k) \end{aligned}

当后验概率为1时，非平均互信息达到最大值（即无扰通信时所获取的信息最多）

离散变量的非平均自信息

对给定几何{X,q(kk)}\{X, q(k_k)\}，时间xk∈Xx_k \in X的自信息量定义为：

I(xk)=log⁡1q(xk)I(x_k) = \log \frac{1}{q(x_k)}

性质：集最大与最小于一身

I(xk:yj)≤I(xk)I(xk:yj)≤I(yj)\begin{aligned} I(x_k:y_j) &\leq I(x_k) \\ I(x_k:y_j) &\leq I(y_j) \end{aligned}

  • 自信息量
    • 是为了唯一（无歧义）确定事件xkx_k的出现所必须提供的信息量
    • 它也是其它任何事件所能提供的关于事件xk的最大信息量。自信息量具有非负性
    • 它的另外一种解释是先验不确定性的大小

非平均条件自信息

给定联合集{U1U2,p(u1u2)}\{U_1U_2 , p(u_1u_2)\}对事件u1∈U1u_1 \in U_1和u2∈U2u_2 \in U_2，事件u1u_1在事件u2u_2给定条件下的条件自信息量定义为

I(u1∣u2)=−log⁡p(u1∣u2)I(u_1|u_2) = -\log p(u_1|u_2)

含义：

  • 事件u2u_2给定条件下关于事件u1u_1的不确定性
  • 给定事件u2u_2时为唯一确定事件u1u_1的出现必须提供的信息量

非平均联合自信息

联合空间XY,p(xy){XY, p(xy)}中任一事件xy,x∈Xxy, x \in X和y∈Yy \in Y的联合自信息量定义为：

I(xy)≜−log⁡p(xy)I(xy) \triangleq -\log p(xy)

信息熵

香农信息熵函数满足的三个条件：

  • 连续性
  • 等概率时的单调增函数特性
  • 可加性

信息熵的性质

  • 对称性：对意义不关心，只关心概率

H(p1,p2,⋯ ,pn)=H(pk(1),pp(2),⋯ ,pk(n))H(p_1,p_2,\cdots,p_n) = H(p_k(1),p_p(2),\cdots,p_k(n))

  • 非负性

H(p)≥0H(p) \geq 0

  • 可加性

H(X,Y)=H(X)+H(Y∣X)H(X,Y) = H(X) + H(Y|X)

  • 条件减少性
    • 知道了统计相关性的变量，则可以减少不确定性
    • 统计平均意义上条件减少不确定性，但是针对具体的YY取值则不一定

H(X∣Y)≤H(X)H(X|Y) \leq H(X)

注意，这不是

H(X∣Y=y)≤H(X)H(X|Y=y) \leq H(X)

  • 离散随机变量XX在等概率分布时，熵取得最大值

H(X1,X2,⋯ ,Xn)≤H(1N,1N,⋯ ,1N)=log⁡N=log⁡∣X∣H(X_1,X_2,\cdots,X_n) \leq H(\frac{1}{N},\frac{1}{N}, \cdots, \frac{1}{N}) = \log N = \log |X|

信息熵本质上是对我们司空见惯的不确定现象的数学化度量

离散随机变量X的信息熵

对于一个离散型随机变量X∼p(x)X \sim p(x)

H(X)=−∑x∈Xp(x)log⁡p(x)=E[log⁡1p(X)]H(X) = \color{red}-\sum_{x\in \mathcal{X}}p(x)\log p(x)\color{black} = E\big[\log \frac{1}{p(X)}\big]

  • 熵实际上是随机变量XX的函数log⁡1p(X)\log \frac{1}{p(X)}的期望
  • HH的综量是随机变量的分布，而非取值
  • 0log⁡0(x→0,xlog⁡x→0)0\log 0(x \rightarrow 0, x\log x\rightarrow 0)概率为0的时间不影响信息熵
  • 熵与一组信息的可压缩性紧密联系在一起
  • 熵为信息的不可再降低的复杂度，即不可能再被压缩
  • 约定0log⁡0=00\log 0 = 0，因为零概率的项不改变熵的值

如果使用底为bb的对数，则相应的熵记为Hb(X)H_b(X)，当对数底为ee时，熵的单位用奈特

Hb(X)=(log⁡ba)Ha(X)H_b(X) = (\log_b a)H_a(X)

唯一性：

g(MN)=f(1MN,⋯ ,1MN)=f(1M,⋯ ,1M)+∑i=1n1Mf(1N,⋯ ,1N)=g(M)+g(N)g(Sm)=g(S⋅Sm−1)=g(S)+g(Sm−1)=mg(S)\begin{aligned} g(MN) &= f(\frac{1}{MN},\cdots,\frac{1}{MN}) = f(\frac{1}{M}, \cdots, \frac{1}{M}) + \sum^n_{i=1}\frac{1}{M}f(\frac{1}{N}, \cdots, \frac{1}{N}) \\ &= g(M) + g(N) \\ g(S^m) &= g(S\cdot S^{m-1}) = g(S) + g(S^{m-1}) \\ &= mg(S) \end{aligned}

取s,m,t,n∈Ns, m, t, n \in N，使得sm≤tn≤sm+1s^m \leq t^n \leq s^m+1，则

g(sm)≤g(tn)≤g(sm+1)mg(s)≤ng(t)≤(m+1)g(sm)mn≤g(t)g(s)<m+1n\begin{aligned} g(s^m) &\leq g(t^n) &\leq g(s^m+1) \\ mg(s) &\leq ng(t) &\leq (m+1)g(s^m) \\ \frac{m}{n} &\leq \frac{g(t)}{g(s)} &< \frac{m+1}{n} \end{aligned}

于是∣mn−g(t)g(s)∣<1n|\frac{m}{n} - \frac{g(t)}{g(s)}| < \frac{1}{n}

由

mlog⁡S≤nlog⁡t<(m+1)log⁡Sm\log S \leq n\log t < (m+1)\log S

得到

∣mn−log⁡tlog⁡s∣<1n|\frac{m}{n} - \frac{\log t}{\log s}| < \frac{1}{n}

使用∣a±b∣≤∣a∣+∣b∣|a \pm b| \leq |a| + |b|，得到

∣g(t)g(s)−log⁡tlog⁡s∣≤2n|\frac{g(t)}{g(s)} - \frac{\log t}{\log s}| \leq \frac{2}{n}

让nn趋近+∞+\infty得到

g(t)g(s)→log⁡tlog⁡s\frac{g(t)}{g(s)} \rightarrow \frac{\log t}{\log s}

于是g(t)=Clog⁡tg(t) = C\log t

假设分布律X∼Px(x)X \sim P_x(x)，令P(n)P(n)为

P(n)=mn∑i=1nmi=mnMg(M)=f(1M,⋯ ,1M)=f(P1,P2,⋯ ,PN)+∑i=1NmnMg(mn)\begin{aligned} P(n) &= \frac{m_n}{\sum^n_{i=1}m_i} = \frac{m_n}{M} \\ g(M) &= f(\frac{1}{M}, \cdots, \frac{1}{M}) \\ &= f(P_1, P_2, \cdots, P_N) + \sum^N_{i=1}\frac{m_n}{M}g(m_n) \end{aligned}

现在看看f(P1,P2,⋯ ,PN)f(P_1, P_2, \cdots, P_N)是什么形式

f(P1,P2,⋯ ,PN)=g(M)−∑i=1MPig(mi)=Clog⁡M−∑i=1MPiClog⁡mi=Clog⁡M(∑Pi)−∑i=1MPiClog⁡mi=−C∑i=1MPi(log⁡mi−log⁡M)=−C∑Pilog⁡Pi\begin{aligned} f(P_1, P_2, \cdots, P_N) &= g(M) - \sum^M_{i=1}P_ig(m_i) \\ &= C\log M - \sum^M_{i=1}P_iC\log m_i \\ &= C\log M(\sum P_i) - \sum^M_{i=1}P_iC\log m_i \\ &= -C\sum^M_{i=1}P_i(\log m_i - \log M) \\ &= -C \sum P_i\log P_i \end{aligned}

联合熵

一对离散随机变量(X,Y)(X, Y)的联合熵定义为：

H(X,Y)=−∑x∈X∑y∈Yp(x,y)log⁡p(x,y)=E[log⁡1p(x,y)]H(X, Y) = -\sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}} p(x, y)\log p(x, y) = E\big[\log \frac{1}{p(x, y)}\big]

意义：观察一个多个随机变量的随机系统获得的信息量

条件熵

若(X,Y)∼p(x,y)(X, Y) \sim p(x, y)，则条件熵H(Y∣X)H(Y|X)定义为：

H(Y∣X)=∑x∈Xp(x)H(Y∣X=x)=−∑x∈Xp(x)∑y∈Yp(y∣x)log⁡p(y∣x)=−∑x∈X∑y∈Yp(x,y)log⁡p(y∣x)\begin{aligned} H(Y|X) &= \sum_{x \in \mathcal{X}}p(x)H(Y|X = x) \\ &= -\sum_{x \in \mathcal{X}}p(x)\sum_{y \in \mathcal{Y}}p(y|x)\log p(y|x) \\ &= -\sum_{x \in \mathcal{X}}\sum_{y \in\mathcal{Y}}p(x, y)\log p(y|x) \end{aligned}

条件熵与联合熵的关系

H(X,Y)=H(X)+H(Y∣X)=H(Y)+H(X∣Y)\begin{aligned} H(X,Y) &= H(X) + H(Y|X) \\ &= H(Y) + H(X|Y) \end{aligned}

由统计的公式，两边取对数再取期望

p(x,y)=p(x)p(y∣x)p(x, y) = p(x)p(y|x)

可以证明出

若X,YX, Y统计独立，则

H(X,Y)=H(X)+H(Y)H(X,Y) = H(X) + H(Y)

在得知某一确定信息的基础上获取另外一个信息时所获得的信息量。

定理：设随机变量X1X2⋯XnX_1X_2\cdots X_n满足分布p(x1,x2,⋯ ,xn)p(x_1,x_2,\cdots,x_n)，则

H(X1,X2,⋯ ,Xn)=∑i=1nH(Xi∣Xi−1⋯X1)H(X_1,X_2,\cdots,X_n) = \sum^n_{i=1}H(X_i|X_{i-1}\cdots X_1)

互信息

  • 事物时普遍联系的，随机变量之间也存在相互关系

假设有以下关系

            graph LR
            随机变量X --某种操作和联系--> 随机变量Y;
  • 单独观察XX，得到的信息量是H(X)H(X)
  • 已知YY之后，XX的信息量变为H(X∣Y)H(X|Y)
  • 了解了YY之后，XX的信息量减少了H(X)−H(X∣Y)H(X) - H(X|Y)
  • 这个减少量是得知YY取值之后提供的关于XX的信息

互信息I(X:Y)I(X: Y)则表示为知道事实YY后，原来信息量减少了多少。

离散随机变量XX与YY之间的互信息为

I(X:Y)={H(X)−H(X∣Y)∑x∈X∑y∈Yp(x,y)logp(x,y)p(x)p(y)H(X)+H(Y)−H(X,Y)I(X: Y)= \begin{cases} H(X) - H(X|Y) \\ \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y)log\frac{p(x,y)}{p(x)p(y)} \\ H(X) + H(Y) - H(X,Y) \end{cases}

  • 若X,YX, Y独立，则I(X,Y)=0I(X, Y) = 0
  • 若X,YX, Y一一映射，则I(X,Y)=H(X)I(X, Y) = H(X)

假定XX是信道的输入，Y是信道的输出

            graph LR
            输入信道X-p --信道转移概率矩阵Q--> 信道输出Y;
  • 用pp和Q=[q(y∣x)]Q = [q(y|x)]表示互信息
    • I(X;Y)=I(p;Q)=∑x∈X∑y∈Yp(x)q(y∣x)logq(y∣x)p(x)q(y∣x)I(X;Y) = I(\mathbf{p};\mathbf{Q}) = \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x)q(y|x)log\frac{q(y|x)}{p(x)q(y|x)}
    • p\mathbf{p}：信道输入的条件分布
    • Q\mathbf{Q}：信道的噪声模型
  • I(X;Y)I(X;Y)表示了一个信道输入与输出之间的依赖关系→\rightarrow信道的传输能力

多变量的互信息

设有随机变量X,YX,Y与ZZ之间的互信息为

I(X;Y;Z)={H(X)−H(X∣Y,Z)=H(Y,Z)−H(Y,Z∣X)∑x∈X∑y∈Y∑z∈Zp(x,y,z)logp(x∣y,z)p(x)∑x∈X∑y∈Y∑z∈Zp(x,y,z)logp(x,y,z)p(x)p(y,z)I(X;Y;Z)= \begin{cases} H(X) - H(X|Y,Z) = H(Y,Z) - H(Y,Z|X) \\ \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} \sum_{z \in \mathcal{Z}} p(x,y,z)log\frac{p(x|y,z)}{p(x)} \\ \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} \sum_{z \in \mathcal{Z}} p(x,y,z)log\frac{p(x,y,z)}{p(x)p(y,z)} \end{cases} 

            graph LR
            随机变量X --某种操作或联系--> 输出;

多变量的条件互信息

设有随机变量X,YX,Y与ZZ

I(X;Y∣Z)={H(X∣Z)−H(X∣Y,Z)H(Y∣Z)−H(Y∣X,Z)∑x∈X∑y∈Y∑z∈Zp(x,y,z)logp(x,y∣z)p(x∣z)p(y∣z)H(X∣Z)−H(X,Y∣Z)+H(Y∣Z)H(X,Z)−H(Z)−H(X,Y,Z)+H(Z)+H(Y,Z)−H(Z)H(X,Z)+H(Y,Z)−H(X,Y,Z)−H(Z)I(X;Y|Z) = \begin{cases} H(X|Z) - H(X|Y,Z) \\ H(Y|Z) - H(Y|X,Z) \\ \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} \sum_{z \in \mathcal{Z}} p(x,y,z)log\frac{p(x,y|z)}{p(x|z)p(y|z)} \\ H(X|Z) - H(X,Y|Z) + H(Y|Z) \\ H(X,Z) - H(Z) - H(X,Y,Z) + H(Z) + H(Y,Z) - H(Z) \\ H(X,Z) + H(Y,Z) - H(X, Y, Z) - H(Z) \end{cases}

  • 条件互信息非负：I(X;Y)≥0I(X;Y) \geq 0
  • 对称性：I(X;Y)=I(Y;X)I(X;Y) = I(Y;X)
  • 极值性：I(X;Y)≤min(H(X),H(Y))I(X;Y) \leq min(H(X), H(Y))
    • 2个随机变量的互信息不可能提供比随机变量自身还大的信息量
  • 可加性：I(X1,X2,⋯ ,Xn∣Y)=∑i=1n(Xi;Y∣X1,⋯ ,Xi−1)I(X_1,X_2,\cdots,X_n|Y) = \sum^n_{i=1}(X_i;Y|X_1,\cdots,X_{i-1})
    • 互信息可以分布获得

信息论的证明

  • Achievability：可达性
    • 用某种编码或压缩的方法，证明某一个特定的指标是可以实现的
  • Converse：逆
    • 你不可能比某一个边界更好
    • 若与Achievability相等，则证明达到最好

鉴别信息（相对熵）

两个概率密度函数p(x)p(x)和q(x)q(x)之间的鉴别信息（交叉熵，相对熵）定义为

D(p∥q)=∑x∈Xp(x)logp(x)q(x)D(\mathbf{p}\parallel\mathbf{q}) = \sum_{x \in \mathcal{X}}p(x)log\frac{p(x)}{q(x)}

  • 两个概率密度函数的距离的度量
    • 当真实分布为pp而假定分布为qq时的无效性
  • p=qp=q时，鉴别信息为00
  • 鉴别信息非负
  • 不是严格距离上的距离
    • 不具有对称性
    • 不具有三角不等式的关系

熵，互信息，鉴别信息的关系

  • 离散变量的熵与鉴别信息的关系满足（u\mathbf{u}为均匀分布）
    • log⁡∣X∣\log|X|是最大熵，在分布为u\mathbf{u}的时候取得
    • D(p∥u)D(\mathbf{p}\parallel\mathbf{u})是均匀分布与实际分布之间的差异的度量

H(X)=log⁡∣X∣−D(p∥u)H(X) = \log |X| - D(\mathbf{p}\parallel\mathbf{u})

  • 香农熵是由均匀分布走向实际分布过，所减少的那部分信息量从均匀分布中所减去剩余的那一部分
  • 当分布律未知时，最合理的推断的分布为均匀分布
    • log⁡∣X∣\log |X|：均匀分布下的信息量

离散变量的互信息与鉴别信息的关系满足

I(X;Y)=D(p(x,y)∥p(x)p(y))I(X;Y) = D(p(x,y)\parallel p(x)p(y))

意义：当随机变量X,YX,Y分布p(x,y)p(x,y)时，我们假定二者独立，上述定义给出这种假定距离实际情况差异大小

名字 公式 意义
熵 H(X)=−∑x∈Xp(x)log⁡p(x)H(X) = -\sum_{x\in \mathcal{X}}p(x)\log p(x) 不确定现象的数学化度量
联合熵 H(X,Y)=−∑x∈X∑y∈Yp(x,y)log⁡p(x,y)H(X, Y) = -\sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}} p(x, y)\log p(x, y) 观察一个多个随机变量的随机系统获得的信息量
条件熵 H(Y∣X)=∑x∈Xp(x)H(Y∣X=x)H(Y\vert X) = \sum_{x \in \mathcal{X}}p(x)H(Y \vert X = x) 在得知某一确定信息的基础上获取另外一个信息时所获得的信息量
自信息 I(xi)=−log⁡q(xi)I(x_i) = -\log q(x_i) 事件给予观察者的信息量
互信息 I(X:Y)=H(X)−H(X∣Y)I(X: Y)=H(X) - H(X\vert Y) 知道事实YY后，原来信息量减少了多少
鉴别信息 D(p∥q)=∑x∈Xp(x)logp(x)q(x)D(\mathbf{p}\parallel\mathbf{q}) = \sum_{x \in \mathcal{X}}p(x)log\frac{p(x)}{q(x)} 某一个随机变量2种分布的距离

注意：H(Y∣X)≠H(X∣Y)H(Y|X) \neq H(X|Y)，但是H(X)−H(X∣Y)=H(Y)−H(Y∣X)H(X) - H(X|Y) = H(Y) - H(Y|X)

Jenson不等式

如果ff是下凸函数，且XX是离散随机变量，则

Ef(X)≥f(EX)Ef(X) \geq f(EX)

并且，若ff是严格下凸函数，上式的等号说明XX为常数，即XX与EXEX以概率1相等

  • 统计平均可以看作是一个线性组合的操作
  • 函数的统计平均大于等于统计平均的函数值

对数求和不等式

对于非负实数a1,a2,⋯ ,ana_1,a_2,\cdots,a_n和b1,b2,⋯ ,bnb_1,b_2,\cdots,b_n有

∑i=1nailog⁡aibi≥(∑i=1nai)log⁡∑i=1nai∑i=1nbi\sum^n_{i=1}a_i\log\frac{a_i}{b_i} \geq (\sum^n_{i=1}a_i) \log \frac{\sum^n_{i=1}a_i}{\sum^n_{i=1}b_i}

等号当且仅当aibi\frac{a_i}{b_i}为常数的时候成立

证明：

设函数f(t)=tlog⁡t,(t>0)f(t) = t\log t, (t>0)是凸函数

∑aif(ti)≥f(∑aiti)\begin{aligned} \sum a_i f(t_i) \geq f(\sum a_it_i) \end{aligned}

令ai=biB,ti=aibi,b=∑bia_i = \frac{b_i}{B}, t_i = \frac{a_i}{b_i}, b= \sum b_i，则

∑biBaibilog⁡aibi≥∑biBaibilog⁡∑biB∑(ailog⁡aibi)≥∑ailog⁡∑ai∑bi\begin{aligned} \sum \frac{b_i}{B}\frac{a_i}{b_i}\log \frac{a_i}{b_i} &\geq \sum \frac{b_i}{B} \frac{a_i}{b_i} \log \sum \frac{b_i}{B} \\ \sum(a_i \log \frac{a_i}{b_i}) &\geq \sum a_i \log \frac{\sum a_i}{\sum b_i} \end{aligned}

鉴别信息的凸性

D(p∥u)D(\mathbf{p}\parallel\mathbf{u})是(p,q)(p,q)的下凸函数，即若存在分布对(p1,q1)(p_1,q_1)和(p2,q2)(p_2,q_2)，则

D(λp1+(1−λ)p2∥λq1+(1−λ)q2)≤λD(p1∥q1)+(1−λ)D(p2∥q2)D(\lambda p_1 + (1 - \lambda)p_2 \parallel \lambda q_1 + (1 - \lambda)q_2) \leq \lambda D(p_1 \parallel q_1) + (1 - \lambda)D(p_2\parallel q_2)

对于所有0≤λ≤10 \leq \lambda \leq 1成立
上述式子的即：这两个分布对的线性组合之间的鉴别信息是小于两个鉴别信息的线性组合

证明：

设λ∈[0,1],λ‾=1−λ\lambda \in [0, 1], \overline{\lambda} = 1 - \lambda

λp1(x)+λ‾p2(x)log⁡λp1(x)+λ‾p2(x)λq1(x)+λ‾q2(x)≤λp1(x)p1(x)q1(x)+λ‾p2(x)log⁡p2(x)q2(x)D(λp1+λp2∥λq1+λ‾q2)≤λD(p1∥q1)+λ‾D(p2∥q2)\begin{aligned} \lambda p_1(x) + \overline{\lambda}p_2(x)\log\frac{\lambda p_1(x) + \overline{\lambda}p_2(x)}{\lambda q_1(x) + \overline{\lambda} q_2(x)} &\leq \lambda p_1(x)\frac{p_1(x)}{q_1(x)} +\overline{\lambda}p_2(x)\log \frac{p_2(x)}{q_2(x)} \\ D(\lambda p_1 + \lambda p_2 \parallel \lambda q_1 + \overline{\lambda} q_2) &\leq \lambda D(p_1 \parallel q_1) + \overline{\lambda}D(p_2\parallel q_2) \end{aligned}

熵的上凸性

熵函数是随机分布pp的上凸函数

H(px)=log⁡∣X∣−D(px∥u)=linear−convex=concave\begin{aligned} H(p_x) &= \log |X| - D(p_x\parallel \mathbf{u}) \\ &= linear - convex \\ &= concave \end{aligned}

信源→X0∼p0(x)信源编码器→X′∼p0(x)\text{信源} \xrightarrow{\quad X_0 \sim p_0(x)\quad} \text{信源编码器} \xrightarrow{\quad X' \sim p_0(x)\quad}

具有相同熵的两种气体混合后，熵必定增大

互信息的上凸性

            graph LR
            输入信道X-p --信道转移概率矩阵Q--> 信道输出Y;

固定QQ，互信息是pp的上凸函数

证明：

固定Q=[q(y∣x)]Q = [q(y|x)]

I(X;Y)=H(Y)−H(Y∣X)=H(Y)−∑x∈Xp(x)H(Y∣X=x)\begin{aligned} I(X;Y) &= H(Y) - H(Y|X) \\ &= H(Y) - \sum_{x \in \mathcal{X}} p(x)H(Y|X=x) \end{aligned}

我们注意到H(Y)H(Y)是基于Px(x)P_x(x)的上凸函数

H(Y∣X)=∑xp(x)∑yq(y∣x)log⁡1q(y∣x)H(Y|X) = \sum_x p(x) \sum_y q(y|x) \log \frac{1}{q(y|x)}

可以知道H(X∣Y)H(X|Y)是基于Px(x)P_x(x)的线性函数，即I(X;Y)I(X;Y)针对Px(x)P_x(x)是上凸的

Fano不等式

定义错误概率：Pe=Pr{X^≠X}P_e = Pr\lbrace \hat{X} \neq X \rbrace

→随机变量X处理→随机变量Y处理→估计值X^\xrightarrow{\quad \text{随机变量}X \quad} \text{处理} \xrightarrow{\quad \text{随机变量}Y \quad} \text{处理} \xrightarrow{\quad \text{估计值}\hat{X} \quad}

对于任意估计X^\hat{X}，满足X→Y→X^X \rightarrow Y \rightarrow \hat{X}，且Pe=Pr{X^≠X}P_e = Pr\lbrace \hat{X} \neq X \rbrace，则

H(Pe)=Pelog⁡∣X∣≥H(X∣X^)≥H(X∣Y)H(P_e) = P_e \log |X| \geq H(X|\hat{X}) \geq H(X|Y)

证明

定义分布EE为

E={0,X=X^1,X≠X^⟹H(E)=H(Pe)E = \begin{cases} 0, &X=\hat{X} \\ 1, &X\neq \hat{X} \end{cases} \Longrightarrow H(E) = H(P_e)

观察一下等式

H(E,X∣X^)+H(X∣X^)+H(E∣X,X^)=H(X∣X^)H(E, X|\hat{X}) + H(X|\hat{X}) + H(E|X,\hat{X}) = H(X|\hat{X})

当X,X^X,\hat{X}取值都已知的情况下，H(E∣X,X^)=0H(E|X,\hat{X}) = 0，再观察

H(E,X∣X^)=H(E∣X^)+H(X∣E,X^)≤H(Pe)+PeH(X∣X^≠X,X^)+(1−Pe)H(X∣X^=X,X^)≤H(Pe)+Pelog⁡∣X∣\begin{aligned} H(E, X|\hat{X}) &= H(E|\hat{X}) + H(X|E,\hat{X}) \\ &\leq H(P_e) + P_e H(X|\hat{X} \neq X, \hat{X}) + (1- P_e) H(X|\hat{X} = X, \hat{X}) \\ &\leq H(P_e) + P_e\log |X| \end{aligned}

即可得出

H(X∣X^)≤H(Pe)+Pelog⁡∣X∣H(X|\hat{X}) \leq H(P_e) + P_e\log |X|

数据处理不等式

当我们有了一系列数据处理的操作，且彼此之间独立，随着处理流程的推进，处理出来的结论，它与原始的素材之间的互信息是不会增加的，只会越来越小，称为数据处理定理

p(x,y,z)=p(x)p(y∣x)p(z∣y)⇒X→Y→Zp(x, y, z) = p(x)p(y|x)p(z|y) \Rightarrow X \rightarrow Y \rightarrow Z

以上称为马尔科夫链

X→Y→ZX \rightarrow Y \rightarrow Z蕴含Z→Y→XZ \rightarrow Y \rightarrow X

I(X;Y)≥I(X;Z)I(X;YZ)=I(X;Y)+I(X;Z∣Y)=I(X:X^)+I(X;Y∣Z)I(X;Y)≥I(X;Z)H(X∣Z)≥H(X∣Y)\begin{aligned} \\ I(X;Y) &\geq I(X;Z) \\ I(X;YZ) &= I(X;Y) + I(X;Z|Y) \\ &= I(X:\hat{X}) + I(X;Y|Z) \\ \\ I(X;Y) &\geq I(X;Z) \\ H(X|Z) &\geq H(X|Y) \end{aligned}

连续随机变量的微分熵

定义连续随机变量

  • 微分熵

h(X)=−∫−∞+∞p(x)log⁡p(x)dxh(X) = -\int^{+\infty}_{-\infty} p(x)\log p(x)dx

  • 联合熵

h(X,Y)=−∬p(x,y)log⁡p(x,y)dxdyh(X, Y) = -\iint p(x ,y)\log p(x, y)dxdy

  • 条件熵

h(X∣Y)=−∬p(x,y)log⁡p(x∣y)dxdy=−∫p(y)∫p(x∣y)log⁡p(x∣y)dxdy\begin{aligned} h(X|Y) &= -\iint p(x, y) \log p(x|y)dxdy \\ &= -\int p(y) \int p(x|y) \log p(x|y) dxdy \end{aligned}

  • 不等式关系

h(X,Y)=h(X)+h(Y∣X)=h(Y)+h(X∣Y)h(X∣Y)≤h(X),h(Y∣X)≤h(X)h(X,Y)≤h(X)+h(Y)\begin{aligned} h(X, Y) &= h(X) + h(Y|X) = h(Y) + h(X|Y) \\ h(X|Y) &\leq h(X),\quad h(Y|X) \leq h(X) \\ h(X,Y) &\leq h(X) + h(Y) \end{aligned}

h(x)h(x)不一定为正

正态分布的微分熵

  • 正态分布

X:p(x)=12πσe−(x−u)22σ2−∞<x<∞X: p(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-u)^2}{2\sigma^2}} \quad -\infty < x < \infty

  • 正态分布微分熵的计算

h(X)=−∫−∞+∞p(x)log⁡p(x)dx=−∫−∞+∞p(x)log⁡(12πσe−(x−u)22σ2)dx=−∫−∞+∞p(x)log⁡12πσdx+log⁡e∫−∞+∞p(x)(x−u)22σ2dx=log⁡2πσ2+log⁡e2σ2∫−∞+∞p(x)(x−m)2dx=log⁡2πσ2+12log⁡e=12log⁡2πeσ2\begin{aligned} h(X) &= -\int^{+\infty}_{-\infty} p(x)\log p(x)dx \\ &= -\int^{+\infty}_{-\infty} p(x)\log (\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-u)^2}{2\sigma^2}}) dx \\ &= -\int^{+\infty}_{-\infty} p(x)\log \frac{1}{\sqrt{2\pi}\sigma} dx + \log e \int^{+\infty}_{-\infty} p(x) \frac{(x-u)^2}{2\sigma^2} dx \\ &= \log \sqrt{2\pi \sigma^2} + \frac{\log e}{2\sigma^2}\int^{+\infty}_{-\infty} p(x)(x-m)^2dx \\ &= \log \sqrt{2\pi \sigma^2} + \frac{1}{2}\log e \\ &= \frac{1}{2}\log 2\pi e \sigma^2 \end{aligned}

h(X)=12log⁡2πeσ2\color{red}h(X) = \frac{1}{2}\log 2\pi e \sigma^2

  • σ2\sigma^2：该随机信号的功率
  • 如果一个连续随机变量服从正态分布，它带来的信息量与均值μ\mu无关，只与功率σ2\sigma^2有关
  • 若给定连续随机变量XX的均值μ\mu与方差σ2\sigma^2，则当其服从正态分布时，微分熵最大

连续随机变量的互信息

采用类似于微分熵的推广方法求随机变量变量的互信息为

I(X;Y)=lim⁡Δx→0Δy→0∑i=−∞+∞∑j=−∞+∞p(xi,yj)ΔxiΔyilog⁡p(xi,yiΔxiΔyi)p(xi′)Δxip(yj′)Δyi=∬p(x,y)log⁡p(x,y)p(x)p(y)dxdy\begin{aligned} I(X;Y) &= \lim_{\Delta x\rightarrow 0\Delta y\rightarrow 0} \sum^{+\infty}_{i = -\infty}\sum^{+\infty}_{j = -\infty} p(x_i, y_j) \Delta x_i \Delta y_i \log \frac{p(x_i,y_i\Delta x_i \Delta y_i)}{p(x'_i)\Delta x_i p(y'_j)\Delta y_i} \\ &= \iint p(x,y)\log \frac{p(x,y)}{p(x)p(y)} dxdy \end{aligned}

信源

渐进等同分割性质

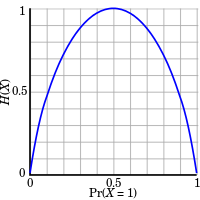
最大离散熵原理：等概分布时，离散熵最大化
问题：如何将非等概率输出的信源变成等概

一个随机变量，他是均匀分布的，我们对他进行一个定长的切割，如下图

  • 每一段的长度由1→+∞1 \rightarrow +\infty
  • 这样差不多所有的事件都是等概出现的
  • 可以简单地由弱大数定理推出
  • 对于数据压缩有贡献
    • 等同分割⟶\longrightarrow等概率⟶\longrightarrow最大离散熵⟶\longrightarrow定长编码定理
    • 暗示了一种定长编码的方法

如果X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n是独立同分布的离散随机变量，分布服从p(x)p(x)，则

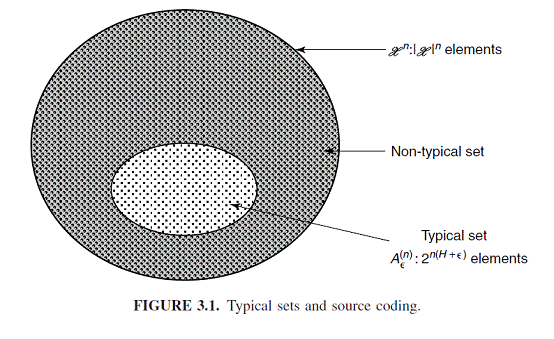
1nlog⁡p(X1,X2,⋯ ,Xn)→PH(X)\frac{1}{n} \log p(X_1, X_2, \cdots, X_n) \xrightarrow{\quad P \quad} H(X)

典型序列

相对于分布p(x)p(x)和序列(x1,x2,⋯ ,xn)∈Xn(x_1, x_2, \cdots, x_n) \in X_n，典型序列集合Aε(n)A^{(n)}_\varepsilon定义为满足下列不等式约束的所有序列xx的集合

2−n(H(X)+ε)≤p(x)=p(x1,x2,⋯ ,xn)≤2−n(H(X)−ε)2^{-n(H(X) + \varepsilon)} \leq p(\mathbf{x}) = p(x_1, x_2, \cdots, x_n) \leq 2^{-n(H(X) - \varepsilon)}

  • 若x∈Aε(n)\mathbf{x} \in A^{(n)}_\varepsilon，则H(X)−ε≤−1nlog⁡p(x)≤H(X)−εH(X) - \varepsilon \leq -\frac{1}{n} \log p(\mathbf{x}) \leq H(X) - \varepsilon
  • 若nn足够大，Pr{Aε(n)}>1−εPr\lbrace A^{(n)}_\varepsilon\rbrace > 1 - \varepsilon，即几乎总是看到典型序列
  • ∣Aε(n)∣≤2n(H(X)+ε)|A^{(n)}_\varepsilon| \leq 2^{n(H(X) + \varepsilon)}
  • ∣Aε(n)∣≥(1−ε)2n(H(X)+ε)|A^{(n)}_\varepsilon| \geq (1 - \varepsilon)2^{n(H(X) + \varepsilon)}
  • 典型序列的集合只是所有集合的一个子集，但是几乎一定会出现，且数量大概为

2nH(X)2^{nH(X)}

  • 随着nn的增大，所有典型序列出现的概率，几乎是一样的，几率大概是

2−nH(X)2^{-nH(X)}

证明：

  • 性质三

1=∑xn∈Xp(xn)≥∑xn∈Aε(n)p(xn)≥∑xn∈Aε(n)2−n(H(X)+ε)=2−n(H(X)+ε)∣Aε(n)∣∣Aε(n)∣≤2n(H(X)+ε)\begin{aligned} 1 &= \sum_{x^n \in \mathcal{X}} p(x^n) \\ &\geq \sum_{x^n \in A^{(n)}_\varepsilon} p(x^n) \\ &\geq \sum_{x^n \in A^{(n)}_\varepsilon} 2^{-n(H(X) + \varepsilon)} \\ &= 2^{-n(H(X) + \varepsilon)}|A^{(n)}_\varepsilon| \\ \\ |A^{(n)}_\varepsilon| &\leq 2^{n(H(X) + \varepsilon)} \end{aligned}

  • 性质四

1−ε≤P0{Aε(n)}≤∑xn∈Aε(n)2−n(H(X)−ε)=2−n(H(X)−ε)∣Aε(n)∣∣Aε(n)∣≥(1−ε)2n(H(X)−ε)\begin{aligned} 1 - \varepsilon &\leq P_0\lbrace A^{(n)}_\varepsilon \rbrace \\ &\leq \sum_{x^n \in A^{(n)}_\varepsilon} 2^{-n(H(X) - \varepsilon)} \\ &= 2^{-n(H(X) - \varepsilon)}|A^{(n)}_\varepsilon| \\ \\ |A^{(n)}_\varepsilon| &\geq (1 - \varepsilon)2^{n(H(X) - \varepsilon)} \end{aligned}

定长编码定理

设XnX^n是由独立同分布离散随机变量x∼P(x)x \sim P(x)构成的序列，对于任意正数ε\varepsilon，总有足够大的nn，可以找到一个一一映射，将XnX^n
映射为二进制序列，且满足

E[1nl(Xn)]≥H(X)+εE\big[\frac{1}{n}l(X^n)\big] \geq H(X) + \varepsilon

使用nH(X)nH(X)比特足以描述nn个独立同分布的随机变量

证明：

E(l(Xn))=∑xn∈Xn=∑xn∈Aεnp(xn)l(xn)+∑xn∈Aεn‾p(xn)l(xn)E(l(X^n)) = \sum_{x^n \in \mathcal{X}^n} = \sum_{x^n \in \mathcal{A}^n_\varepsilon} p(x^n)l(x^n) + \sum_{x^n \in \overline{\mathcal{A}^n_\varepsilon}} p(x^n)l(x^n)

也就是，将一段序列分为nn段，每一段的长度，等于典型序列长度的期望++非典型序列长度的期望，由典型序列的性质三，我们可以得到下面的式子

E(l(Xn))≤∑xn∈Aεnp(xn)[n(H(X)+ε)+1+1]+∑xn∈Aεn‾p(xn)[nlog⁡∣X∣+1+1]E(l(X^n)) \leq \sum_{x^n \in \mathcal{A}^n_\varepsilon} p(x^n) [n(H(X) + \varepsilon) + 1 + 1] + \sum_{x^n \in \overline{\mathcal{A}^n_\varepsilon}} p(x^n) [n\log |X| + 1 + 1]

其中

  • 第一个+1+1是为了保证n(H(X)+ε)n(H(X) + \varepsilon)是整数
  • 第二个+1+1是为了标识现在编码是一个(非)典型序列，而不是其他的，用来作区分
  • 对于非典型（后边的式子），索性全部编码

进行化简可以得到

=Pr{Aε(n)}[n(H+ε)+2]+Pr{A‾ε(n)}[nlog⁡∣X∣+2]= P_r\lbrace A^{(n)}_\varepsilon \rbrace [n(H+\varepsilon) + 2] + P_r \lbrace \overline{A}^{(n)}_\varepsilon \rbrace [n\log |X| + 2]

其中

{Pr{Aε(n)}<1Pr{A‾ε(n)}<ε\begin{cases} P_r\lbrace A^{(n)}_\varepsilon \rbrace < 1 \\ P_r\lbrace \overline{A}^{(n)}_\varepsilon \rbrace < \varepsilon \end{cases}

即可得到

≤n(H+ε)+2+nεlog⁡∣X∣+2ε=n(H+ε′),ε′=ε+εlog⁡∣X∣+2εn\begin{aligned} &\leq n(H+\varepsilon) + 2 + n\varepsilon\log |X| + 2\varepsilon \\ &= n(H + \varepsilon'), \qquad \varepsilon' = \varepsilon + \varepsilon\log |X| + \frac{2\varepsilon}{n} \end{aligned}

其中对于ε′\varepsilon'

n→∞,ε′→0n \rightarrow \infty, \quad \varepsilon' \rightarrow 0

其含义为，当nn趋向∞\infty，每一段的期望大小逼近nHnH

例题：设信源输出符号分布为

(Xp(x))=(a1a2a3a4a5a6a7a80.400.180.100.100.070.060.050.04)\begin{pmatrix} X \\ p(x) \end{pmatrix}=\begin{pmatrix} a_1 & a_2 & a_3 & a_4 & a_5 & a_6 & a_7 & a_8 \\ 0.40 & 0.18 & 0.10 & 0.10 & 0.07 & 0.06 & 0.05 & 0.04 \end{pmatrix}

希望编码错误概率小于10−810^{-8}，且编码效率大于90%90\%，求最小可行分组长度

解：

编码效率=H(X)用长度为n的典型序列编码后每个信源字母的平均符号数>H(X)H(X)+ε>0.9\begin{aligned} \text{编码效率} &= \frac{H(X)}{\text{用长度为}n\text{的典型序列编码后每个信源字母的平均符号数}} \\ &> \frac{H(X)}{H(X) + \varepsilon} > 0.9 \end{aligned}

解得ε<0.28\varepsilon < 0.28，而编码错误概率为P{A‾ε(n)}P\lbrace\overline{A}^{(n)}_\varepsilon\rbrace，即非典型序列出现的概率，有

P{A‾ε(n)}≤D(I(X))Nε2≤10−8P\lbrace\overline{A}^{(n)}_\varepsilon\rbrace \leq \frac{D(I(X))}{N\varepsilon^2} \leq 10^{-8}

计算可得

N>D(I(X))10−8ε2>1.3110−8⋅(0.28)2>108N > \frac{D(I(X))}{10^{-8}\varepsilon^2} > \frac{1.31}{10^{-8}\cdot(0.28)^2} > 10^8

非奇异码

若一个码CC可以将不同的xx映射为不同的D∗D^*中的序列，即

x≠x′⇒C(x)≠C(x′)x \neq x' \Rightarrow C(x) \neq C(x')

则称该码是非奇异的，类似映射的单射

  • 非奇异码可以将符号唯一的恢复，但是当信源输出符号序列的时候，会失败
    • 例如：C(x1)=0,C(x2)=1,C(x3)=01C(x_1) = 0, C(x_2) = 1, C(x_3) = 01就会出错
  • 解决的方法是再输出码字之间加入间隔符，这是低效的做法
  • 解决方法是寻找自断句的码方案

唯一课译码

称码C∗C^*是码CC的扩展，当C∗C^*是有限长XX的序列到有限长D−D-进制序列的映射，且满足

C(x1x2⋯xn)=C(x1)C(x2)⋯C(xn)C(x_1x_2\cdots x_n) = C(x_1)C(x_2)\cdots C(x_n)

  • 例如：C(x1)=00,C(x2)=11,C(x1x2)=0011C(x_1) = 00, C(x_2) = 11, C(x_1x_2) = 0011

称码CC是唯一可译码，当其扩展是非奇异的

  • 也就是说：没有码字是码字的组合
  • 例如C(x1)=0,C(x2)=01,C(x3)=11C(x_1) = 0, C(x_2) = 01, C(x_3) = 11，则序列00110010唯一可译为x1x1x3x1x2x1x_1x_1x_3x_1x_2x_1
  • 但是，此时译码需要"回退"，即要缓存来判别

即时码

称一个码是即时码或者前缀码，当没有码字是其他码字的前缀

  • 即时码可以立刻译出，而无需借助后续的码字信息
  • 例如：C(1)=0,C(2)=10,C(3)=110,C(4)=111C(1) = 0,C(2) = 10,C(3) = 110,C(4) = 111
    • 则系列01011111010可以立刻断句为0,10,111,110,10
  • 前缀码是一种具有很好性质的码

前缀码约束条件 - Kraft不等式

  • 欲用即时前缀码对信源进行编码
  • 显然不能使用所有的最短的码字，否则前缀码的条件将无法满足

任意D−D-进制码前缀码其码长l1,l2,⋯ ,lml_1, l_2, \cdots, l_m，满足

∑iD−li≤1\sum_i D^{-l_i} \leq 1

反之，若码长约束满足上述不等式，则必然可以构造出一个具有此码长的前缀码

  • Kraft不等式给出了即时码（前缀码）的充要条件
  • Kraft不等式是纯粹编码构造的考虑，与码是否最优无关

任意前缀码码长的约束

对随机变量XX进行D−D-进制前缀码编码，得到的码长LL满足

L≥HD(X)L \geq H_D(X)

等号当且仅当D−li=piD^{-l_i} = p_i时成立

  • 物理意义：平均码长不会比熵率更小
  • 与由APE导出的定长编码定理结论一致
  • HD(X)H_D(X)：以DD为底的熵

证明：

L−H(X)=∑pili−∑pilog⁡1pi=∑pilog⁡DDei+∑pilog⁡Dpi\begin{aligned} L - H(X) &= \sum p_i l_i - \sum p_i \log \frac{1}{p_i} \\ &= \sum p_i\log_DD^{e_{i}} + \sum p_i \log_D p_i \end{aligned}

令rir_i为经验分布D−eiΔ\frac{D^{-e_i}}{\Delta}，Δ=∑D−ei\Delta = \sum D^{-e_i}，于是

L−H(X)=D(p∥r)+log⁡1Δ≥0\begin{aligned} L - H(X) &= D(p\parallel r) + \log \frac{1}{\Delta} \geq 0 \end{aligned}

  • 其中鉴别信息D(p∥r)>≥0D(p\parallel r) > \geq 0（鉴别信息的性质）
  • Δ≤1⇒log⁡1Δ≥0\Delta \leq 1 \Rightarrow \log \frac{1}{\Delta} \geq 0

即可得到

L≥H(X)L \geq H(X)

即证明了，用D−D-进制前缀码对于随机变量XX进行编码，得到的所有的码字的平均长度都大于HD(X)H_D(X)

香农第一定理（最优前缀码定理）

对随机变量XX进行D−D-进制前缀码编码，得到的最优码长L∗L^*满足下列不等式

HD(X)≤L∗<HD(X)+1H_D(X) \leq L^* < H_D(X) + 1

证明：

取⌈log⁡1pi⌉\left \lceil \log \frac{1}{p_i} \right \rceil为码字长度，则

∑D−⌈log⁡1pi⌉≤∑Dlog⁡1p1=∑pi=1log⁡D1pi≤li≤log⁡D1pi+1HD(X)≤∑pili≤HD(X)+1HD(X)≤L∗≤∑pili=Lshammo≤HD(X)+1\begin{aligned} \sum D^{-\left \lceil \log \frac{1}{p_i} \right \rceil} &\leq \sum D^{\log \frac{1}{p_1}} = \sum p_i = 1 \\ \log_D\frac{1}{p_i} &\leq l_i \leq \log_D\frac{1}{p_i} + 1 \\ H_D(X) &\leq \sum p_il_i \leq H_D(X) + 1 \\ H_D(X) &\leq L^* \leq \sum p_il_i = L_{shammo} \leq H_D(X) + 1 \end{aligned}

分组前缀码

对于信源XX进行分组前缀编码，得到的每消息符号数Ln∗Ln^*满足不等式

H(X1,X2,⋯ ,Xn)n≤Ln∗<H(X1,X2,⋯ ,Xn)n+1n\frac{H(X_1,X_2,\cdots,X_n)}{n} \leq Ln^* < \frac{H(X_1,X_2,\cdots,X_n)}{n} + \frac{1}{n}

进一步，若信源稳恒，有

Ln∗→H(X)Ln^* \rightarrow H(\mathcal{X})

编码效率与互信息

  • 最优前缀码的编码与信源的分布密切相关
  • 如果对信源分布估计出现差错，对码长也会有影响（Penalty）

对于服从p(x)p(x)信源XX进行前缀编码，若码字长度取l(x)=⌈log⁡1pi⌉l(x) = \left \lceil \log \frac{1}{p_i} \right \rceil，则平均码长满足

H(p)+D(p∥q)≤Epl(X)<H(p)+D(p∥q)+1H(p) + D(p\parallel q) \leq E_pl(X) < H(p) + D(p\parallel q) + 1

这里的意义也就是，我们认为我们知道XX的分布，但是其实我们不知道，这里码长的增加量也就是我们估计错的惩罚

Shannon编码

li=⌈log⁡1pi⌉l_i = \left \lceil \log \frac{1}{p_i} \right \rceil

  • Shannon编码虽然可以满足编码定理给出的1 bite/符号的开销约束，但是一般情况下不是最优的编码

Huffman编码

  • Huffman编码具有最优性
  • 在给定信源符号的概率分布和码字母表的前提下，没有其他编码可以获得比Huffman编码更短的平均码长

考虑对具有以下分布的无记忆稳恒信源进行二进制Huffman编码

(123450.250.250.20.150.15)\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 0.25 & 0.25 & 0.2 & 0.15 & 0.15 \end{pmatrix}

  • 当D≥3D \geq 3时，需要填充概率为零的字母进入信源字母表，以保证编码顺利进行
  • 每次迭代缩减，减少的信源字母个数为D−1D - 1个，因此填充后信源字母总个数应该为1+k(D−1)1 + k(D - 1)个

最优码由很多，将一个最优码码字的位倒叙，交换具有相同长度的两个码字，都是另外一个最优码

对任意一个分布，必然存在满足如下性质的一个最优即时码

  • 其长度序列与按概率分布列排序的次序相反
  • 最长的两个码字具有相同长度
  • 最长的两个码字仅在最后一位上有所差别，且对应于两个最小可能发送的字符

信道容量

  • 通信是什么
    • 物理实体A的作用引发了物理实体B的状态变化
    • 若A与B的状态变化存在一致性，称A与B通信成功
  • 从信息角度看通信本质
    • 比特流的端到端无差错复制

→信息信道编码器→x∗信道q(y|x)→y∗信道解码器→w′消息的估计\xrightarrow{\quad \text{信息} \quad} \text{信道编码器} \xrightarrow{\quad x^*\quad} \text{信道q(y|x)} \xrightarrow{\quad y^*\quad} \text{信道解码器} \xrightarrow{\quad w'\text{消息的估计}\quad}

信道的分类

  • 按照输入输出的形式和时间取值来划分
取值 时间 信道分类
离散 离散 离散信道、数字信道
连续 离散 连续信道
连续 连续 模拟信道
离散 连续

按照信道随机过程的特点分类

  • 信道可以表示为n−n-阶转移概率矩阵

Qt1t2⋯tn={q(yt1t2⋯tn∣xt1t2⋯tn)}Q_{t_1t_2\cdots t_n} = \lbrace q(\mathbf{y}_{t_1t_2\cdots t_n}|\mathbf{x}_{t_1t_2\cdots t_n}) \rbrace

  • 无记忆信道
    • 由输出到输出转移的行为是彼此不相关
    • 信道噪声的特性是彼此不相关

q(y1y2⋯yn∣x1x2⋯xn)=∏i=1nq(yi∣xi)q(y_1y_2\cdots y_n|x_1x_2\cdots x_n) = \prod^n_{i=1}q(y_i|x_i)

  • 一般认为信道是平稳的
    • 在时间上的任何一个断面去看，统计特性都是不变的

q(yi∣xi)=q(y∣x)q(y_i|x_i) = q(y|x)

离散无记忆信道（DMC）

X→Q={q(y∣x)}YX \xrightarrow{\quad Q = \lbrace q(y|x)\rbrace \quad}Y

  • 互信息

I(Xn;Yn)=H(Yn)−H(Yn∣Xn)≤∑i=1nI(xi;yi)H(Yn)=H(Y1)+H(Y2∣Y1)+H(Y3∣Y1Y2)+⋯≤∑i=1nH(Yi)H(Yn∣Xn)=−EX,Ylog⁡q(yn∣xn)=−EX,Ylog⁡∏i=1nq(yi∣xi)=−−EX,Y∑i=1nlog⁡q(yi∣xi)=−∑i=1n−EX,Ylog⁡q(yi∣xi)=∑i=1nH(Yi∣Xi)\begin{aligned} I(X^n;Y^n) &= H(Y^n) - H(Y^n|X^n) \leq \sum^n_{i=1}I(x_i;y_i) \\ \\ H(Y^n) &= H(Y_1) + H(Y_2|Y_1) + H(Y_3|Y_1Y_2) + \cdots \\ &\leq \sum^n_{i=1}H(Y_i) \\ \\ H(Y^n|X^n) &= -E_{X,Y} \log q(y^n|x^n) = -E_{X,Y} \log \prod^n_{i=1} q(y_i|x_i) \\ &= --E_{X,Y} \sum^n_{i=1} \log q(y_i|x_i) \\ &= -\sum^n_{i=1} -E_{X,Y} \log q(y_i|x_i) \\ &= \sum^n_{i=1} H(Y_i|X_i) \end{aligned}

信道输入和输出的互信息 ≤\leq 每一个时刻互信息求和
有多字母表述走向单字母表述，为了求最大

  • 求等号
  • 使I(xi;yi)I(x_i;y_i)最大

离散无记忆信道的输入和输出

设信道输入X=(X1,X2,⋯ ,Xm)\mathbf{X}=(X_1,X_2,\cdots,X_m)，输出为Y=(Y1,Y2,⋯ ,Yn)\mathbf{Y} = (Y_1,Y_2,\cdots,Y_n)，对于离散无记忆信道，有

I(X;Y)≤∑i=1nI(Xi;Yi)I(\mathbf{X}; \mathbf{Y}) \leq \sum^n_{i=1}I(X_i;Y_i)

信道容量的定义

对于离散无记忆信道，信道容量为：

C=max⁡p(x)I(X;Y)=max⁡p(x)I(p,Q)\color{red}C = \max_{p(x)} I(X;Y) = \max_{p(x)}I(p,\mathbf{Q})

  • 关于信道容量
    • C的量纲：比特
    • 最大值：跑遍所有输入分布的条件下获得的

离散无记忆信道容量

  • 无噪声二元信道

由于信息无差错，所以每次传输都传递了1比特的无差错信息，直观的，信道容量为1bit

C=max⁡I(X;Y)=H(X)−H(X∣Y)=max⁡H(X)=1bitp(x)=(0.5,0.5)\begin{aligned} C &= \max I(X; Y) = H(X) - H(X|Y) \\ &= \max H(X) = 1bit \\ \\ &p(x) = (0.5,0.5) \end{aligned}

  • 输出不重叠的噪声信道
  • 信道存在噪声，因而输出不确定
  • 不确定性不影响正确估计输入
  • 因此，信道实际是无差错的

C=max⁡I(X;Y)=H(X)−H(X∣Y)=max⁡H(X)=1bitp(x)=(0.5,0.5)\begin{aligned} C &= \max I(X; Y) = H(X) - H(X|Y) \\ &= \max H(X) = 1bit \\ \\ &p(x) = (0.5,0.5) \end{aligned}

  • 二进制对称信道

C=max⁡p(x)I(X;Y)\begin{aligned} C = \max_{p(x)} I(X;Y) \end{aligned}

关注

I(X;Y)=H(Y)−H(Y∣X)=H(Y)−H(p)≤1−H(p)CBSC=1−H(p)\begin{aligned} I(X;Y) &= H(Y) - H(Y|X) \\ &= H(Y) - H(p) \\ &\leq 1 - H(p) \\ \\ C_{BSC} &= 1 - H(p) \end{aligned}

  • 删除信道

I(X;Y)=H(Y)−H(Y∣X)=H(Y)−H(p)=H((π(1−p),p,(1−π,1−p)))−H(p)=(1−p)H(π)+H(p)−H(p)=(1−p)H(π)≤1−pCBSC=1−p\begin{aligned} I(X;Y) &= H(Y) - H(Y|X) \\ &= H(Y) - H(p) \\ &= H((\pi(1-p), p, (1-\pi, 1-p))) - H(p) \\ &=(1-p)H(\pi) + H(p) - H(p) \\ &= (1-p)H(\pi) \\ &\leq 1-p \\ \\ C_{BSC} &= 1 - p \end{aligned}

其中pp是删除信道出错的概率

对称信道

若信道的转移概率矩阵的

  • 行互为置换，列互为置换，称该信道对称
  • 行互为置换，各列之和相等，称该信道弱对称

[121316161213131612][131612131216]\begin{bmatrix} \frac{1}{2} & \frac{1}{3} & \frac{1}{6} \\ \frac{1}{6} & \frac{1}{2} & \frac{1}{3} \\ \frac{1}{3} & \frac{1}{6} & \frac{1}{2} \\ \end{bmatrix} \qquad \begin{bmatrix} \frac{1}{3} & \frac{1}{6} & \frac{1}{2} \\ \frac{1}{3} & \frac{1}{2} & \frac{1}{6} \\ \end{bmatrix}

  • H(Y∣X)H(Y|X)是不已XX的分布为转移的，始终是一个常数

弱对称信道

弱对称信道QQ的容量为

C=log⁡∣Y∣−H(Q的行向量对应的分布)C = \log |Y| - H(Q\text{的行向量对应的分布})

容量在输入为等概率分布的时候取得

一般无记忆离散信道

由I(p,Q)I(p, Q)是pp的上凸函数，求信道容量问题可以表述成一个约束极值问题

maxI(p,Q)s.t.∑Xp(x)=1p(x)≥0\begin{aligned} max & \quad I(p, Q) \\ s.t. & \quad \sum_X p(x) = 1 \\ & \quad p(x) \geq 0 \end{aligned}

  • 求解方法
    • 拉格朗日乘数法
    • 梯度搜索法
    • 迭代解法

对于信道矩阵为QQ的离散无记忆信道，其输入分布p∗p^*能使互信息I(p,Q)I(p ,Q)取得最大值的充要条件是

I(X=xk;Y)=Cxk:p∗(xk)>0I(X=xk;Y)≤Cxk:p∗(xk)=0\begin{aligned} I(X = x_k;Y) = C & x_k:p^*(x_k) > 0 \\ I(X = x_k;Y) \leq C & x_k:p^*(x_k) = 0 \end{aligned}

其中

I(X=xk;Y)=∑j=1Jq(yj∣xk)log⁡q(yj∣xk)p(yj)I(X = x_k;Y) = \sum^J_{j=1} q(y_j|x_k) \log \frac{q(y_j|x_k)}{p(y_j)}

表示的是信源字母xkx_k传送的平均互信息，CC为信道容量

可以对任何一个离散无记忆信道进行信道容量的单字母表达下的计算

Kuhn-Tucker条件

设f(x)f(x)为定义在N维无穷凸集S={x=(x1,x2,⋯ ,xn):xi≥0,i=1,2,⋯ ,NS = \lbrace x = (x_1, x_2, \cdots, x_n) : x_i \geq 0, i= 1,2,\cdots, N上的可微上凸函数，设x∗=(x1∗,x2∗,⋯ ,xn∗)∈Sx^* = (x^*_1, x^*_2, \cdots, x^*_n) \in S，则f(x)f(x)在x=x∗x = x^*达到SS上的极大值的充要条件是

∂f(x)∂xn∣x=x∗=0,if xn∗>0∂f(x)∂xn∣x=x∗≤0,if xn∗=0\begin{aligned} \frac{\partial f(x)}{\partial x_n} \big |_{x = x^*} = 0, if\ x^*_n > 0 \\ \frac{\partial f(x)}{\partial x_n} \big |_{x = x^*} \leq 0, if\ x^*_n = 0 \end{aligned}

  • x∗=(x1∗,x2∗,⋯ ,xn∗),xn∗>0x^* = (x^*_1, x^*_2, \cdots, x^*_n), x^*_n > 0时，x∗x^*为SS的内点，∃xn∗=0\exists x^*_n = 0时，x∗x^*为SS的边界点。
  • 此条件是充要条件

信道的组合

级联的独立信道

            graph LR
            Start --X--> 信道Q1;
信道Q1 --Y--> 信道Q2;
信道Q2 --Z--> End;
  • 数据处理定理：I(Y;Z)≥I(X;Z)I(Y;Z) \geq I(X;Z)
  • 一般的，随着串联信道数目的增多，其容量趋近于0
  • 将联级信道的QiQ_i乘起来，得到整个级联信道的QQ，即可求解级联信道的容量
  • Vision：从统计的角度上看，数据处理不会带来增益，反而会丢失信息

输入并联信道

  • 特点：输入相同的XX，输出不同的Y1,Y2,⋯Y_1,Y_2,\cdots构成随即矢量YY
  • 输入并联信道的容量大于任何一个单独的信道，小于max H(X)max\ H(X)
  • NN个二元堆成信道输入并联之后的信道容量，NN越大，CNC_N越大，越接近H(X)H(X)
  • Vision通信中的分集，就是典型的输入并联信道
            graph LR
            X--X1-->信道1;
X--X2-->信道2;
X--Xn-->信道n;
信道1--Y1-->Y;
信道2--Y2-->Y;
信道n--Yn-->Y;

并联信道

            graph LR
            X--X1-->信道1;
X--X2-->信道2;
X--Xn-->信道n;
信道1--Y1-->Y;
信道2--Y2-->Y;
信道n--Yn-->Y;
  • 多输入，多输出，XX和YY由彼此独立的NN个信道传输
  • 并用信道的容量：C=∑n=1NCnC = \sum^N_{n=1}C_n
  • Vision通信中的复用，就是典型的并用信道
  • 例子:ADSL拨号上网，蜂窝网络

和信道

            graph LR
            X-->信道1;
X-->信道2;
X-->信道n;
信道1-->Y;
信道2-->Y;
信道n-->Y;
  • 随机应用NN个信道中的一个，构成一输入/输出信道
  • 和信道的容量是：C=log⁡∑n=1N2CnC = \log \sum^N_{n=1} 2^{C_n}
  • 信道的使用概率：pn(C)=2(Cn−C)p_n(C) = 2^{(C_n - C)}
  • Vision：一种新型的通信技术

(1−ε1ε1∣00ε11−ε1∣00−−−−−−−−−−−−−−−00∣ε21−ε200∣1−ε1ε2)\begin{pmatrix} 1 - \varepsilon_1 & \varepsilon_1 & | & 0 & 0 \\ \varepsilon_1 & 1 - \varepsilon_1 & | & 0 & 0 \\ ---&---&---&---&--- \\ 0 & 0 & | & \varepsilon_2 & 1 - \varepsilon_2 \\ 0 & 0 & | & 1 - \varepsilon_1 & \varepsilon_2 \\ \end{pmatrix} 

            graph LR
            X-->BSC1;
X-->BSC2;
BSC1-->Y;
BSC2-->Y;

C=log⁡2(2C1+2C2)ε1=0,C1=1;ε2=0.5,C2=0C=log⁡(21+20)=log⁡23>1\begin{gathered} C = \log_2 (2^{C_1} + 2^{C_2}) \\ \varepsilon_1 = 0, C_1 = 1; \varepsilon_2 = 0.5, C_2 = 0 \\ C = \log(2^1 + 2^0) = \log_2 3 > 1 \end{gathered}

选择或不选择这个信道，也是一种信息，大小1bit

连续信道的容量

  • 连续信道
    • 时间依旧连续
    • 但是取值：离散 →\rightarrow 连续
  • 引发的问题
    • 离散随机变量的互信息非负，有限
    • 取I(p,Q)I(p ,Q)最大值得到离散信道的容量
    • 连续随机变量互信息非负，但不一定有限
      • 输入输出相等，此时互信息为正无穷
    • 这样互信息的最大值为信道容量的定义就失去了意义
    • 因此我们需要一个费用的限制，在这个限制下，进行讨论

设对于连续无记忆信道{X,q(y∣x),Y}\lbrace X, q(y|x), Y\rbrace，有一个函数b(.)b(.)，称bb为x\mathbf{x}的费用。设随机矢量x=x1x2⋯xn\mathbf{x} = x_1x_2\cdots x_n的联合分布为p(x)p(x)，则平均费用为

E(b(X))≜∑xp(x)b(x)E(b(\mathbf{X})) \triangleq \sum_\mathbf{x} p(\mathbf{x})b(\mathbf{x})

连续信道的"容量-费用函数"

在费用约束的前提下，求输入输出互信息的最大值，得到容量-费用函数
设连续信道的N维联合输入输出分别为XX和YY，则其容量-费用函数定义为：

C(β)=lim⁡N→∞1Nmax⁡p(x){I(X;Y):E(b(X)≥Nβ)}C(\beta) = \lim_{N \rightarrow \infty} \frac{1}{N} \max_{p(\mathbf{x})} \lbrace I(X;Y) : E(b(X) \geq N\beta) \rbrace

可以理解为功率，在给定功率的情况下，去讨论信道的容量

加性噪声信道

Z⇓X⟶+⟶Y\begin{aligned} &Z \\ &\Downarrow \\ X \longrightarrow &+ \longrightarrow Y \end{aligned}

maxC(Ps)=max⁡I(X;Y)s.t.p(x):Ex(x2)≤Ps\begin{aligned} max &\qquad C(P_s) = \max I(X;Y) & \\ s.t. &\qquad p(x): E_x(x^2) \leq P_s \end{aligned}

q(y∣x)=Pz(y−x)=Pz(Z)q(y|x) = P_z(y - x) = P_z(Z)

当XX确定的时，YY的分布仅和ZZ的分布相关

h(Y∣X)=−∬XYPx(x)q(y∣x)log⁡q(y∣x)dxdy=−∬XYPx(X)Pz(y−x)log⁡Pz(y−x)dxdy=−∬Px(X)Pz(Z)log⁡Pz(Z)dxdz=−∫zP(Z)log⁡P(Z)dz=h(Z)\begin{aligned} h(Y|X) &= -\iint_{XY} P_x(x) q(y|x)\log q(y|x) dxdy \\ &= -\iint_{XY} P_x(X) P_z(y - x)\log P_z(y-x)dxdy \\ &= -\iint P_x(X)P_z(Z)\log P_z(Z) dxdz \\ &= -\int_z P(Z)\log P(Z)dz \\ &= h(Z) \end{aligned}

加性高斯信道

看看加性高斯信道

Z∼N(0,Pz)⇓X⟶+⟶Y\begin{aligned} &Z \sim N(0, P_z) \\ &\Downarrow \\ X \longrightarrow &+ \longrightarrow Y \end{aligned}

我们先看YY的功率，XX和ZZ相互独立

E(Y2)=E((X+Z)2)=E(X2)+E(Z2)=Ps+Ps\begin{aligned} E(Y^2) = E((X+Z)^2) = E(X^2) + E(Z^2) \\ = P_s + P_s \end{aligned}

当我们让YY取得一个正态分布，则h(Y)h(Y)可以取得最大值
也就是YY的功率在服从Ps+PsP_s + P_s的情况下，正态分布的微分熵取最大

max⁡p(x):E(X2)≤Ps=12log⁡2πe(Ps+Pz)\max_{p(x):E(X^2) \leq P_s} = \frac{1}{2}\log 2\pi e(P_s + P_z)

两个独立的正态分布，依旧是正态分布

C(Ps)=h∗(Y)−h(Z)=12log⁡2πe(Ps+Pz)−12log⁡2πe(Pz)=12log⁡Ps+PzPz=12log⁡(1+PsPz)\begin{aligned} C(P_s) &= h^*(Y) - h(Z) \\ &= \frac{1}{2}\log 2\pi e(P_s + P_z) - \frac{1}{2}\log 2\pi e(P_z) \\ &= \frac{1}{2}\log \frac{P_s + P_z}{P_z} \\ &= \frac{1}{2}\log(1 + \frac{P_s}{P_z}) \end{aligned}

PsPz\frac{P_s}{P_z}实际就是：信噪比 =信号的功率噪声的功率= \frac{\text{信号的功率}}{\text{噪声的功率}}

对于无记忆记忆加性噪声信道，若输入信号XX具有高斯分布，加性噪声功率为PnP_n，则当噪声具有高斯分布的时候，输入输出的互信息达到最小

  • 高斯噪声其实是对信道噪声最大的噪声，即相同功率下，高斯噪声使得信道容量最小
  • 高斯噪声提供最大的微分熵

一般无记忆加性噪声信道的容量

让噪声为任意分布时，无法获得信道容量的解析解，但是我们给出其上界和下界

  • 下界

C(Ps)=max⁡p(x){I(X;Y):E(X2)=Ps}≥I(XG;Y)≥I(XG;YG)=12log⁡(1+PsPN)\begin{aligned} C(P_s) &= \max_{p(x)} \lbrace I(X;Y): E(X^2) = P_s \rbrace \\ &\geq I(X_G;Y) \geq I(X_G; Y_G) = \frac{1}{2}\log(1 + \frac{P_s}{P_N}) \end{aligned}

  • 上界

E(X2)=Ps,E(Z2)=PN,E(Y2)=Ps+PNh(Y)=12log⁡(2πe(Ps+PN))C(Ps)≥12log⁡(2πe(Ps+PN))−h(Z)=12log⁡(2πePs+PNPe)Pe≜12πeexp⁡(2h(Z))\begin{aligned} E(X^2) &= P_s, \quad E(Z^2) = P_N, \quad E(Y^2) = P_s + P_N \\ h(Y) &= \frac{1}{2}\log(2\pi e(P_s + P_N)) \\ C(P_s) &\geq \frac{1}{2}\log(2\pi e(P_s + P_N)) - h(Z) \\ &= \frac{1}{2}\log(2\pi e\frac{P_s + P_N}{P_e}) \\ P_e &\triangleq \frac{1}{2\pi e}\exp(2h(Z)) \end{aligned}

并联的加性噪声信道

  • 输入：Xn,PsX_n, P_s
  • 噪声：Zn,PNZ_n, P_N
  • 在总功率限定的情况下，求信道容量-费用函数
  • 信道之间相互独立

C(Ps)=sup⁡p(X){I(X;Y):∑n=1NPsn=Ps}C(P_s) = \sup_{p(X)} \lbrace I(X;Y): \sum^N_{n=1}P_{s_n} = P_s\rbrace 

            graph LR
            X-->信道1;
X-->信道2;
X-->信道n;
信道1-->Y;
信道2-->Y;
信道n-->Y;

如何分配每一个加性高斯噪声子信道的功率，使得整体信道的功率之和达到最大值

maxI(Xn;Yn)=∑12log⁡(1+PsiPNi)s.t.∑i=1nPsi=PsPsi≥0,1≤1≤n\begin{aligned} max &\qquad I(X^n;Y^n) = \sum \frac{1}{2}\log(1 + \frac{P_{si}}{P_{Ni}}) & \\ s.t. &\qquad \sum^n_{i=1}P_{si} = P_s \\ &\qquad P_{si} \geq 0, \quad 1 \leq 1 \leq n \end{aligned}

利用拉格朗日求解的方法，对每个信道进行下列操作，λ\lambda是拉格朗日乘子

∂∂Psi[12log⁡(1+PsiPNi−λ(∑i=1nPsi−Ps))]=012PNiPSi+PNi⋅1PNi=λ=0for i≤i≤nPsi+PNi=12λλ=n2(Ps+Pn)Psi=Ps+PNn−PNifor i and Psi>0\begin{aligned} \frac{\partial}{\partial P_{si}} \Big[\frac{1}{2} \log (1 + \frac{P_{si}}{P_{Ni}} - \lambda(\sum^n_{i=1}P_{si} - P_s))\Big] &= 0 \\ \frac{1}{2} \frac{P_{Ni}}{P_{Si} + P_{Ni}} \cdot \frac{1}{P_{Ni}} = \lambda &= 0 \quad for\ i \leq i \leq n \\ P_{si} + P_{Ni} &= \frac{1}{2\lambda} \quad \lambda = \frac{n}{2(P_s + P_n)} \\ P_{si} &= \frac{P_s + P_N}{n} - P_{Ni} \quad for\ i\ and\ P_{si} > 0 \end{aligned}

当PsiP_{si}小于0，说明噪声太大，信道太糟糕，则弃之不用，再重新计算一次n−1n-1个信道，直到所有信道非负时，则完成

注水功率分配

  • 为了达到信道的容量，有些噪声很大的信道需要弃之不用

模拟信道

在时间和取值熵都连续的信道
AWGN：加性白色高斯噪声信道

  • 带宽有限：WW
  • 加性噪声：y(t)=x(t)+z(t)y(t) = x(t) + z(t)
  • 白色噪声：平稳遍历随机过程，功率谱密度均匀分布于整个频域，即功率谱密度（单位带宽噪声功率）为一个常数
  • 高斯噪声：平稳遍历随机过程，瞬时值的概率密度函数服从高斯分布

模拟信道容量

  • 输入信号：x(t)x(t)
    • 带宽有限：输入信号带宽限制在[−W,W][-W, W]内
    • 时间有限：TT
  • 输出信号：y(t)y(t)
  • 噪声信号：z(t)z(t)
    • 加性白色高斯噪声
    • 零均值
    • 两边功率谱密度：N(f)={N02∣f∣≤W0∣f∣>wN(f) = \begin{cases}\frac{N_0}{2}&|f| \leq W\\0 & |f|> w \end{cases}
    • 信道费用：输入信号的功率

莱菲斯特采样定理

信号的正交分解（信息论没有时间概念）

  • 由于信道频道首先，信号时长受限，所以，仅需要N=2WTN=2WT个采样点就可以表示
  • 因此信道再时间熵可以被离散化为2WT2WT个点，每个点上取值连续
  • 变成了并联2WT2WT个AWGN的连续信道
    • 取值连续，时间离散
  • 高斯分布独立就等于不相关
    • N个信道独立
    • 噪声功率：N0/2N_0/2

并联信道总容量费用函数：

12∑n=12WTlog⁡(1+PSnPNn)\frac{1}{2}\sum^{2WT}_{n=1} \log(1 + \frac{P_{S_n}}{P_{N_n}})

噪声约束

PNn=N02⇒PN=NPNn=2WTN02=WTN0P_{N_n} = \frac{N_0}{2} \Rightarrow P_N = NP_{N_n} = 2WT\frac{N_0}{2} = WTN_0

功率约束：（类似注水功率分配）

PSn=PsT+PNN−PNn=PsT+2WTN022WT−N02=Ps2WP_{S_n} = \frac{P_sT + P_N}{N} - P_{N_n} = \frac{P_sT + 2WT\frac{N_0}{2}}{2WT} - \frac{N_0}{2} = \frac{P_s}{2W}

香农公式

AWGN信道容量费用函数为

C=Wlog⁡(1+PsN0W)\color{red}C = W\log(1 + \frac{P_s}{N_0W})

当输入功率为：PsP_s，单位时间可以传输的信息量：CC

  • CC：bpsbps
  • WW：这个带线的信道的带宽，HzHz或s−1s^{-1}
  • PsP_s：输入信号的功率，WattWatt
  • N0N_0：带线内，噪声功率谱密度，Watt/HzWatt/Hz

提升容量的各种手段

  • 增加功率（带宽WW趋向无穷）

lim⁡W→∞C(Ps)=lim⁡W→∞PsN0log⁡2(1+PsN0W)N0WPs=PsN0log⁡2e≈1.44PsN\lim_{W \rightarrow \infty} C(P_s) = \lim_{W \rightarrow \infty} \frac{P_s}{N_0} \log_2 (1+\frac{P_s}{N_0W})^{\frac{N_0W}{P_s}} = \frac{P_s}{N_0}\log_2 e \approx 1.44 \frac{P_s}{N}

  • 增加功率（功率PsP_s趋向无穷）

lim⁡Ps→∞C(Ps)≈Wln⁡(PsN0W)\lim_{P_s \rightarrow \infty} C(P_s) \approx W \ln(\frac{P_s}{N_0W})

  • 因此，对于同样的容量的传输要求，可以采用两种方式
    • 减小带宽：发送较大功率的信号
    • 增大带宽：用较小的功率的信号传输

信息与热力学的关系

定义达到传输容量时，每比特能耗为

Eb=PsCE_b = \frac{P_s}{C}

每比特传输需要的能量与噪声谱密度有关，γ\gamma（带线范围内的信噪比）

EbN0=PsN0C=PsN0Wlog⁡(1+PsN0W)=γlog⁡(1+γ)\frac{E_b}{N_0} = \frac{P_s}{N_0C} = \frac{P_s}{N_0W\log(1 + \frac{P_s}{N_0W})} = \frac{\gamma}{\log(1 + \gamma)}

  • 信噪比γ\gamma趋于00时，上述公式取得极限值0.6930.693称为香农限
    • 香农限表示传递1bit信息所需要的最小能量
    • 热力学告诉我们N0=kTN_0 = kT
    • 所以，从物理学角度上看Ebmin=0.693kTE_{b_{min}} = 0.693kT

信道编码

对于信道(X,q(y∣x),Y)(X, q(y|x), Y)（输入字幕集，概率转移矩阵，输出字母集）的信道编码包含以下要素

  • 输入符号集合：{1,1,⋯ ,2nR}\lbrace 1, 1, \cdots, 2^{nR}\rbrace
  • 编码函数xnx^n：{1,1,⋯ ,2nR}→xn\lbrace 1, 1, \cdots, 2^{nR}\rbrace \rightarrow x^n，该函数为每一个输入符号产生了相应的信道编码码字Xn(1),Xn(2),⋯ ,Xn(m)X^n(1), X^n(2), \cdots, X^n(m)，这些码字构成的集合称为"码本"
  • 解码函数gg：Yn→{1,1,⋯ ,2nR}Y^n \rightarrow \lbrace 1, 1, \cdots, 2^{nR}\rbrace，该函数为一个确定性判决函数，它将每一个可能的接受向量映射到一个输入符号

→W消息信道编码器→Xn信道q(y∣x)→Yn信道解码器→W^消息的估计\xrightarrow{\quad W\text{消息} \quad} \text{信道编码器} \xrightarrow{\quad X^n \quad} \text{信道}_{q(y|x)} \xrightarrow{\quad Y^n \quad} \text{信道解码器} \xrightarrow{\quad \hat{W}\text{消息的估计} \quad}

信道编码的码率

(M,n)(M, n)码的码率RR定义为

R=log⁡Mn比特/传输R = \frac{\log M}{n} \text{比特/传输}

信道码的每个码字母所能携带的最大信息量

  • 通过nn次传输
  • 每次信道需要承受RR个比特的传输

称这样的信道编码为(2nR,n)(2^{nR}, n)码，这样的编码的码率为RR

信道编码的错误概率

  • 定义输入符号ii时的条件错误概率为

λi=Pr{g(Yn)≠i ∣ Xn=xn(i)}=∑ynq(yn∣xn(i))I(g(yn)≠i)\begin{aligned} \lambda_i &= Pr\lbrace g(Y^n) \neq i\ |\ X^n = x^n(i) \rbrace \\ &= \sum_{y^n}q(y^n|x^n(i)) I(g(y^n) \neq i) \end{aligned}

其中I(x)I(x)为指示函数

  • 定义(M,n)(M, n)码的最大错误概率为

λ(n)=max⁡i∈{1,2,⋯ ,M}λi\begin{aligned} \lambda^{(n)} = \max_{i \in \lbrace 1, 2, \cdots, M\rbrace} \lambda_i \end{aligned}

  • 定义(M,n)(M, n)码的算数平均错误概率为

Pe(n)=1M∑i=1MλiP^{(n)}_e = \frac{1}{M} \sum^M_{i=1}\lambda_i

  • 称一个码率RR是可达的，若存在一个信道编码(⌈2nR⌉,n)(\left \lceil 2^{nR} \right \rceil, n)，其最大差错概率在n→∞n \rightarrow \infty时趋近0
    • 这个RR就是这个信道的可达速率
    • 可达：无差错的，渐进达到的

信道的操作容量

一个信道的容量时该信道上所有可达码率的上确界，即

C=sup⁡RC = \sup R

可达：找到一个信道编解码器对，当n→∞n \rightarrow \infty，可以获得码率为RR无差错的信道传输方案

重复码

提高抗干扰能力的方法

  • 增加功率（提高信噪比）
  • 加大带宽（信号变化剧烈）
  • 延长时间（降低速率）

最直观的纠错方式就是：重复，增加冗余

误差概率关系

假定信道为二进制对称信道，出错概率为ee

→W={1,2,⋯ ,2k}Encoder→XnBSC(p)→YnDecoder→W^\xrightarrow{\quad W = \lbrace 1, 2, \cdots, 2^k \rbrace \quad} Encoder \xrightarrow{\quad X^n \quad} BSC(p) \xrightarrow{\quad Y^n \quad} Decoder \xrightarrow{\quad \hat{W} \quad}

由信息论容量CC，在所有互信息上取最大值，得到以下不等式

nC≥nI(X;Y)≥I(Xn;Yn)≥I(W;W^)=H(W)−H(W∣W^)≥k−kH(Pe)R=kn≤1−H(P)1−H(Pe)=C1−H(Pe)\begin{aligned} nC &\geq nI(X; Y) \\ &\geq I(X^n; Y^n) \\ &\geq I(W; \hat{W}) \\ &= H(W) - H(W|\hat{W}) \\ &\geq k - kH(P_e) \\ \\ R&= \frac{k}{n} \leq \frac{1 - H(P)}{1 - H(P_e)} = \frac{C}{1 - H(P_e)} \end{aligned}

通过变形

Pe=H−1(1−CR)P_e = H^{-1}(1 - \frac{C}{R})

  • 若R>CR>C，PeP_e严格大于零，代表不可能进行无差错传输，即不可能进行可靠通信
  • 若R<CR<C或R=CR=C，PeP_e可以等于0
  • 信源功率：PsP_s
  • 噪声功率：PNP_N
  • 对这个信道使用NN次，每一次都会从XX映射到YY
    • 需要求得在YY下最大个数的映射，且不同映射之间的面积不重叠

M=(Ps+PN)n(PN)n=(1+PsPN)n2\begin{aligned} M &= \frac{(\sqrt{P_s + P_N})^n}{(\sqrt{P_N})^n} \\ &= (1 + \frac{P_s}{P_N})^{\frac{n}{2}} \end{aligned}

这个数值代表我们最大能够实现的信道码率RR

R=12log⁡(1+PsPN)R = \frac{1}{2} \log(1 + \frac{P_s}{P_N})

联合典型性

设(Xn,Yn)(X^n, Y^n)是长为nn的随机序列对，其概率分布满足

p(xn,yn)=∏i=1np(xi,yi)p(x^n, y^n) = \prod^n_{i=1} p(x_i, y_i)

若(xn,yn)(x^n, y^n)满足以下条件，则称其为联合典型序列

∣−1nlog⁡p(xn)−H(X)∣<ϵ∣−1nlog⁡p(yn)−H(Y)∣<ϵ∣−1nlog⁡p(xn,yn)−H(X,Y)∣<ϵ\begin{aligned} |-\frac{1}{n}\log p(x^n) - H(X)| &< \epsilon \\ |-\frac{1}{n}\log p(y^n) - H(Y)| &< \epsilon \\ |-\frac{1}{n}\log p(x^n, y^n) - H(X, Y)| &< \epsilon \end{aligned}

联合典型序列构成的集合记为Aε(n)A^{(n)}_\varepsilon

联合渐进等同分割定理（Joint AEP）

设(Xn,Yn)(X^n, Y^n)是长度为nn的随机序列对，其分布满足

p(xn,yn)=∏i=1np(xi,yi)p(x^n, y^n) = \prod^n_{i=1} p(x_i, y_i)

则以下性质成立

  • 当n→∞n \rightarrow \infty时，Pr((Xn,Yn)∈Aε(n)→1Pr((X^n, Y^n) \in A^{(n)}_\varepsilon \rightarrow 1
  • (1−ε)2n(H(X,Y)−ε)≤∣Aε(n)∣≤2n(H(X,Y)+ε)(1 - \varepsilon)2^{n(H(X,Y)-\varepsilon)} \leq |A^{(n)}_\varepsilon| \leq 2^{n(H(X,Y)+\varepsilon)}
  • 设(X~n,Y~n)∼p(xn)p(yn)(\tilde{X}^n, \tilde{Y}^n) \sim p(x^n)p(y^n)，即X~n,Y~n\tilde{X}^n, \tilde{Y}^n统计独立且具有与p(xn,yn)p(x^n, y^n)一致的边缘分布
    • 则Pr((X~n,Y~n)∈Aϵ(n))≤2−n(I(X;Y)−3ϵ)Pr((\tilde{X}^n, \tilde{Y}^n) \in A^{(n)}_\epsilon) \leq 2^{-n(I(X;Y) - 3\epsilon)}
    • 若nn足够大，则Pr((X~n,Y~n)∈Aϵ(n))≥(1−ϵ)2−n(I(X;Y)+3ϵ)Pr((\tilde{X}^n, \tilde{Y}^n) \in A^{(n)}_\epsilon) \geq (1 - \epsilon)2^{-n(I(X;Y) + 3\epsilon)}

设随机变量X~n∼Px(xn),Y~n∼Py(yn)\tilde{X}^n \sim P_x(x^n), \tilde{Y}^n \sim P_y(y^n)相互独立

Pr((Xn,Yn)∈Aε(n))=∑(xn,yn)∈Aε(n)p(xn)p(xn)≤2n(H(X,Y)+ε)⋅2−n(H(x)−ε)⋅2−n(H(Y)−ε)=2−n(I(X;Y)−3ϵ)\begin{aligned} Pr((X^n, Y^n) \in A^{(n)}_\varepsilon) &= \sum_{(x^n, y^n) \in A^{(n)}_\varepsilon} p(x^n)p(x^n) \\ &\leq 2^{n(H(X,Y) + \varepsilon)} \cdot 2^{-n(H(x) - \varepsilon)} \cdot 2^{-n(H(Y) - \varepsilon)} \\ &= 2^{-n(I(X;Y) - 3\epsilon)} \end{aligned}

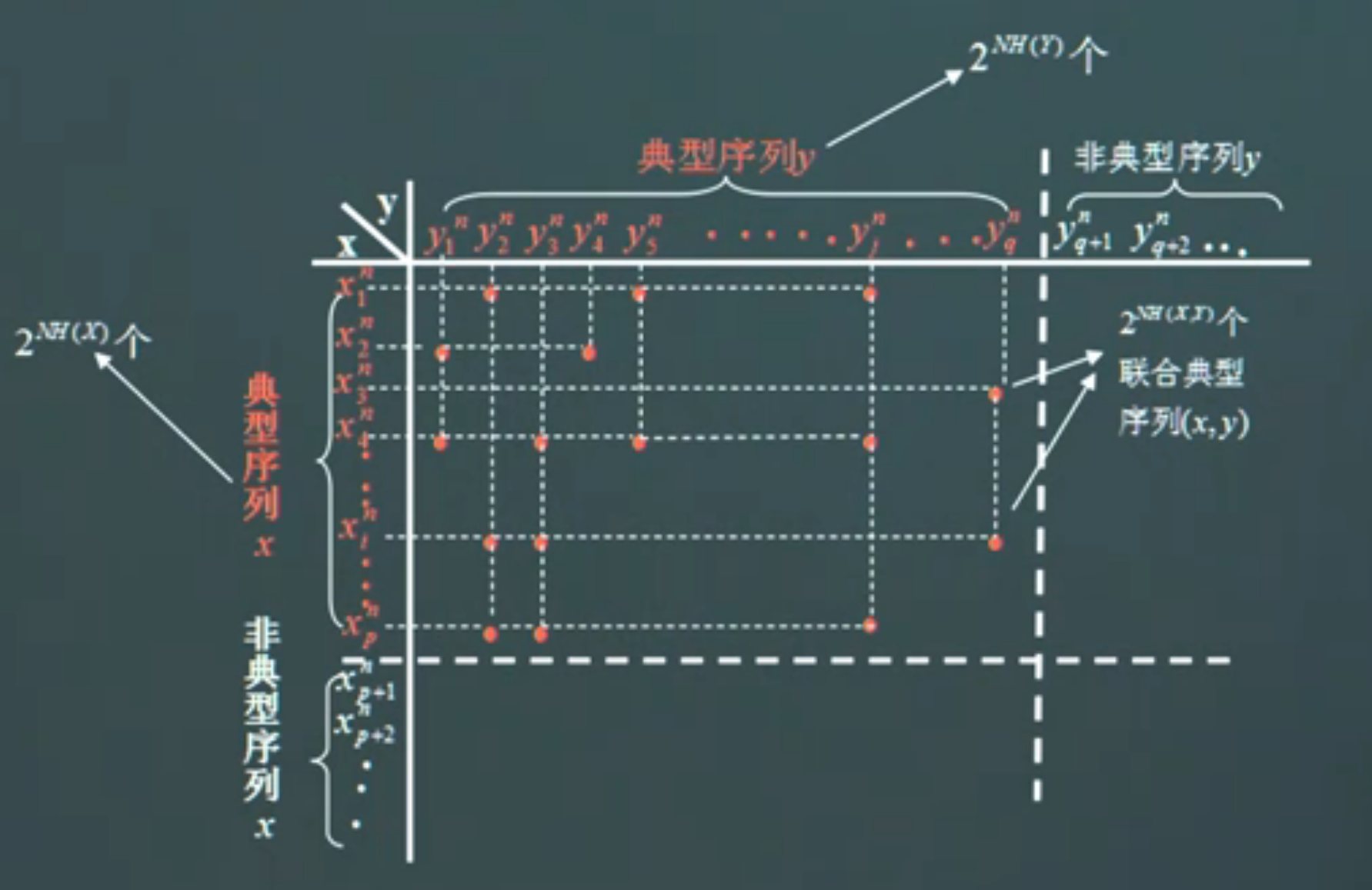
  • 联合分布中，大约有2nH(X)2^{nH(X)}个典型XX序列和2xH(Y)2^{xH(Y)}个典型YY序列
  • 其组合共有2nH(X)⋅2nH(Y)=2nH(X)+nH(Y)2^{nH(X)}\cdot 2^{nH(Y)} = 2^{nH(X)+nH(Y)}
    • 但是其中联合典型的只有2nH(X,Y)2^{nH(X,Y)}个
  • 随机选择而出现联合典型序列的概率为2−nI(X;Y)2^{-nI(X;Y)}
  • 对于典型输入序列xnx^n，存在大约2nH(Y∣X)2^{nH(Y|X)}个可能的输出，且他们等概
  • 所有可能的典型输出序列大约由2nH(Y)2^{nH(Y)}个，这些序列被分为若干个不相交的子集
  • 子集个数为2n(H(Y)−H(Y∣X))=2nI(X;Y)2^{n(H(Y) - H(Y|X))} = 2^{nI(X;Y)}，表示信道可以无误传递的最大字母序列个数

香农第二定理

  • 构造阶段
    • 假定被信道编码的消息大小为：2nR2^{nR}
    • 消息：w∈[1:2nR]w \in [1: 2^{nR}]
    • 由信道编码器，变换为Xn∼Px(x)X^n \sim P_x(x)
    • 噪声污染：q(y∣x)q(y|x)
    • 输出结果：YnY^n
    • 由信道解码器进行估计：w^\hat{w}

w∈[1:2nR]⟶Xn∼Px(x)→q(y∣x)Yn⟶w^w \in [1: 2^{nR}] \longrightarrow X^n \sim P_x(x) \xrightarrow{\quad q(y|x) \quad} Y^n \longrightarrow \hat{w}

随机编码

  • 码字生成的过程是随机的
  • 如果需要对2nR2^{nR}个字符进行编码，就要生成2nR2^{nR}个长度为nn的信道（进行编码）的输入序列

通过随机生成器，生成

e=(xn(1)xn(2)⋮xn(2nR))e = \begin{pmatrix} x^n(1) \\ x^n(2) \\ \vdots \\ x^n(2^{nR}) \end{pmatrix}

其中xn(k)x^n(k)是根据独立同分布的乘积Px(xn(k))=∏i=1nPx(xi(k))P_x(x^n(k)) = \prod^n_{i=1}P_x(x_i(k))生成出来的
这样发送字符kk，信道编码器将其查表编码为xn(k)x^n(k)，当解码器收到之后，进行判断，其方法为

如果能够找到一个k^\hat{k}，它是唯一能够使得(xn(k^),yn)∈Aε(n)(x^n(\hat{k}), y^n) \in A^{(n)}_\varepsilon联合典型的话，则k^\hat{k}为传输的符号，反之解码出错

香农第二定理-可达性证明

出错分2种

  • P(E1)P(E_1)：解码失败
  • P(E2)P(E_2)：解码重叠

P(E)=P(E1∪E2)=P(E1)+P(E2)≤ε+∑i=22nT2n(I(X;Y)−3ε)≤ε+23nε2−n(I(X;Y)−R)\begin{aligned} P(E) &= P(E_1 \cup E_2) \\ &= P(E_1) + P(E_2) \\ &\leq\varepsilon + \sum^{2^{nT}}_{i=2} 2^{n(I(X;Y) -3\varepsilon)} \\ &\leq\varepsilon + 2^{3n\varepsilon}2^{-n(I(X;Y) - R)} \end{aligned}

要使P(E)P(E)趋近于00，则需要I(X;Y)−R≥0I(X;Y) - R \geq 0，当编码为Xn∼Px∗(x)X^n \sim P^*_x(x)时，I(X;Y)=CI(X;Y) = C，不等式变为

C−R≥0R≤C\begin{aligned} C - R &\geq 0 \\ R &\leq C \end{aligned}

只要上述条件成立

P(E)→n→∞0P(E) \xrightarrow{\quad n \rightarrow \infty \quad} 0

即我们可以找到一个码率为RR的编码，当n→∞n \rightarrow \infty时，出错概率≈0\approx 0

任何一个使得错误概率趋向00的编码方案，其码率R<CR < C

nR=H(W)=H(W∣W^)+I(W;W^)=I(W;W^)≤I(Xn(W);Y)=H(Yn)−H(Yn∣Xn)≤H(Yi)−∑H(Yi∣Xi)=∑I(Xi;Yi)≤nCnR≤nC\begin{aligned} nR &= H(W) \\ &= H(W|\hat{W}) + I(W;\hat{W}) \\ &= I(W;\hat{W}) \\ &\leq I(X^n(W);Y) \\ &=H(Y^n) - H(Y^n|X^n) \\ &\leq H(Y_i) - \sum H(Y_i|X_i) \\ &=\sum I(X_i;Y_i) \\ &\leq nC \\ \\ nR \leq nC \end{aligned}

Lempel-Ziv编码

也叫做字典式压缩算法，LZ编码，其算法分为2种不同的版本

  • LZ77或滑动窗Lempel-Ziv算法
  • LZ78或树结构Lempel-Ziv算法
  • Lempel-Ziv算法的关键思想时将字符串解析成一个个词组并利用指针替换词组
  • 两种算法的区别在于各算法允许的可能匹配位置和匹配长度集合之间的差别

滑动窗Lempel-Ziv算法（LZ77）

树结构Lempel-Ziv算法（LZ78）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
abracadabrarray
a|b|r|ac|ad|ab|ra|rr|ay
(0, a)(0, b)(0, c)(1, c)(1, d)(1, b)(3, a)(3, r)(1, y)
======================================================
1  2  3  4  5  6  7  8  9
0a 0b 0c 1c 1d 1b 3a 3r 1y
======================================================
a = 00
b = 10
c = 10
d = 11
r = 000
y = 001
======================================================
00|0,10|00,10|01,10|001,11|001,10|011,000|0001,001
000100010011000111001100110000001001
  • 第k=0k = 0对的序号一定是0，所以在编码中省略
  • 编码(i,x)(i, x)对时，编码ii需要的比特数为⌈log⁡2k⌉\left \lceil \log_2 k \right \rceil，kk为第几个

汉明码

参考文献