[数理统计] - 样本及抽样分布

随机样本

总体：实验的全部可能的观察值
个体：每一个可能观察值
容量：中体中所包含的分体的个数
有限总体：容量为有限
无限总体：容量为无限

这里主要是探讨样本与总体的区别和联系等等

	总体	样本	样本观察值
期望	$\mu$	$\overline{X}$	$\overline{x}$
方差	$\sigma^2$	$S^2$	$s^2$

---

• 所谓从总体抽取一个个体，就是对总体$X$进行一次观察并记录其结果
• 在相同的条件下对总体X进行$n$次重复的独立的观察，则$n$的结果记为$X_1, X_2, \cdots, X_n$，它们相互独立
• 它们都是与$X$具有相同分布的随机变量，一组这样的数据称为来自总体$X$的一个简单随机样本

定义：设$X$是具有分布函数$F$的随机变量，若

$X_1, X_2, \cdots, X_n$

是具有同一分布函数$F$的，相互独立的随机变量，则称$X_1, X_2, \cdots, X_n$为从分布函数$F$（或总体$F$，或总体$X$）得到的容量为$n$的简单随机样本，简称样本，他们的观察值

$x_1, x_2, \cdots, x_n$

称为样本值，又称为$X$的$n$个独立的观察值

抽样方法

• 简单随机抽样
  • 放回抽样
  • 不放回抽样
• 分层抽样：按比例分层，各层取样合并
  • 每层的样本性质需要一样，不是随机
  • 精度可以提升
• 整群抽样：分集合，在群里取全部的样
  • 可以节约费用，但是精度比无作为抽样小
• 多阶段抽样：先抽几组，再在其中之一继续抽几组，以此循环到最后的单体样本
  • 节省费用，但是平均等精度会下降
• 系统抽样：标号，间隔取样

实验方法

• 随机对照实验
  • 将研究对象随机分组，对不同组实施不同的干预，在这种严格的条件下对照效果的不同
  • 在研究对象数量足够的情况下，这种方法可以抵消已知和未知的混杂因素对各组的影响
  • ===========
  • 完全随机设计
    • 是用随机化的方式来控制误差变异，认为经过随机化处理后，样本间的变异在各个处理水平上随机分布，这样就可将实验结果的差异归于不同处理的影响
    • 这种设计假设通过随机化能平衡被试间的差异，但实际上在实验结果当中常常会包括个体差异。如果我们可以将这些个体差异排除，实验结果才会更加精确
  • 随机区组设计
    • 通常是将受试对象（样本）按性质相同或相近者分成若干组，每个组中的受试对象分别随机分配到不同的处理组中去
    • 做到区组内尽量同质，使得实验结果的差异更好地归于不同处理的影响
  • 分层随机法
    • 简易的区组随机法是面向所有受试对象进行分组，只能保证将受试对象按照总体样本大小分成两组
    • 分组随机法可以实现平衡两组受试对象的生理特征
• 交叉研究
  • 将研究对象分为2组，对A组进行X实验，对B组进行Y实验，然后过一定期间，交换实验方法再进行一次
• 观察研究
  • 仅通过观察的方式收集数据，不进行任何其他干涉
• 横向研究
  • 对一个因素进行断面的调查，如：年龄
• 队列研究（纵向研究）
  • 对一群在特定时期内由共同特征的人进行调查
• 病例对照研究
  • 选出一组病例，和对照组，调查这个病的特性，如：比较患某病群体与正常人的DNS的变异程度

Fisher试验设计三原则

• 重复：评价偶然误差的大小
• 分区组：将一部分系统误差通过分组的区别去除
• 随机化：将其他意料之外的系统误差转换为偶然误差

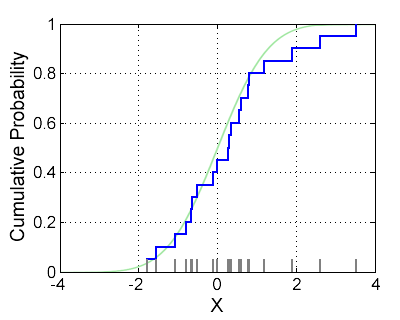
经验分布函数

又称样本分布函数，可以将其看作，以等概率$1/n$取值$X_1,X_2,\cdots,X_n$的离散型随机变量的分布函数

• 该函数的图形呈现跳跃式台阶形折现
• 如果观测值不重复，则每一跳跃为$1/n$
• 如果观测值重复，则每一跳跃为$1/n$的倍数

$F_n(x) = \frac{1}{n}S(x) = \frac{1}{n}\sum^n_{i=1}\mathbf{1}_{x_i \leq t}$

对于经验分布函数$F_n(x)$，有以下结论：对于$\forall x, n \rightarrow \infty$时，$F_n(n)$以概率$1$一致收敛于分布函数$F(x)$，即

$P(\lim_{n \rightarrow \infty} \sup_{-\infty < x < \infty} | F_n(x) - F(x) | = 0) = 1$

当$n$充分大的时候，经验分布函数的任一个观察值$F_n(x)$与总体分布函数$F(x)$只有微小的差别

抽样分布

定义：设

$X_1, X_2, \cdots, X_n$

是来自总体$X$的一个样本，

$g(X_1, X_2, \cdots, X_n)$

是$X_1, X_2, \cdots, X_n$的函数，若$g$中不含未知参数，则称$g(X_1, X_2, \cdots, X_n)$是一统计量（统计量指的是样本的函数，比如一个可以算期望值的函数E(X)），因为$X_1, X_2, \cdots, X_n$都是随机变量，所以统计量也是一个随机变量，设

$x_1, x_2, \cdots, x_n$

是相对于样本$X_1, X_2, \cdots, X_n$的样本值，则

$g(x_1, x_2, \cdots, x_n)$

是$g(X_1, X_2, \cdots, X_n)$的观察值（也就是带入函数的实际的参数）

名称	统计量	观察值
样本平均值	$\overline{X} = \frac{1}{n}\sum_{i=1}^nX_i$	$\overline{x} = \frac{1}{n}\sum_{i=1}^nx_i$
样本方差	$S^2 = \frac{1}{n-1}\sum_{i=1}^n(X_i - \overline{X})^2$	$s^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i - \overline{x})^2$
样品标准差	$S = \sqrt{S^2}$	$s = \sqrt{s^2}$
样本$k$阶原点矩	$A_k = \frac{1}{n}\sum_{i=1}^nX_i^k \quad k=1,2,\cdots$	$a_k = \frac{1}{n}\sum_{i=1}^nx_i^k \quad k=1,2,\cdots$
样本$k$阶中心距	$B_k = \frac{1}{n}\sum_{i=1}^n(X_i - \overline{X})^k \quad k=2,3,\cdots$	$b_k = \frac{1}{n}\sum_{i=1}^n(x_i - \overline{x})^k \quad k=2,3,\cdots$

统计量的分布称为抽样分布，在使用统计量机性统计推断的时候需要知道它的分布，当总体的分布函数已知时，抽样分布时确定的，打赏要求出统计量的精确分布，一般是很困难的，所以我们采用一些常用的统计量分布进行估计。

$\chi^2$分布（卡方分布）

设$X_1, X_2, \cdots, X_n$是来自总体$N(0,1)$的样本，则称统计量

$\chi^2 = X^2_1 + X^2_2 + \cdots + X^2_n$

服从自由度为$n$的$\chi^2$分布，记为$\color{red}\chi^2 \sim{} \chi^2(n)$，其中自由度为右端包含的独立变量的个数

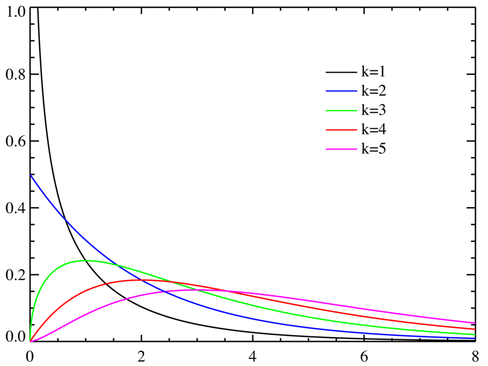
$\chi^2$分布概率密度函数

$f(y) = \begin{cases} \frac{1}{2^{n/2}\Gamma{}(n/2)}y^{n/2-1}e^{-y/2} & y > 0 \\ 0 & \text{其他} \end{cases}$

$\chi^2$分布累积分布函数

$F_k(x) = \frac{\gamma(\frac{k}{2}, \frac{x}{2})}{\frac{k}{2}}$

$\chi^2$分布的性质

• 可加性：设$\chi^2_1 \sim{} \chi^2(n_1), \chi^2_2 \sim{} \chi^2(n_2)$，并且$\chi^2_1, \chi^2_2$相互独立，则$\chi^2_1 + \chi^2_2 \sim \chi^2(n_1 + n_2)$

$\chi^2$分布的数学期望和方差

$\begin{aligned} E(\chi^2) &= n \\ D(\chi^2) &= 2n \end{aligned}$

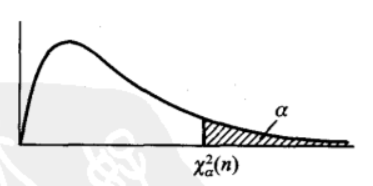
$\chi^2$分布的分位点

对于给定的正数$a$，称满足条件

$P(\chi^2 > \chi^2_a(n)) = \int_{\chi^2_a(n)}^\infty f(y)dy = a \quad a \in (0,1)$

的点$\chi^2_a(n)$为$\chi^2(n)$分布的上$a$分位点

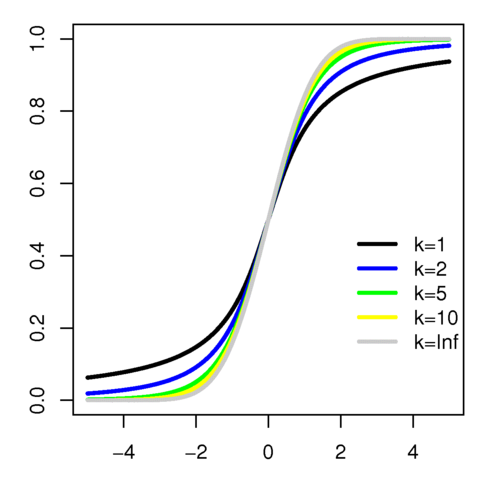
$t$分布

设$X\sim{}N(0,1), Y\sim{}\chi^2(n)$，且$X,Y$相互独立，则称随机变量

$t = \frac{X}{\sqrt{Y/n}}$

服从自由度为$n$的$t$分布，记为$t \sim{} t(n)$

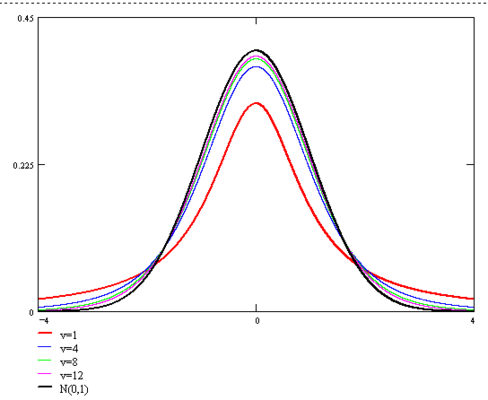
$t$分布概率密度函数

$h(t) = \frac{\Gamma[(n+1)/2]}{\sqrt{\pi n}\Gamma(n/2)}(1+\frac{t^2}{n})^{-(n+1/2)} \quad -\infty < t < \infty$

• 关于$t = 0$对称
• 当$n$充分大的时候类似于标准正态变量概率密度的图形

$\lim_{n \rightarrow \infty} h(t) = \frac{1}{\sqrt{2\pi}}e^{-t^2/2}$

$t$分布累积分布函数

$F_k(x) = \frac{1}{2} + \frac{x \Gamma((n + 1)/2)_2F_1(\frac{1}{2}, (n + 1)/2;\frac{3}{2};-\frac{x^2}{n})}{\sqrt{\pi n}\Gamma(n/2)}$

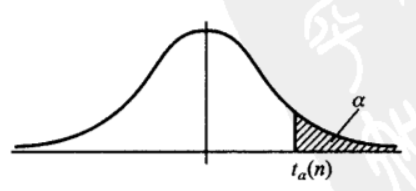
$t$分布的分位点

对于给定的正数$a$，称满足条件

$P(t > t_a(n)) = \int^\infty_{t_a(n)} h(t)dt = a, \quad a \in (0,1)$

的点$t_a(n)$为$t(n)$分布的上$a$分位点

由$t$分布上$a$分位点的定义及$h(t)$图形的对称性知

$t_{1-a}(n) = -t_a(n)$

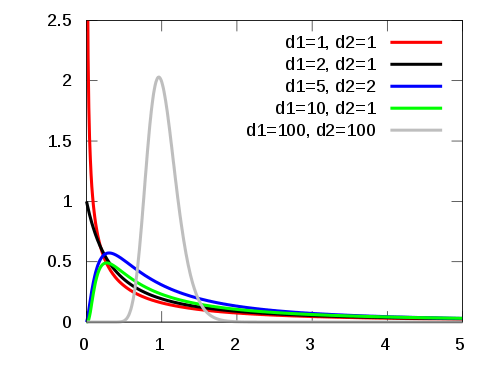
$F$分布

设$U \sim \chi^2(n_1), V \sim{} \chi^2(n_2)$，且$U, V$相互独立，则称随机变量

$F = \frac{U/n_1}{V/n_2}$

服从自由度为$(n_1, n_2)$的$F$分布，记为$\color{red}F \sim F(n_1, n_2)$

$F$分布概率密度函数

$\psi(y) = \begin{cases} \frac{\Gamma[(n_1 + n_2)/2](n_1/n_2)^{n_1/2}y^{n_1/2}-1}{\Gamma(n_1/2)\Gamma(n_2/2)[1 + (n_1y/n_2)]^{(n_1+n_2)/2}}, & y > 0 \\ 0, & \text{其他} \end{cases}$

由定义可知，若$F \sim F(n_1, n_2)$，则

$\frac{1}{F} \sim F(n_2, n_1)$

$F$分布的分位点

对于给定的$a \in (0, 1)$，满足条件

$P(F > F_a(n_1, n_2)) = \int^\infty_{F_a(n_1, n_2)}\psi(y)dy = a$

的点$F_a(n_1, n_2)$为$F(n_1, n_2)$分布上的上$a$分位点

$F$分布是上$a$分位点有如下的重要性质

$F_{\color{red}1-a\color{black}}(n_{\color{red}1\color{black}}, n_{\color{red}2\color{black}}) = \frac{1}{F_{\color{red}a\color{black}}(n_{\color{red}2\color{black}}, n_{\color{red}1\color{black}})}$

正态总体的样本均值与样本方差的分布

设总体（不管服从什么分布，只要均值和方差存在）的均值为$\mu$，方差为$\sigma^2$，$X_1, X_2, \cdots, X_n$是来自$X$的一个样本，$\overline{X}, S^2$分别是样本均值和样本方差，则

$\begin{aligned} E(\overline{X}) = \mu&, \quad D(\overline{X}) = \sigma^2/n \\ &E(S^2) = \sigma^2 \end{aligned}$

定理一：设$X_1, X_2, \cdots, X_n$是来自正态总体$N(\mu, \sigma^2)$的一个样本，$\overline{X}$是样本均值，则有

$\overline{X} \sim N(\mu, \sigma^2/n)$

定理二：设$X_1, X_2, \cdots, X_n$是来自正态总体$N(\mu, \sigma^2)$的一个样本，$\overline{X}, S^2$是样本均值和样本方差，则有

• $\frac{(n - 1)S^2}{\sigma^2} \sim \chi^2(n - 1)$
• $\overline{X}$与$S^2$相互独立

定理三：设$X_1, X_2, \cdots, X_n$是来自正态总体$N(\mu, \sigma^2)$的一个样本，$\overline{X}, S^2$是样本均值和样本方差，则有

$\frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n - 1)$

及自由度为$n-1$的$t$分布

定理四：设$X_1, X_2, \cdots, X_n$与$Y_1, Y_2, \cdots, Y_n$是来自正态总体$N(\mu_1, \sigma^2_1)$和$N(\mu_2, \sigma^2_2)$的样本，它们相互独立，$\overline{X_1}, S^2_1$和$\overline{X_2}, S^2_2$分别是样本均值和样本方差，则有

• $\frac{S^2_1/S^2_2}{\sigma^2_1/\sigma^2_2} \sim F(n_1 - 1, n_2 - 1)$
• 当$\sigma^2_1 = \sigma^2_1 = \sigma$时

$\frac{(\overline{X} - \overline{Y}) - (\mu_1 - \mu_2)}{S_w\sqrt{\frac{1}{x_1} + \frac{1}{n_2}}} \sim t(n_1 + n_2 - 2)$

其中

$S^2_w = \frac{(n_1 - 1)S^2_1 + (n_2 - 1)S^2_2}{n_1 + n_2 - 2}, \quad S_w = \sqrt{S^2_w}$

总结

	公式
样本均值，方差已知	$\overline{X} \sim N(\mu, \sigma^2/n)$
含有样本方差	$\frac{(n - 1)S^2}{\sigma^2} \sim \chi^2(n - 1)$
含有样本均值	$\frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n - 1)$
2个样本	$\frac{S^2_1/S^2_2}{\sigma^2_1/\sigma^2_2} \sim F(n_1 - 1, n_2 - 1)$

这里的分布主要供接下来的置信区间，假设检验使用

分布的特点：

• $t$分布：对称性
• $F$分布：$F_{1-a}(n_1, n_2) = \frac{1}{F_a(n_1, n_2)}$