huhu's Blog

FLOWER ON THE PRECIPICE

[数理统计] - 参数估计

发表于 更新于 分类于
本文字数： 14k 阅读时长 ≈ 13 分钟

点估计

设总体XX的分布函数的形式已知，但它的一个或多个参数未知，借助于总体XX的一个样本来估计总体未知参数的值的问题称为参数的点估计问题

点估计问题的一般提法如下：设

名称 值
总体XX的分布函数 F(x;θ)F(x; \theta)
XX的一个样本 X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n
相应的一个样本值 x1,x2,⋯ ,xnx_1, x_2, \cdots, x_n

点估计问题就是要构造一个适当的统计量

θ^(X1,X2,⋯ ,Xn)\hat{\theta}(X_1, X_2, \cdots, X_n)

同它的客观值

θ^(x1,x2,⋯ ,xn)\hat{\theta}(x_1, x_2, \cdots, x_n)

作为未知参数θ\theta的近似值，我们称θ^(X1,X2,⋯ ,Xn)\hat{\theta}(X_1, X_2, \cdots, X_n)为θ\theta的估计量，称θ^(x1,x2,⋯ ,xn)\hat{\theta}(x_1, x_2, \cdots, x_n)为θ\theta的估计值

一般，我们有2种点估计的方法

矩估计法

设XX为连续型随机变量，其概率密度为

f(x;θ1,θ2,⋯ ,θn)f(x; \theta_1, \theta_2, \cdots, \theta_n)

或XX为离散型随机变量，其分布律为

P(X=x)=p(x;θ1,θ2,⋯ ,θn)P(X=x) = p(x;\theta_1, \theta_2, \cdots, \theta_n)

其中θ1,θ2,⋯ ,θn\theta_1, \theta_2, \cdots, \theta_n为待估计参数，X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n是来自XX的样本，假设总体XX的前kk 阶矩

{μ1=E(Xl)=∫∞∞xlf(x;θ1,θ2,⋯ ,θn)dx连续型μ1=E(Xl)=∑x∈RXxlf(x;θ1,θ2,⋯ ,θn)离散型\begin{cases} \mu_1 &= E(X^l) = \int^\infty_\infty x^lf(x; \theta_1, \theta_2, \cdots, \theta_n)dx & \text{连续型} \\ \mu_1 &= E(X^l) = \sum_{x \in R_X} x^lf(x; \theta_1, \theta_2, \cdots, \theta_n) & \text{离散型} \end{cases}

其中RXR_X是XX可能取值的范围，一般来说，他们是θ1,θ2,⋯ ,θn\theta_1, \theta_2, \cdots, \theta_n的函数，

  • 基于样本矩依概率收敛与相应的总体矩μ1(l=1,2,⋯ ,k)\mu_1(l = 1,2,\cdots,k)
  • 样本矩的连续函数以概率收敛于相应的总体矩的连续函数

Al=1n∑i=1nXilA_l = \frac{1}{n}\sum_{i=1}^nX^l_i

  • 就用样本矩作为相应的总体矩的估计量，
  • 样本矩的连续函数作为相应的总体矩的连续函数的估计量

这种估计方法就是矩估计法

矩估计法的具体做法

待续

最大近然估计法

的目：就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值

  • 所有样本都是独立的，且相同分布

设X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n是来自XX的样本，则X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n的联合分布律

∏i=1np(xi,θ)\prod^n_{i=1}p(x_i, \theta)

记x1,x2,⋯ ,xnx_1, x_2, \cdots, x_n是样本X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n的样本值，则取到这样一组观察值的概率为

f(x1∣θ)×f(x2∣θ)×⋯×f(xn∣θ)=∏i=1np(xi,θ)f(x_1|\theta) \times f(x_2|\theta) \times \cdots \times f(x_n|\theta) = \prod^n_{i=1}p(x_i, \theta)

记为L(θ)L(\theta)，称作似然函数（这实际是个常数，一个概率）

  • 因为是从样本观察值反推总体，x1,x2,⋯ ,xnx_1, x_2, \cdots, x_n都是已知的常数
  • 我们取到了x1,x2,⋯ ,xnx_1, x_2, \cdots, x_n这样一组样本值，表明取到的概率L(θ)L(\theta)较大
  • 对于θ\theta可取的值里，如果θ0\theta_0使得L(θ)L(\theta)取得最大值，我们就只考虑这个θ0\theta_0
  • 在θ\theta可取的值Θ\Theta里，挑选一个使似然函数L(θ)L(\theta)达到最大的参数值θ^\hat{\theta}，作为参数θ\theta的估计值

L(θ^)=max⁡θ∈ΘL(θ)L(\hat{\theta}) = \max_{\theta \in \Theta} L(\theta)

  • 最大似然估计值：θ^\hat{\theta}与x1,x2,⋯ ,xnx_1, x_2, \cdots, x_n有关，从而记为θ^(x1,x2,⋯ ,xn)\hat{\theta}(x_1, x_2, \cdots, x_n)
  • 最大似然估计量：θ^(X1,X2,⋯ ,Xn)\hat{\theta}(X_1, X_2, \cdots, X_n)

似然函数

对于离散型和连续型随机变量，极大似然估计值θ^\hat{\theta}都满足：

L(θ^)=max⁡L(θ)L(\hat{\theta}) = \max L(\theta)

  • 离散型随机变量：L(θ)=∏i=1NP(xi)L(\theta) = \prod^N_{i=1}P(x_i)
  • 连续型随机变量：L(θ)=∏i=1Nf(xi)L(\theta) = \prod^N_{i=1}f(x_i)

确定最大似然估计量

通过上面的似然函数，可以把确定最大似然估计量的问题转化为微积分中求最大值的问题
在很多情况下，p(x:θ)p(x:\theta)和f(x:θ)f(x:\theta)关于θ\theta可微

ddθL(θ)\frac{d}{d\theta}L(\theta)

解得，又因L(θ)L(\theta)与ln⁡L(θ)\ln{L(\theta)}在同一个θ\theta的地方取得极值，因此，θ\theta的最大似然估计θ\theta可以从方程

ddθln⁡L(θ)=0\frac{d}{d\theta}\ln L(\theta) = 0

求出，称为对数似然方程

一般来说，确定最大似然估计量分为4个步骤

step1. 确定分布律/分布函数PP
step2. 计算L(p)=∏i=inPL(p) = \prod^n_{i=i}P
step3. 计算ln⁡L(p)\ln{L(p)}
step4. 计算ddpln⁡L(p)=0\frac{d}{dp}\ln L(p) = 0，解出pp

估计量的评选标准

对于用不同估计方法求出的估计量，我们希望知道采用哪一个估计量更好，对此，我们有3个性质来确定

无偏性

设X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n时总体XX的一个样本，θ∈Θ\theta \in \Theta时包含在总体XX的分布中的待估参数，Θ\Theta是θ\theta的取值范围

无偏性：若估计量θ^=θ^(X1,X2,⋯ ,Xn)\hat{\theta} = \hat{\theta}(X_1, X_2, \cdots, X_n)的数学期望E(θ^)E(\hat{\theta})存在，且∀θ∈Θ\forall \theta \in \Theta有

E(θ^)=θE(\hat{\theta}) = \theta

则称θ^\hat{\theta}是θ\theta的无偏估计量

无偏性：估计量可能偏大偏小，反复将这一估计量使用多次，就"平均"来说其偏差为零

无论总体服从什么分布

  • 样本均值X‾\overline{X}是总体均值μ\mu的无偏估计
  • 样本方差S2=1n−1∑i=1n(XI−X‾)2S^2=\frac{1}{n-1}\sum^n_{i=1}(X_I-\overline{X})^2是总体方差的无偏估计

有效性

假设有θ^1\hat{\theta}_1和θ^2\hat{\theta}_2两个估计量，如果θ^1\hat{\theta}_1的观察值较θ^2\hat{\theta}_2更密集在真值θ\theta的附加，则认为θ^1\hat{\theta}_1较θ^2\hat{\theta}_2为理想

有效性：设θ^1=θ^1(X1,X2,⋯ ,Xn)\hat{\theta}_1 = \hat{\theta}_1(X_1, X_2, \cdots, X_n)与θ^2=θ^2(X1,X2,⋯ ,Xn)\hat{\theta}_2 = \hat{\theta}_2(X_1, X_2, \cdots, X_n)都是θ\theta的无偏估计量，若∀θ∈Θ\forall \theta \in \Theta，有

D(θ^1)≤D(θ^)2D(\hat{\theta}_1) \leq D(\hat{\theta})_2

且至少对于某一个θ∈Θ\theta \in \Theta上式成立，则称θ^1\hat{\theta}_1较θ^2\hat{\theta}_2有效

相合性

假设样本容量不固定，我们希望估计量随着样本容量的增大，其值稳定于待估参数的真值。

相合性：设θ^=θ^(X1,X2,⋯ ,Xn)\hat{\theta} = \hat{\theta}(X_1, X_2, \cdots, X_n)为参数θ\theta的估计量，若对于任意θ∈Θ\theta \in \Theta，当n→∞n \rightarrow \infty时θ^(X1,X2,⋯ ,Xn)\hat{\theta}(X_1, X_2, \cdots, X_n)依概率收敛于θ\theta，则称θ^\hat{\theta}为θ\theta的相合估计量

lim⁡n→∞P(∣θ^−θ∣<ε)=1.∀ε>0\lim_{n \rightarrow \infty}P(|\hat{\theta} - \theta| < \varepsilon) = 1. \quad \forall\varepsilon > 0

区间估计

对于一个未知量，我们在测量或者计算的时候，还需要估计它的误差，需要知道真值所在的范围，类似的，对于未知参数θ\theta除了求出它的点估计θ^\hat{\theta}外，我们还希望求出一个范围，并且知道这个范围包含参数θ\theta真值的可信程度，这样的范围称为区间估计

置信区间

设总体XX的分布函数F(x:θ)F(x:\theta)含有一个未知参数θ\theta，对于给定值a,a∈(0,1)a, a \in (0,1)，若来自XX的样本

X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n

确定的两个统计量θ‾<θ‾\underline{\theta} < \overline{\theta}

θ‾=θ‾(X1,X2,⋯ ,Xn)θ‾=θ‾(X1,X2,⋯ ,Xn)\begin{aligned} \overline{\theta} &= \overline{\theta}(X_1, X_2, \cdots, X_n) \\ \underline{\theta} &= \underline{\theta}(X_1, X_2, \cdots, X_n) \end{aligned}

对于任意θ\theta满足

P(θ‾<θ<θ‾)≥1−aP(\underline{\theta} < \theta < \overline{\theta}) \geq 1 - a

则称随机区间

(θ‾,θ‾)(\underline{\theta}, \overline{\theta})

是θ\theta的置信水平为1−a1-a的置信区间，θ‾\underline{\theta}和θ‾\overline{\theta}分别称为置信水平为1−a1-a的双侧置信区间的置信下限和置信上限，1−a1-a称为置信水平。（这里的aa不是假设检验里面aa）

对于XX是连续型随机变量时，对于给定的aa，我们可以求出置信区间
但是当XX是离散型随机变量时，对于给定的aa，常常找不到一个区间使得置信区间恰好为1−a1-a，此时我们需要找置信区间至少为1−a1-a且尽可能的接近。

设总体X∼N(μ,σ2)X \sim{} N(\mu, \sigma^2)，σ2\sigma^2为已知，μ\mu为未知，设

X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n

是来自XX的样本，求μ\mu的置信水平为1−a1-a的置信区间。

解：我们知道X‾\overline{X}是μ\mu的无偏估计，且

X‾−μσ/n∼N(0,1)\frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim{} N(0, 1)

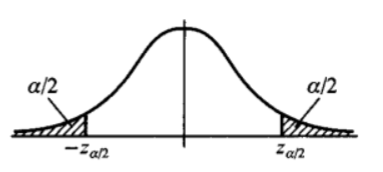
X‾−μσ/n\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}所服从的分布N(0,1)N(0,1)不依赖于任何未知参数，按照标准正态分布的上aa分位点的定义，有

P(∣X‾−μσ/n∣<za/2)=1−aP(|\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}| < z_{a/2}) = 1 - a

也就是

P(∣X‾−σnza/2∣<μ<∣X‾+σnza/2∣)=1−aP(|\overline{X} - \frac{\sigma}{\sqrt{n}}z_{a/2}| < \mu < |\overline{X} + \frac{\sigma}{\sqrt{n}}z_{a/2}|) = 1 - a

于是就有了μ\mu的这么一个置信水平为1−a1-a的置信区间

(X‾−σnza/2,X‾+σnza/2)(\overline{X} - \frac{\sigma}{\sqrt{n}}z_{a/2},\quad \overline{X} + \frac{\sigma}{\sqrt{n}}z_{a/2})

例子：取1−a=0.951-a=0.95，σ=1,n=16\sigma = 1, n = 16，得za/2=z0.025=1.96z_{a/2} = z_{0.025} = 1.96，那么区间就是

(X‾−116×1.96,X‾+116×1.96)(\overline{X} - \frac{1}{\sqrt{16}}\times1.96, \quad \overline{X} + \frac{1}{\sqrt{16}}\times1.96)

其含义为：μ\mu的真值在区间(X‾−1161.96,X‾+1161.96)(\overline{X} - \frac{1}{\sqrt{16}}1.96, \overline{X} + \frac{1}{\sqrt{16}}1.96)的概率是95%95\%

双侧置信区间

正态总体均值与方差的区间估计

单个总体

总体：N(μ,σ2)N(\mu, \sigma^2)
样本：X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n
置信水平：1−a1 - a
样本均值，方差：X‾,S2\overline{X}, S^2

单个总体均值的置信区间

σ2\sigma^2已知，采用枢轴量X‾−μS/n\frac{\overline{X} - \mu}{S/\sqrt{n}}，则置信区间为：(X‾±σnza/2)(\overline{X} \pm \frac{\sigma}{\sqrt{n}}z_{a/2})

σ2\sigma^2未知，利用σ2\sigma^2的无偏估计S2S^2，利用抽样分布的定理X‾−μS/n∼t(n−1)\frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n - 1)，这里t(n−1)t(n - 1)分布不依赖其他任何未知参数，即可得

P(−ta/2(n−1)<X‾−μS/n<ta/2(n−1))=1−aP(-t_{a/2}(n-1) < \frac{\overline{X} - \mu}{S/\sqrt{n}} < t_{a/2}(n-1)) = 1 - a

化简可得

P(X‾−Snta/2(n−1)<μ<X‾+Snta/2(n−1))P(\overline{X} - \frac{S}{\sqrt{n}}t_{a/2}(n-1) < \mu < \overline{X} + \frac{S}{\sqrt{n}}t_{a/2}(n-1))

得到μ\mu的这么一个置信水平为1−a1-a的置信区间

(X‾±Snta/2(n−1))(\overline{X} \pm \frac{S}{\sqrt{n}}t_{a/2}(n-1))

单个总体方差的置信区间

μ2\mu^2未知，利用σ2\sigma^2的无偏估计S2S^2，利用抽样分布的定理(n−1)S2σ2∼χ2(n−1)\frac{(n - 1)S^2}{\sigma^2} \sim \chi^2(n - 1)，这里χ2(n−1)\chi^2(n - 1)分布不依赖其他任何未知参数，枢轴量为(n−1)S2σ2\frac{(n - 1)S^2}{\sigma^2}，即可得

P(χ1−a/22(n−1)<(n−1)S2σ2<χa/22(n−1))=1−aP(\chi^2_{1-a/2}(n - 1) < \frac{(n - 1)S^2}{\sigma^2} < \chi^2_{a/2}(n - 1)) = 1 - a

化简可得

P((n−1)S2χa/22(n−1)<σ2<(n−1)S2χ1−a/22(n−1))P(\frac{(n-1)S^2}{\chi^2_{a/2}(n-1)} < \sigma^2 < \frac{(n-1)S^2}{\chi^2_{1 - a/2}(n-1)})

得到σ2\sigma^2的这么一个置信水平为1−a1-a的置信区间

((n−1)S2χa/22(n−1),(n−1)S2χ1−a/22(n−1))(\frac{(n-1)S^2}{\chi^2_{a/2}(n-1)}, \frac{(n-1)S^2}{\chi^2_{1 - a/2}(n-1)})

单个总体置信区间总结
            graph TD
            是求均值还是方差置信区间 --均值--> 方差是否已知;
是求均值还是方差置信区间 --方差--> 均值是否已知;
方差是否已知 --以知--> 正态分布;
方差是否已知 --未知--> t分布;
均值是否已知 --未知--> x分布;

两个总体

总体：N(μ1,σ12),N(μ2,σ22)N(\mu_1, \sigma^2_1), N(\mu_2, \sigma^2_2)
样本：X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n和Y1,Y2,⋯ ,YnY_1, Y_2, \cdots, Y_n
置信水平：1−a1 - a
样本均值，方差：X‾,S12\overline{X}, S^2_1和Y‾,S22\overline{Y}, S^2_2

两个总体方差均值之差的置信区间

σ12,σ22\sigma^2_1, \sigma^2_2已知，因X‾,Y‾\overline{X}, \overline{Y}分别为μ1,μ2\mu_1, \mu_2的无偏估计，所以X‾−Y‾\overline{X} - \overline{Y}是μ1−μ2\mu_1 - \mu_2的无偏估计，根据X‾,Y‾\overline{X}, \overline{Y}的独立性，计算出期望和方差，按照单个总体的的步骤，得

X‾−Y‾∼N(μ1−μ2,σ12n1+σ22n2)\overline{X} - \overline{Y} \sim N(\mu_1 - \mu_2, \frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2})

进行标准化

(X‾−Y‾)−(μ1−μ2)σ12n1+σ22n2∼N(0,1)\frac{(\overline{X} - \overline{Y}) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}}} \sim N(0, 1)

取(X‾−Y‾)−(μ1−μ2)σ12n1+σ22n2\frac{(\overline{X} - \overline{Y}) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}}}作为枢轴量，得到u1−u2u_1 - u_2的置信水平1−a1-a置信区间

(X‾−Y‾±za/2σ12n1+σ22n2)(\overline{X} - \overline{Y} \pm z_{a/2}\sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}})

σ12=σ22=σ2\sigma^2_1 = \sigma^2_2 = \sigma^2，但是σ2\sigma^2未知，利用抽样分布的定理X‾−μS/n∼t(n−1)\frac{\overline{X} - \mu}{S/\sqrt{n}} \sim t(n - 1)，这里t(n−1)t(n - 1)分布不依赖其他任何未知参数，即可得

(X‾−Y‾)−(μ1−μ2)Sw1n1+1n2∼t(n1+n2−2)\frac{(\overline{X} - \overline{Y}) - (\mu_1 - \mu_2)}{S_w\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t(n_1 + n_2 - 2)

取(X‾−Y‾)−(μ1−μ2)Sw1n1+1n2\frac{(\overline{X} - \overline{Y}) - (\mu_1 - \mu_2)}{S_w\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}作为枢轴量，得到u1−u2u_1 - u_2的置信水平1−a1-a置信区间

(X‾−Y‾±ta/2(n1+n2−2)Sw1n1+1n2)(\overline{X} - \overline{Y} \pm t_{a/2}(n_1 + n_2 - 2)S_w\sqrt{\frac{1}{n_1} + \frac{1}{n_2}})

这里

Sw2=(n1−1)S12+(n2−1)S22n1+n2−2,Sw=Sw2S^2_w = \frac{(n_1 - 1)S^2_1 + (n_2 - 1)S^2_2}{n_1 + n_2 - 2}, \quad S_w = \sqrt{S^2_w}

两个总体方差方差之比的置信区间

μ1,μ2\mu_1, \mu_2未知，利用σ2\sigma^2的无偏估计S2S^2，利用抽样分布的定理S12/S22σ12/σ22∼F(n1−1,n2−1)\frac{S^2_1/S^2_2}{\sigma^2_1/\sigma^2_2} \sim F(n_1 - 1, n_2 - 1)，这里F(n1−1,n2−1)F(n_1 - 1, n_2 - 1)分布不依赖其他任何未知参数，枢轴量为S12/S22σ12/σ22\frac{S^2_1/S^2_2}{\sigma^2_1/\sigma^2_2}，即可得

P(F1−a/2(n1−1,n2−1)<S12/S22σ12/σ22<Fa/2(n1−1,n2−1))=1−aP(F_{1-a/2}(n_1 - 1, n_2 - 1) < \frac{S^2_1/S^2_2}{\sigma^2_1/\sigma^2_2} < F_{a/2}(n_1 - 1, n_2 - 1)) = 1 - a

即

P(S12S221Fa/2(n1−1,n2−1)<σ12σ22<S12S221F1−a/2(n1−1,n2−1))=1−aP(\frac{S^2_1}{S^2_2}\frac{1}{F_{a/2}(n_1 - 1, n_2 - 1)} < \frac{\sigma^2_1}{\sigma^2_2} < \frac{S^2_1}{S^2_2}\frac{1}{F_{1 - a/2}(n_1 - 1, n_2 - 1)}) = 1 - a

得到σ12/σ22\sigma^2_1/\sigma^2_2的这么一个置信水平为1−a1-a的置信区间

(S12S221Fa/2(n1−1,n2−1),S12S221F1−a/2(n1−1,n2−1))(\frac{S^2_1}{S^2_2}\frac{1}{F_{a/2}(n_1 - 1, n_2 - 1)}, \frac{S^2_1}{S^2_2}\frac{1}{F_{1 - a/2}(n_1 - 1, n_2 - 1)})

两个总体置信区间总结
            graph TD
            是求均值还是方差置信区间 --均值--> 方差是否已知;
是求均值还是方差置信区间 --方差--> 均值是否已知;
方差是否已知 --以知--> 正态分布;
方差是否已知 --未知,但相等--> t分布;
均值是否已知 --未知--> f分布;

单侧置信区间

在上面，对于未知参数θ\theta，我们给出22个统计量θ‾,θ‾\underline{\theta}, \overline{\theta}，得到θ\theta的双侧置信区间(θ‾,θ‾)(\underline{\theta}, \overline{\theta})，但是在某些实际问题中，我们关心的只是θ\theta的下限或上限，于是就有了单侧置信区间

对于给定值a,a∈(0,1)a, a \in (0,1)，若来自XX的样本

X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n

确定的统计量θ‾\underline{\theta}，对于任意θ\theta满足

P(θ‾<θ)≥1−aP(\underline{\theta} < \theta) \geq 1 - a

称随机区间(θ‾,∞)(\underline{\theta}, \infty)是θ\theta的置信水平为1−a1-a的单侧置信区间，θ‾\underline{\theta}称为θ\theta的置信水平为1−a1-a的单侧置信下限

若统计量θ‾\underline{\theta}，对于任意θ\theta满足

P(θ<θ‾)≤1−aP(\theta < \overline{\theta}) \leq 1 - a

称随机区间(−∞,θ‾)(-\infty, \overline{\theta})是θ\theta的置信水平为1−a1-a的单侧置信区间，θ‾\overline{\theta}称为θ\theta的置信水平为1−a1-a的单侧置信上限

0-1分布参数的区间估计

设样本来自X∼0−1(p)X \sim 0-1(p)分布的总体XX，XX的分布律为

f(x;p)=px(1−p)1−x,x=0,1f(x; p) = p^x(1 - p)^{1 - x}, \quad x = 0, 1

pp为未知参数，求pp的置信水平为1−a1-a的置信区间

  • 均值：u=pu = p
  • 方差：σ2=p(1−p)\sigma^2 = p(1-p)

设X1,X2,⋯ ,XnX_1, X_2, \cdots, X_n是一个样本，由中心极限定理知

∑i=1nXi−npnp(1−p)=xX‾−npnp(1−p)\frac{\sum^n_{i=1}X_i - np}{\sqrt{np(1-p)}} = \frac{x\overline{X} - np}{\sqrt{np(1-p)}}

近似的服从正态分布，于是可以得到

P(−za/2<xX‾−npnp(1−p)<za/2)≈1−aP(-z_{a/2} < \frac{x\overline{X} - np}{\sqrt{np(1-p)}} < z_{a/2}) \approx 1 - a

不等式等价于

(n+za/22)p2−(2nX‾+za/22)p+nX‾2<0(n + z^2_{a/2})p^2 - (2n\overline{X} + z^2_{a/2})p + n\overline{X}^2 < 0

得区间为

(12a(−b−b2−4ac),12a(−b+b2−4ac))(\frac{1}{2a}(-b-\sqrt{b^2 - 4ac}),\quad \frac{1}{2a}(-b+\sqrt{b^2 - 4ac}))

{a=n+za/22b=−(2nX‾+za/22)\begin{cases} a = n + z^2_{a/2} \\ b = -(2n\overline{X}+z^2_{a/2}) \end{cases}