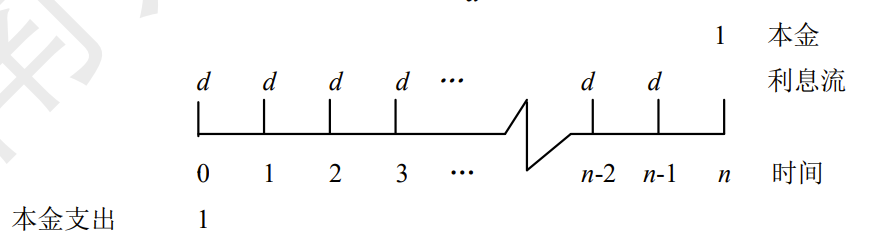[学习笔记] - 利息理论

金钱具有孳生繁衍性。金钱可以产生金钱

基本概念

$a(t)$ $a (t)$ : 一单位本金在时刻 $t$ $t$ 的积累值
- $a(0) = 1$
$A(t)$ $A (t)$ : $K$ $K$ 单位本金在时刻 $t$ $t$ 的积累值
- $A(t) = K \times a(t)$
- $A(0) = K$
贴现函数: $a^{-1}(t)$ $a^{- 1} (t)$
- $t$ 时的1元钱在0时的限值
- 记为： $v$

a^{-1}(t) = \frac{1}{a(t)}, a(t) = \frac{1}{a^{-1}(t)}

金钱具有时间价值

$I$ : 利息
$I_n$ : 某项投资从投资日起第 $n$ 个度量期所赚得的利息金额
$P$ : 投资本金

\begin{aligned} I_n &= A(n) - A(n-1) \\ &= P \times a(n) - P \times a(n-1) \\ &= P \times [a(n) - a(n-1)] \\ \\ I &= A(n) - A(0) \\ &= P \times a(n) - P \times a(0) \\ &= P \times [a(n) - 1] \\ &= I_1 + I_2 + \cdots + I_n \end{aligned}

$I$ : 表示的是在一段时期上所得到的利息的量
$a(t)$ : 表示的是在某一时间点的积累量

利率

\begin{aligned} \text{利息} = \frac{\text{利息}}{\text{本金}} \end{aligned}

实质利率

$i$ : 该度量期内得到的利息与此度量期开始时的本金金额之比

\begin{aligned} i &= \frac{I_1}{A(0)} \\ &= \frac{P \times a(1) - P}{P} \\ &= a(1) - 1 \\ \\ i_n &= \frac{I_n}{A(n - 1)} \\ &= \frac{P \times a(n) - P \times a(n - 1)}{P \times a(n - 1)} \\ &= \frac{I_n}{P \times a(n - 1)} \end{aligned}

单利

$a(t) = 1 + it$

\begin{aligned} i_n &= \frac{a(n) - a(n - 1)}{a(n - 1)} \\ &= \frac{(1 + in) - [1 + i(n - 1)]}{1 + i(n - 1)} \\ &= \frac{i}{1 + i(n - 1)} \end{aligned}

常数的单利意味着递减的实质利率

复利

$a(t) = (1 + i)^t$

\begin{aligned} I_n &= a(n) - a(n - 1) \\ &= (1 + i)^n - (1 + i)^{n-1} \\ &= ia(n - 1) \\ i_n &= \frac{a(n) - a(n - 1)}{a(n - 1)} \\ &= \frac{I_n}{a(n - 1)} \\ &= i \end{aligned}

常数的复利意味着常数的实质利率
对比单利，复利的增长

\begin{aligned} a(t + \Delta t) - a(t) &= \Delta t i \\ \frac{a(t + \Delta t) - a(t)}{a(t)} &= (1 + i)^{\Delta t} - 1 (\text{与$t$无关}) \end{aligned}

实质贴现率

$d$ : 该度量期内产生的利息金额与期末的累积值之比

\begin{aligned} d &= \frac{P \times a(1) - P}{A(1)} \\ &= \frac{I_1}{P \times a(1)} \end{aligned}

实质利率：对期末支付的利息的度量
实质贴现率：对期初支付的利息的度量

\begin{aligned} d_n &= \frac{P \times a(n) - P \times a(n - 1)}{A(n)} \\ &= \frac{I_n}{P \times a(n)} \\ &= \frac{\text{第n期的利息}}{\text{第n期的累积值}} \end{aligned}

复贴现

\begin{aligned} a^{-1}(t) &= \frac{1}{a(t)} = \frac{1}{(1 + i)^t} = (1 - d)^t \\ a^{-1}(1) &= v(\text{贴现值}) = 1 - d \\ \downarrow \\ a^{-1}(t) &= v^t \end{aligned}

与实质利率 $i$ 等价的实质贴现率为 $1/(1+i)$
若以贴现率 $d$ 借款，则实际得到 $1 - d$ ，支付利息为 $d$

i = \frac{d}{1 - d} \\ \downarrow \\ \begin{aligned} d &= \frac{i}{1 + i} = iv = i(1 - d) \\ d &= 1 - \frac{1}{1 + i} = 1 - v \\ &\downarrow \\ &i - d = id \end{aligned}

某人可以借款1而在期末还 $1 + i$
某人可以借款 $1 - d$ 而在期末还 $1$
本金差为 $d$ ，利息差为 $id$
实际上两种选择的利息差为 $i - d$

单利贴现： $a^{-1}(t) = 1 - dt$

名义利率·贴现率

实际问题中，往往有很多在一个度量期中利息支付不止一次或者在多个度量期利息才支付一次的情形。

$i^{(m)}$ $i^{(m)}$ ：每一时期付 $m$ $m$ 次利息的名义利率
- 每 $1/m$ 个度量期支付利息一次，每 $1/m$ 个度量期上的实质利率为 $i^{(m)}/m$

名义利率 $i^{(m)}$ ，是指每 $1/m$ 个度量期支付利息一次，而在每 $1/m$ 个度量期上的实质利率为 $i^{(m)}/m$ , 若一年为一个度量期， $i^{(4)}$ 的名义利率指的是每季度的实质利率为2%，称作每年计息4次的年名义利率为8%或季度转换名义利率为8%

\begin{aligned} \text{名义利率} &= \text{周期利率} \times \text{计息周期数} \\ \text{有效利率} &= \frac{\text{一年内按复利计算得到的利息}}{\text{本金}} \end{aligned}

为了方便计算

\begin{aligned} \frac{\text{按复利计算的本利和}-\text{本金}}{\text{本金}} &= \text{有效利率} \\ \text{按复利计算的本利和} &= \text{本金}\times(1+\text{利率})^n \\ &\downarrow \\ \frac{\text{本金}\times(1+\text{周期利率})^{\text{计息周期数}} - \text{本金}}{\text{本金}} &= \text{有效利率} \\ (1 + \text{周期利率})^{\text{计息周期数}} - 1 &= \text{有效利率} \\ (1 + \frac{i^{(m)}}{m})^m - 1 &= i \end{aligned}

日本情况

実質年率：有效利率

金利：名义利率

金利/12 = 周期利率

\begin{aligned} 1 + i &= (1 + \frac{i^{(m)}}{m})^m \\ &\downarrow \\ i &= (1 + \frac{i^{(m)}}{m})^m - 1 \\ i^{(m)} &= m \times [(1 + i)^{\frac{1}{m}} - 1] \end{aligned}

$d^{(m)}$ $d^{(m)}$ ：每一时期付 $m$ $m$ 次利息的名义贴现率
- 每 $1/m$ 个度量期支付利息一次，每 $1/m$ 个度量期上的实质贴现率为 $d^{(m)}/m$

\begin{aligned} 1 - d &= (1 - \frac{d^{(m)}}{m})^m \\ &\downarrow \\ d &= 1 - (1 - \frac{d^{(m)}}{m})^m \\ d^{(m)} &= m \times [1 - (1 -d)^{\frac{1}{m}}] \\ &= m \times (1 - v^{\frac{1}{m}}) \end{aligned}

利息强度

\delta_t = \frac{A'(t)}{A(t)} = \frac{a'(t)}{a(t)}

该投资在 $t$ 时的利息强度，利息最基本的度量就是利息强度。但在实务中，实质、名义利率与贴现率用得更多，因为它们更简单、更易理解，而且大多数金融业务涉及的是离散过程而非连续过程。这并不是说利息强度没有实际意义，除了它的理论意义外，实务中在计息非常频繁(如日计)的业务中，常用它来作近似计算。另外，近年来，有些金融业务已经开始使用连续复利了

价值等式

不同时刻支付的金额是不能直接进行比较的，金钱有时间价值，否则利率将无意义

time can do so much

四个基本量

原始投资的本金： $P$
投资时期的长度： $t$
利率： $i$
本金在投资期末的积累值： $A(t)$

年金

所谓年金是指一系列按照相等时间间隔支付的款项。

基本年金：利率为常数、计息频率与付款频率一致且每次付款为 1 的年金
- 系数为 C 的基本年金：对于其他条件相同，每次等额付款，但是付款额为 C 的（C≠1）年金

期末付年金

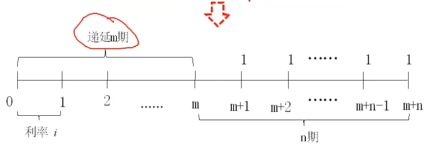
$a_n\rceil_i$ $a_{n} ⌉_{i}$ 在每个付款期末付款的基本年金为期末付年金。
- n期延付年金的现值。
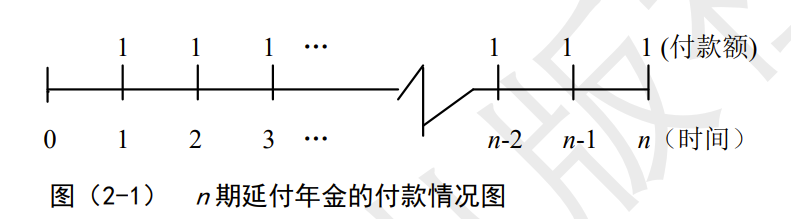
$s_n\rceil_i$ n期延付年金的终值。

n期标准期末年金：若年金的支付期限是n期，在每个期末支付年金额为1个货币单位

\begin{aligned} \text{0时刻一个单位货币} &= \text{每次利息收入i的现金流价值} + \text{n时刻一个单位货币的现值} \\ 1 &= i \times a_n\rceil_i + v^n \\ &\downarrow \\ a_n\rceil_i &= \frac{1 - v^n}{i} = \frac{\text{投资本金} - \text{投资本金的现值}}{\text{利率}} \\ &= \sum^n_{t=1} v^t \\ &\downarrow \\ \frac{a_n\rceil_i}{v^n} &= \frac{1 - v^n}{i \times v^n} \\ s_n\rceil_i &= \frac{(1 + i)^n - 1}{i} \end{aligned}

等比数列求和： $S_n = \frac{a_1(1 - q^n)}{1 - q}$

例子：已知半年换算名义利率为 $6$ %，某一10年期年金，每半年付款200元，计算该年金的现值

该年金半年实际利率为3%，10年内共付款20次

200 a_{20}\rceil_{3\%} = 200 * \frac{1 - 1.03^{-20}}{3\%} = 2975.49

终值为

200 s_{20}\rceil_{3\%} = 200 * \frac{(1 + 0.03)^{20} - 1}{3\%} = 5374.07

把一个现金流换算为了现在的价格，或者未来的价格
$a_{n}\rceil$ 是 n 项 1 的现值

假设有一笔总量为1的债务，如果用分别在接下来的 $n$ 期期末支付的 $n$ 次
等额还款来偿还的话，则每次还款量应该为

\frac{1}{a_{n}\rceil}

常数利率 $i$ 下，如果通过在今后 $n$ 期期末等额存款在n时积累到1。
每次需要存款量为

\frac{1}{s_{n}\rceil}

其中他们关系为

\frac{1}{a_{n}\rceil} = \frac{1}{s_{n}\rceil} + i

一笔金额为1，期限为 $n$ 的债务可以通过 $n$ 次等额支付来偿还，每次需还款 $\frac{1}{a_{n}\rceil}$
这笔债务也可以这样来还，在每期期末偿还利息 $i$ ，本金由一项等额的存款计划来积累，显然，存款计划的目标是在 $n$ 期期末积累到 1，而要实现这一目标则要求每次存款 $\frac{1}{s_{n}\rceil}$

例：实质利率为8%下，10年后攒够100000元，则每年末需要存多少

D = 100000 \times \frac{1}{s_{10}\rceil_{0.08}} = 6902.29

例：实质利率为7%下，存入10000元，4年取完，则每年末需要取多少

R = 10000 \times \frac{1}{a_{4}\rceil_{0.07}} = 2952.28

期初付年金

$\ddot{a}_n\rceil_i$ $\overset{a}{¨}_{n} ⌉_{i}$ 在每个付款期末付款的基本年金为期末付年金。
- n期延付年金的现值。
$\ddot{s}_n\rceil_i$ n期延付年金的终值。

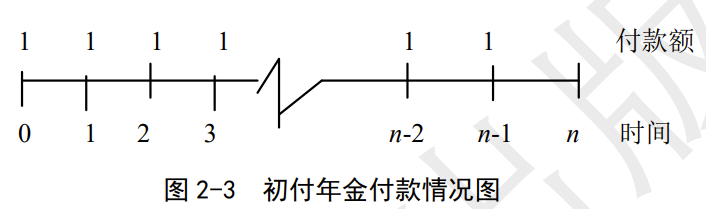
n期标准期初年金：若年金的支付期限是n期，在每个期初支付年金额为1个货币单位

\begin{aligned} \text{0时刻一个单位货币} &= \text{每次利息收入i的现金流价值} + \text{n时刻一个单位货币的现值} \\ 1 &= d \times \ddot{a}_n\rceil_i + v^n \\ &\downarrow \\ \ddot{a}_n\rceil_i &= \frac{1 - v^n}{d} = \frac{\text{投资本金} - \text{投资本金的现值}}{\text{贴现率}} \\ &= \sum^{n-1}_{t=0} v^t \\ &\downarrow \\ \frac{\ddot{a}_n\rceil_i}{v^n} &= \frac{1 - v^n}{d \times v^n} \\ \ddot{s}_n\rceil_i &= \frac{(1 + i)^n - 1}{d} \end{aligned}

其中他们关系为

\frac{1}{\ddot{a}_{n}\rceil} = \frac{1}{\ddot{s}_{n}\rceil} + i

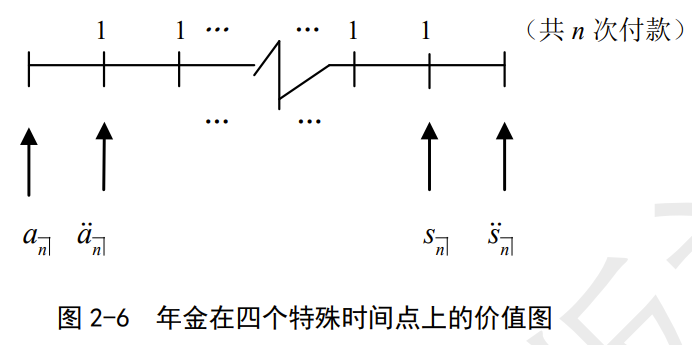
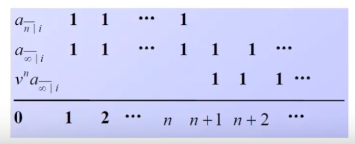
$a_{n}\rceil$ , $\ddot{a}_{n}\rceil$ , $s_{n}\rceil$ , $\ddot{s}_{n}\rceil$ 其实是同一项年金在不同时刻的价值。

\begin{aligned} \ddot{a}_{n}\rceil &= a_{n}\rceil(1+i) \\ \ddot{s}_{n}\rceil &= s_{n}\rceil(1+i) \end{aligned}

常见问题

第一次付款时刻多期前的年金值
最后一次付款时刻多期后的年金值

非整数问题

谓非标准期年金，指的是期数不为整数的年金，用符号表示即为

a_{n+k}\rceil

其中 $n$ 为整数， $0<k<1$

\begin{aligned} a_{n+k}\rceil &= \frac{1 - v^{n+k}}{i} \\ &= \frac{1 - v^n + v^n - v^{n+k}}{i} \\ &= a_{n}\rceil + v^{n+k}[\frac{(1+i)^k - 1}{i}] \end{aligned}

后一部分则可以看成是在 $n+k$ 时刻支付的 $s_k=\frac{(1+i)^k - i}{i}$ 在0时的现值， $v^{n+k}$ 为 $n+k$ 期贴现因子

0时的一笔大小为 $a_{n+k}\rceil$ 的债务，可以通过 $1, 2, \cdots, n$ 时分别还款为1，然后在 $n+k$ 时还款 $\frac{(1+i)^k - 1}{i}$ 来还清

其他年金

递延年金：年金的首次发生是递延了一段时间后进行的

永久年金：没有结束日期的年金

年金利率未知
变利率年金

假设 $n$ 期年金的各付款期上的利率分别为 $i_1, i_2, \cdots, i_n$ ，如果利率依时期而变，则所有付款的年金现值为

\begin{aligned} a_{n}\rceil &= (1 + i_i)^{-1} + (1+i_1)^{-1}(1+i_2)^{-1} + \cdots + (1+i_1)^{-1}(1+i_2)^{-1}\cdots (1+i_n)^{-1} \\ &= \sum^n_{t=1}\prod^t_{s=1}(1+i_s)^{-1} \\ s_{n}\rceil &= 1 + (1 + i_n) + (1+i_n)(1+i_{n-1}) + \cdots + (1+i_n)(1+i_{n-1})\cdots (1+i_2) \\ &= \sum^n_{t=1}\prod^{t-1}_{s=0}(1+i_{n-s+1}) \end{aligned} b

广义年金

付款时期间隔相同
每次付款额度相同
付款周期与计息周期不相同

例：每年末存入10000元，一共10年，月度转化利率为6%，求10年末积累值

i=(1+6\%/12)^{12}-1 = 6.17\% \\ 10000 s_{10}\rceil_i = 132864.99

例：贷款100000元，期限10年，每月末还款一次，每次还款额相等，贷款实质利率10%，求每次还款额

(1 + j)^{12} = 1 + 10\% \\ \downarrow \\ j = (1.1)^{1/12} - 1 = 0.7974\% \\ \downarrow \\ R=100000\times \frac{1}{a_{120}\rceil_j} = 1297.75

如果为月初还款

S=100000\times \frac{1}{\ddot{a}_{120}\rceil_j} = 1287.49

通过不同期限利率等价换算，使等价后的利率对应利息换算周期与付款周期一致，这样广义年金的相关计算就变为基本年金的相关计算

例：30w贷款，计划在未来5年内分季度在每季度末等量偿还，计算

贷款利率为半年换算名义利率10%

(1 + 10\%/2)^{2} = (1 + j\%)^2

贷款利率为月换算名义利率12%

(1 + 12\%/12)^{3} = (1 + j\%)

贷款利率为年实利率10%

(1 + 10\%) = (1 + j\%)^4

R a_{5\times 4}\rceil_j = 300000

实际运用

利息用于等于剩余本金 $\times$ 贷款利率，已还本金不会再产生利息

先息后本

先还利息，再还本金。
前面只还利息，最后一期还本金

等额本金

每个月还的本金等额，利息由剩余本金产生

等额本息

每个月还款的本金和利息是固定的

等本等息（分期手续费）

没有实质的等本等息

随借随换

随时借，随时还，一般按日息计算

年金5要素

PV现值： $PMT\times a_{n}\rceil_i$
FV终值： $PMT \times s_{n}\rceil_i$
PMT年金额
期数： $n$
利率： $i$

知道年金额，期数，利率

\text{现值} = PMT \times a_n\rceil_i = PMT \times \frac{1-(1+i)^{-n}}{i}

\text{终值} = PMT \times s_n\rceil_i = PMT \times \frac{(1+i)^n - 1}{i}

知道终值，期数，利率

PMT = FV \times \frac{1}{s_{n}\rceil_i}

知道现值，期数，利率

PMT = PV \times \frac{1}{a_{n}\rceil_i}

2段变动利率，求终值

FV = PMT \times s_n\rceil_{i_1}(1 + i_2)^{m} + PMT \times s_m\rceil_{i_2}

m度转化存款利率为 $i^{(m)}$ ，知道PMT和期数

i = (1 + \frac{i^{(m)}}{m})^{m} - 1 \\ FV = PMT \times s_m\rceil_{i}

知道实际利率，现值，期数，求每次还款额(分m次)

(1 + j)^{m} = 1 + i \\ \downarrow \\ j = (1 + i)^{\frac{1}{m}} - 1 \\ PMT = PV \times \frac{1}{a_n\rceil_j}

例子

贷款10000元，期限为10年，年实际利率为6%，计算

贷款本金和利息积累值在10年末一次性还清（一次还款）

10000 \times 1.06^{10} = 17908.48

每年末支付贷款利息，10年末归还本金（先息后本）

10000*0.06*10 + 10000 = 16000

利用基本年金的方式，每年末支付相同的金额，到10年末正好全部还清（等额本息）

\begin{aligned} R &= 10000*\frac{1}{a_{10}\rceil_{0.06}} \\ &= 10000*(\frac{1}{s_{10}\rceil_{0.06}} + 0.06) \\ &= 10000*(0.075868+0.06) \\ &=1358.68 \\ &\downarrow \\ 1368.68 &* 10 = 13586.80 \end{aligned}

等额本金

\sum_0^9 [(10000-1000n)*i + 1000] = 13300

FV为什么不是PMT乘期数

这是一个常见的误解。实际上，FV（终值）并不等于 PMT 乘以期数，这是因为还款中的每期金额不仅包含本金，还包括了利息，且利息随着时间的推移按复利计算。

详细解释：

PMT（每期还款金额） 是在考虑了贷款利率的情况下，每期还款的总金额。它包含了每期偿还的一部分本金以及当期应支付的利息。
如果直接将 PMT 乘以期数，那么我们仅仅计算了还款总额，即没有考虑利息的本金偿还额。但贷款期间你支付的利息是随着时间复利积累的，因此总还款的终值远高于简单的 PMT × 期数。

终值公式：

终值 $FV$ 计算的是一系列相同的现金流（即 PMT）在每期按一定利率增长后的累计金额，公式为：

FV = PMT \times \frac{(1 + r)^n - 1}{r}

其中：

$PMT$ 是每期的支付金额。
$r$ 是每期的利率（年利率除以12）。
$n$ 是期数。

由于每期支付的金额在未来都在产生利息，所以它们的终值会远大于 PMT 乘以期数。

举例：

利率 3% 的情况：
- PMT = 28,390.53 日元
- 如果简单地用 PMT × 60 期，则还款总额为 $28,390.53 × 60 = 1,703,431.80$ 日元。
- 但实际的终值为 1,835,354.51 日元，因为每期支付的金额在复利下累积产生了更多的利息。
利率 5% 的情况：
- PMT = 29,816.55 日元
- 简单计算为 $29,816.55 × 60 = 1,788,993.00 $ 日元。
- 实际终值为 2,027,706.71 日元，考虑了复利增长后的利息。

因此，终值是按复利计算的未来还款总额，而不仅仅是每期还款金额乘以期数。

差额是我之前付的钱产生的利息，我损失了这部分利息，但是一般生活里面实际付款都是PMT*乘期数

# 设定贷款金额和期数
loan_amount = 1580000  # 158万
periods = 60  # 60期

# 定义函数来计算PMT和FV
def calculate_pmt_fv(loan_amount, rate, periods):
    monthly_rate = rate / 12  # 月利率
    # 使用公式计算PMT：贷款本金 * (月利率 * (1 + 月利率)^期数) / ((1 + 月利率)^期数 - 1)
    pmt = loan_amount * (monthly_rate * (1 + monthly_rate) ** periods) / ((1 + monthly_rate) ** periods - 1)
    # 计算FV（终值）：PMT * ((1 + 月利率)^期数 - 1) / 月利率
    fv = pmt * ((1 + monthly_rate) ** periods - 1) / monthly_rate
    return pmt, fv

# 分别计算利率3%和5%的情况
pmt_3, fv_3 = calculate_pmt_fv(loan_amount, 0.03, periods)
pmt_5, fv_5 = calculate_pmt_fv(loan_amount, 0.05, periods)

参考

利息理论
《利息理论》南开大学出版社