[学习笔记] - 信号与系统入门

信号

信号：是传递，表达信息的物质载体。信号的基本形式是一些随着时间，空间或者其他变量发送变化物理量

• 电容充放
  • 自变量：时间
  • 因变量：电压，电流
• 声音信号
  • 自变量：时间
  • 因变量：声压
• 图像信号
  • 自变量：空间xy
  • 因变量：RGB亮度

信号分类

• 确定性信号与随机信号
  • 确定信号：是否能表示为函数
  • 随机信号
  • 伪随机信号：梅森旋转算法
  • 混沌信号
• 连续与离散信号
  • 连续时间信号
  • 离散时间信号
• 能量与功率信号
• 周期与非周期信号
  • 周期信号：满足$f(t + T) = f(t)$

---

• 数字信号
  • 时间离散，幅度离散
  • 例子：硬盘储存数据
• 模拟信号
  • 时间连续，幅度连续
  • 例子：声音，图像，气味，速度，体温，无线电
• 抽样信号
  • 时间离散，幅度连续
  • 例子：
• DA转换信号
  • 时间连续，幅度离散
  • 例子：得分情况

            graph TD
            模拟信号---信号采样-->抽样信号
抽样信号---数值量化-->数字信号
数字信号---零阶保持-->DA转换信号
DA转换信号---低通滤波-->模拟信号
          

---

连续时间信号
能量：

$E = \int^{\infty}_{-\infty}|f(t)|^2\mathrm{d}t$

离散时间信号
能量：

$E = \sum^{\infty}_{n=-\infty}|x[n]|^2$

范数

能量信号：能量有限信号$0 < E <+\infty$

连续时间信号
功率：一个周期的做工

$P = \lim_{T\rightarrow \infty}\frac{1}{T}\int^{T/2}_{-T/2}|f(t)|^2\mathrm{d}t$

离散时间信号
功率：

$P = \lim_{N \rightarrow \infty}\frac{1}{2N+1}\sum^N_{n=-N}|x[n]|^2$

功率信号：功率有限信号$0 < E <+\infty$

---

• 周期信号$T_1$ + 周期信号$T_2$ = 周期信号$T_3 \rightarrow$ 傅里叶级数分解
  • $T_1, T_2$存在最小公倍数$T_3$
• 周期信号$T_1$ + 周期信号$T_2$ = 非周期信号$\rightarrow$ 傅里叶变换
  • $T_1, T_2$不存在最小公倍数$T_3$
• 周期信号$T_1$ + 非周期信号 = 非周期信号
• 周期信号$T_1$ + 非周期信号 = 周期信号$T_2$

系统

系统：是由若干相互作用和相互依赖的事务组合而成的具有特定功能的整体

            graph LR
            输入-->系统
系统-->输出
          

• 连续时间系统
• 离散时间系统

线性时不变系统

描述信号

连续时间信号

数学描述方式

$\begin{aligned} f(t) &= k\sin(\omega t + \theta) & \\ f(t) &= e^{at} & \text{指数信号} \\ f(t) &= ke^{(a+iw)t} & \text{复指数信号} \end{aligned}$

离散时间信号

指数序列

$f[n] = ke^{-0.15n}, n =1, 2, \cdots, n$

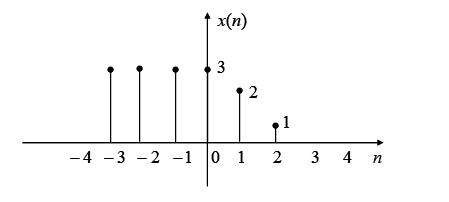
正弦震荡序列

$x[n] = 3\cos[\frac{4\pi n}{25}], n =1, 2, \cdots, n$

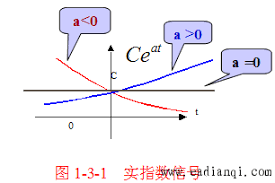
指数信号

$f(t) = ke^{at} \quad a,k \in \mathbb{R}$

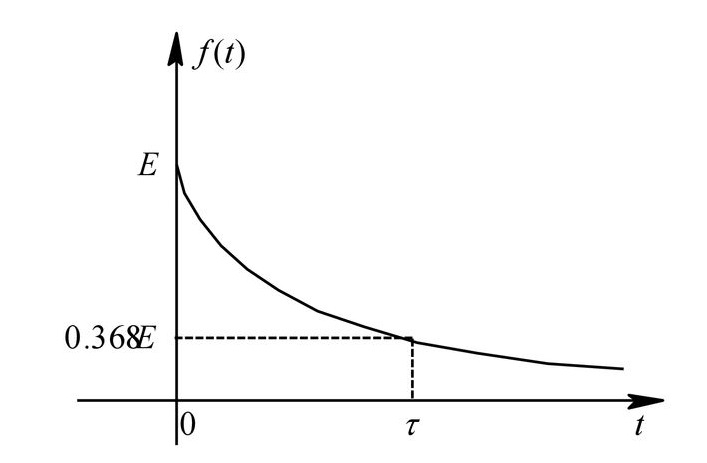
单边指数信号

$f(t) = \begin{cases} ke^{at} & t \geq 0 \\ 0 & t < 0 \end{cases}$

经过$\tau$时间，信号衰减到$\frac{k}{e}$，经过$2\tau$时间，信号衰减到$\frac{k}{e^2}$，

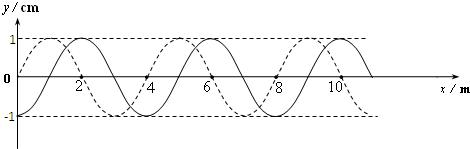
正弦信号

$f(t) = k\sin(\omega t + \theta)$

单边指数衰减正弦信号

$\text{正弦信号} \times \text{单边指数信号}$

$f(t) = \begin{cases} ke^{at}\sin(\omega t + \theta) & t \geq 0 \\ 0 & 0 \end{cases}$

• 幅度：$k$
• 增长趋势：$a$
• 震荡频率：$\omega$
• 相位：$\theta$

记$s = a + i\omega$，$k = |k|e^{i\theta}$，则可表示为$ke^{st}$

$\begin{aligned} f(t) &= ke^{st} \begin{cases} s &= \sigma + j\omega \\ k &= x + jy = |k|e^{i\theta} \quad \theta = tg^{-1}\frac{y}{x} \end{cases} \\ &= |k|e^{i\theta}e^{(a+i\omega)t} \\ &= |k|e^{at + i(\omega t + \theta)} \\ &= |k|e^{at}e^{i(\omega t + \theta)} \\ &= |k|e^{at}\cos(\omega t + \theta) + i|k|e^{at}\sin(\omega t + \theta) \end{aligned}$

直流	指数	正弦	余弦	幅度变化震荡	幅度变化震荡
$\omega = 0$	$\omega = 0$	$\omega \neq 0$	$\omega \neq 0$	$\omega \neq 0$	$\omega \neq 0$
$\sigma = 0$	$\sigma \neq 0$	$\sigma = 0$	$\sigma = 0$	$\sigma > 0$	$\sigma < 0$
		实部	虚部	增长震动	衰弱震荡

LTI系统的特征信号：微分积分函数形式不改变

高斯信号

$f(t) = Ee^{-(\frac{t}{\sigma})^2}$

• $E$：信号初始值高度
• $\sigma$：信号的宽度

抽样信号

$sinc = f(t) = Sa(t) = \frac{\sin(t)}{t} = \begin{cases} 1 & t = 0 \\ \frac{\sin t}{t} & t \neq 0 \end{cases}$

整体呈现$1/t$的衰减趋势
积分面积

$\int^{\infty}_{-\infty} Sa(t)\mathrm{d}t = \pi$

傅里叶变换：$Sa(t) \leftrightarrow G(\omega)$

奇异信号

函数本身或者其导数存在不连续点的信号

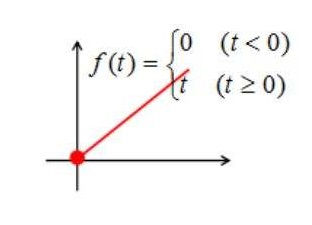
单位斜变信号

$f(t) = \begin{cases} t & t \geq 0 \\ 0 & t < 0 \end{cases}$

单位阶跃信号

$u(t) = \begin{cases} 1 & t > 0 \\ 1/2 & t = 0 \\ 0 & t < 0 \end{cases}$

可以使用$u(t)$来截取信号的大于$0$的部分

$f(t)u(t - t_0)$

表示截取信号从$t_0$开始往后的部分

窗口信号

$u(t) - u(t - t_0)$

$u(t + \frac{\tau}{2}) - u(t - \frac{\tau}{2})$

分段信号

可以通过$u(t)$构建分段信号

截取信号

截取信号有限长度部分

定义符号函数

$sgn(t) = \begin{cases} 1 & t > 0 \\ -1 & t < 0 \end{cases} = 2u(t) - 1$

单位冲激信号

$\delta(t) = \begin{cases} +\infty & t = 0 \\ 0 & t \neq 0 \end{cases}$

$\int^{+\infty}_{-\infty}\delta(t)dt = 1$

抽样特性

$\int^{\infty}_{-\infty}\delta(t)f(t)\mathrm{d}t = \int^{0_+}_{0_-}\delta(t)f(0)\mathrm{d}t = f(0)$

$\int^{\infty}_{-\infty}\delta(t - t_0)f(t)\mathrm{d}t = f(t_0)$

单位冲击偶信号

$\delta'(t) = \frac{\mathrm{d}\delta(t)}{\mathrm{d}t}$

	$\delta(t)$	$\delta'(t)$
奇偶对称	$\delta(-t) = \delta(t)$	$\delta'(-t) = -\delta'(t)$
抽样	$f(t)\delta(t) = f(0)\delta(t)$	$f(t)\delta'(t)=f(0)\delta'(t)-f'(0)\delta(t)$
抽样	$\int^{\infty}_{-\infty}f(t)\delta(t)\mathrm{d}t = f(0)$	$\int^{\infty}_{-\infty}f(t)\delta'(t)\mathrm{d}t = -f'(0)$
积分	$\int^t_{-\infty}\delta(\tau)\mathrm{d}\tau = u(t)$	$\int^t_{-\infty}\delta'(\tau)\mathrm{d}\tau = \delta(t)$
卷积	$f(t)*\delta(t)=f(t)$	$f(t)*\delta'(t) = \frac{\mathrm{d}}{\mathrm{d}t}f(t)$

信号的运算

幅值：$kf(t)$
移动：$f(t - t_0)$
拉伸压缩：$f(at)$
反褶：$f(-t)$
微分：信号关于时间的变换率

$\frac{\mathrm{d}}{\mathrm{d}t}f(t)$

积分：信号作用量的累积效果

$\int^t_{-\infty}f(\tau)\mathrm{d}\tau$

相加：$f(t) + g(t)$
相乘：$f(t) \cdot g(t)$
卷积：$f(t)*g(t) = \int^{+\infty}_{\infty}f(\tau)\cdot g^*(t - \tau)\mathrm{d}\tau$
相关：$R_{f,g}(t) = \int^{+\infty}_{\infty}f(\tau)\cdot g^*(\tau - t)\mathrm{d}\tau$