[学习笔记] - 模式识别

为了能让机器执行和完成识别任务，必须对分类识别对象进行科学的抽象，建立它的数学模型，用以描述和代替识别对象，这种对象的描述即为模式。

特征矢量
符号串
图
关系式

            graph TD
            学习训练-->分类识别

模式识别的核心问题

            graph LR
            特征提取与选择-->训练学习
训练学习-->分类识别

统计模式识别
- 模糊模式识别
- 线性分类器
  - 感知器
  - LMSE算法
  - 支持向量机
- 贝叶斯分类器
  - 最小错误率
  - 最小风险
  - 朴素贝叶斯
- 最近邻分类器
  - 模板匹配
  - K近邻算法
- 神经网络分类器
  - 多层感知器
  - BP网络
  - 深度学习
- 统计聚类算法
  - 层次聚类
  - 动态聚类
结构模式识别
- 结构聚类算法
- 句法模式识别

基本原则

没有免费午餐定理
丑小鸭定理
最小描述定理

绪论

特征矢量

一个分析对象的 $n$ 个特征量测值分别为 $x_1, x_2, \cdots, x_n$ ，它们构成一个 $n$ 维特征矢量 $\mathbf{x}$

\mathbf{x} = (x_1, x_2, \cdots, x_n)

$\mathbf{x}$ 是原对象（样本）的一种数学抽象，用来表示原对象，即为原对象的模式

特征空间

对某对象的分类识别是对其模式，即它的特征矢量进行分类识别。

各种不同取值的 $\mathbf{x}$ 的全体构成了 $n$ 维空间，这个 $n$ 维空间称为特征空间，不同的场合的特征空间可以记为 $X^n$ ， $R^n$ 。特征矢量 $\mathbf{x}$ 便是特征空间中的一个点，所以也称特征点

随机变量

由于测量系统随机因素的影响及不同对象的特征本身就是在特征空间散布的，同一个对象或同一类对象的某特征量测值是随机变量，由随机分量构成的矢量称为随机矢量，同一类对象的特征矢量在特征空间中是按照某种统计规律随机散布的

随机矢量的分布函数

设

随机矢量： $\mathbf{X} = (X_1, X_2, \cdots, X_n)^T$
确定型矢量： $\mathbf{x} = (x_1, x_2, \cdots, x_n)^T$

随机矢量 $\mathbf{X}$ 的联合概率分布函数定义为

F(x_1, x_2, \cdots, x_n) = P(X_1 \leq x_1, X_2 \leq x_2, \cdots, X_n \leq x_n)

写成矢量形式

F(\mathbf{x}) = P(\mathbf{X} < \mathbf{x})

联合概率密度函数

设

随机矢量： $\mathbf{X} = (X_1, X_2, \cdots, X_n)^T$
确定型矢量： $\mathbf{x} = (x_1, x_2, \cdots, x_n)^T$

随机矢量 $\mathbf{X}$ 的联合概率密度函数定义为

p(x_1, x_2, \cdots, x_n) = \frac{\partial^nF(x_1, x_2, \cdots, x_n)}{\partial x_1, \partial x_2, \cdots, \partial x_n}

类概率密度函数

设集合由 $c$ 类模式组成，第 $i$ 类记为 $\omega_i$ ， $\omega$ 类模式特征矢量有自己的分布函数和密度函数

\begin{aligned} F(\mathbf{x}|\omega_i) &= P(\mathbf{X} \leq \mathbf{x}|\omega_i) \\ p(\mathbf{x}|\omega_i) &= \frac{\partial^nF(x_1, x_2, \cdots, x_n|\omega_i)}{\partial x_1, \partial x_2, \cdots, \partial x_n} \end{aligned}

随机矢量的数学特征

随机矢量数学期望

$n$ 维随机矢量 $\mathbf{X}$ 的数学期望 $\mu$ 定义为

\mathbf{\mu} = E[\mathbf{X}] = \overline{\mathbf{X}} = \begin{bmatrix} E[X_1] \\ E[X_2] \\ \cdots \\ E[X_n] \end{bmatrix} = \int_{X^n} \mathbf{x}p(\mathbf{x})\mathrm{d}x

随机矢量条件期望

在模式识别中，经常以类别 $\omega_i$ 作为条件，在这种情况下随机矢量 $\mathbf{X}$ 的条件期望矢量定义为

\mathbf{\mu_i} = E[\mathbf{X}|\omega_i] = \int_{X^n} \mathbf{x}p(\mathbf{x}|\omega_i)\mathrm{d}x

协方差矩阵

给定 $n$ 元的多维随机变量 $\mathbf{X}$ 和 $m$ 元的多维随机变量 $\mathbf{Y}$ ，则它们的协方差矩阵为

\begin{aligned} Cov(\mathbf{X}, \mathbf{Y}) = \Sigma &= \begin{bmatrix} Cov(x_1,y_1) & Cov(x_1,y_2) & \cdots & Cov(x_1,y_m) \\ Cov(x_2,y_1) & Cov(x_2,y_2) & \cdots & Cov(x_2,y_m) \\ \vdots & \vdots & \ddots & \vdots \\ Cov(x_n,y_1) & Cov(x_n,y_2) & \cdots & Cov(x_n,y_m) \end{bmatrix} \\ &= E(\mathbf{X}\mathbf{Y}^T) - E(\mathbf{X})E(\mathbf{Y})^T \end{aligned}

其中 $Cov(\mathbf{X}, \mathbf{X})$ 为 $\mathbf{X}$ 自身的协方差矩阵可以写作

\begin{aligned} Cov(\mathbf{X}, \mathbf{X}) &= E((\mathbf{X} - \mathbf{\mu})(\mathbf{X} - \mathbf{\mu})^T) = E(\mathbf{X}\mathbf{X}^T) - \mathbf{\mu}\mathbf{\mu}^T \\ &= (\sigma_{ij}^2)_{n\times n} \end{aligned}

自相关矩阵

随机矢量 $\mathbf{X}$ 的自相关矩阵定义为

R = E[\mathbf{X}\mathbf{X}^T]

由定义可知， $\mathbf{X}$ 的协方差矩阵和自相关矩阵间的关系是

\Sigma = \mathbf{R} - \mathbf{X}\mathbf{X}^T = \mathbf{R} - \mu\mu^T

对称非负定矩阵

协方差矩阵和自相关矩阵都是对称矩阵，设 $A$ 为对称矩阵，对任意的矢量 $\mathbf{x}$ ，由二次型 $\mathbf{x}^TA\mathbf{x}$ ，若对任意的 $\mathbf{x}$ 恒有

\mathbf{x}^TA\mathbf{x} \geq 0

则称 $A$ 为非负定矩阵

协方差矩阵是非负定的

不相关

随机矢量 $\mathbf{X}$ 的第 $i$ 分量 $X_i$ ，和第 $j$ 个分量 $X_j$ ，若有 $\sigma^2_{ij} = 0(i \neq j)$ ，则称它们不相关

等价条件：

E[X_iX_j] = E[X_i]E[X_j]

随机矢量 $\mathbf{X}$ 和 $\mathbf{Y}$ 不相关的充要条件是互协方差矩阵 $Cov(X,Y) = \mathbf{0}$ ，即

E[\mathbf{X}\mathbf{Y}^T] = E[\mathbf{X}]E[\mathbf{Y}^T]

正交

若随机矢量 $\mathbf{X}$ 和 $\mathbf{Y}$ 满足

E[X^TY] = \mathbf{0}

则称 $\mathbf{X}$ 和 $\mathbf{Y}$ 正交

独立

若随机矢量 $\mathbf{X}$ 和 $\mathbf{Y}$ 的联合概率密度函数 $p(x, y)$ ，若满足 $p(x, y) = p(x)p(y)$ ，则称它们独立

独立必不相关，反之不一定

随机矢量的变换

设随机矢量 $\mathbf{Y}$ 是另一个随机矢量 $\mathbf{X}$ 的连续函数，即

\mathbf{Y} = \begin{bmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_n \end{bmatrix} = \begin{bmatrix} g_1(X_1, X_2, \cdots, X_n) \\ g_2(X_1, X_2, \cdots, X_n) \\ \vdots \\ g_n(X_1, X_2, \cdots, X_n) \end{bmatrix} = \begin{bmatrix} g_1(\mathbf{X}) \\ g_2(\mathbf{X}) \\ \vdots \\ g_n(\mathbf{X}) \end{bmatrix} = \mathbf{g}(\mathbf{X})

若它们的函数关系是一一对应的，则两个随机矢量的概率密度函数之间有关系

\begin{aligned} p(\mathbf{y}) &= \frac{p(\mathbf{x})}{J} \\ J &= \begin{vmatrix} \frac{\partial g_1}{\partial x_1} & \frac{\partial g_1}{\partial x_2} & \cdots & \frac{\partial g_1}{\partial x_n} \\ \frac{\partial g_2}{\partial x_1} & \frac{\partial g_2}{\partial x_2} & \cdots & \frac{\partial g_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial g_n}{\partial x_1} & \frac{\partial g_n}{\partial x_2} & \cdots & \frac{\partial g_n}{\partial x_n} \end{vmatrix} \end{aligned}

$J$ 为雅可比行列式，表示变换后体积微元的变化， $Y^n$ 坐标系中体积微元

\mathrm{d}y_1\mathrm{d}y_2\cdots\mathrm{d}y_n = |J|\mathrm{d}x_1\mathrm{d}x_2\cdots\mathrm{d}x_n

\mathbf{Y} = \begin{bmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_n \end{bmatrix} = \begin{bmatrix} a_{11}X_1, a_{12}X_2, \cdots, a_{1n}X_n) \\ a_{21}X_1, a_{22}X_2, \cdots, a_{2n}X_n) \\ \vdots \\ a_{n1}X_1, a_{n2}X_2, \cdots, a_{nn}X_n) \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} \begin{bmatrix} \mathbf{X} \\ \mathbf{X} \\ \vdots \\ \mathbf{X} \end{bmatrix} = A\mathbf{X}

此时 $J = |A|$ ，则随机矢量 $\mathbf{Y}$ 的概率密度函数

p(\mathbf{y}) = \frac{p(\mathbf{x})}{||A||}

设 $\mathbf{X}$ 的均值矢量为 $\mathbf{\mu}_x$ ，协方差矩阵为 $\Sigma_x$ ，则

Y均值矢量： $\mathbf{\mu}_y = E[\mathbf{Y}] = AE[\mathbf{X}] = A\mathbf{\mu}_x$
Y协方差矩阵： $\Sigma_y = AE[(\mathbf{X} - \mathbf{\mu}_x)(\mathbf{X} - \mathbf{\mu}_x)^T]A^T = A\Sigma_xA^T$

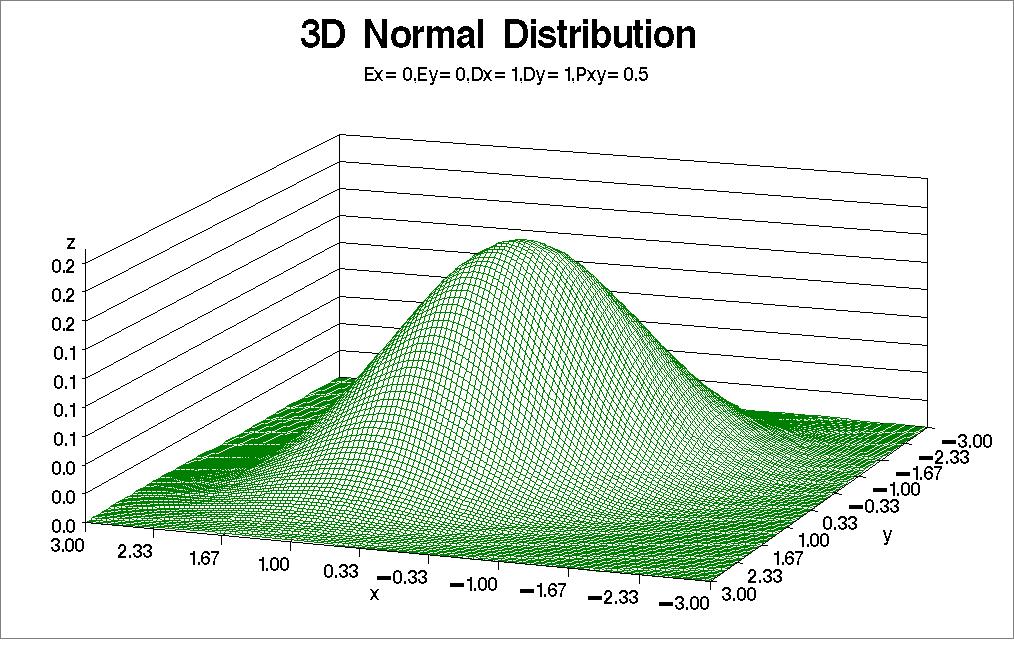
正态分布

许多随机变量近似服从正太分布
是许多重要概率分布的极限分布

p(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp[-\frac{(x - \mu)^2}{2\sigma^2}]

多变量正态分布

$n$ 元正态分布的随机矢量 $\mathbf{X} = (X_1, X_2, \cdots, X_n)^T$ 的概率密度函数定义为

\begin{aligned} p(x_1, x_2, \cdots, x_n) &= p(\mathbf{x}) \\ &= \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}\exp \left[-\frac{1}{2}(\mathbf{x} - \mathbf{\mu})^T\Sigma^{-1}(\mathbf{x} - \mathbf{\mu})\right] \end{aligned}

完全由 $\mathbf{x}$ 和 $\Sigma$ 确定： $\mathbf{X} \sim N(\mu, \Sigma)$
等概率密度点的轨迹为超椭球面
不相关与独立式等价的
多元正态随机矢量 $\mathbf{X}$ 的边缘概率密度的条件概率密度仍是正态分布
$\mathbf{X}$ 的线性变换仍为多元正态随机矢量
$\mathbf{X}$ 的分量的线性组合式一多元正态随机变量

聚类分析

假设：对象集客观存在着若干个自然类，每个自然类中个体的某些属性具有较强的相似性
原理：将给定的模式分成若干组，每组内的模式是相似的，而组内各模式差别较大
基本思想：

相似的归为一类
模型相似性的度量和聚类算法
无监督分类

聚类是无监督的

特征量的类型

物理量 - （重量，长度，速度）
次序量 - （等级，技能，学识）
名义量 - （性别，状态，种类）

方法的有效性：取决于分类算法和特征点分布情况的匹配

特征选取不当使分类无效
特征选取不足可能使不同类别判为一类
特征选取过多可能无益反而有害，增加负担，效果变差
量纲选取不当

聚类分析的基本思想

特征提取
模式相似度量
点与类间的距离
类与类间的距离
聚类准则及聚类算法
有效性分析

模式相似性测度

用于描述个模式之间特征的相似程度

距离测度

测度基础：两个矢量矢端的距离
测度数值：两矢量各相应分量之差的函数

设矢量 $\vec{x}$ 和 $\vec{y}$ 的距离为 $d(\vec{x}, \vec{y})$

$d(\vec{x}, \vec{y}) \geq 0$ ，当且仅当 $\vec{y} = \vec{x}$ 时，等号成立
$d(\vec{x}, \vec{y}) = d(\vec{y}, \vec{x})$
$d(\vec{x}, \vec{y}) \leq d(\vec{x}, \vec{z}) + d(\vec{z}, \vec{y})$

欧式距离

d(\vec{x}, \vec{y}) = ||\vec{x} - \vec{y}|| = \sqrt{\sum^n_{i=1} (x_i - y_i)^2}

绝对值距离

d(\vec{x}, \vec{y}) = \sum^n_{i=1}|x_i - y_i|

街坊距离

切氏距离

d(\vec{x}, \vec{y}) = \max_i|x_i - y_i|

明氏距离

d(\vec{x}, \vec{y}) = \left[ \sum^n_{i=1}|x_i - y_i|^m\right]^{\frac{1}{m}}

马氏距离

设 $n$ 维矢量 $\overline{x}_i$ 和 $\overline{x}_j$ 是矢量集 $\lbrace \overline{x}_1, \overline{x}_2, \cdots, \overline{x}_m \rbrace$ 中的两个矢量，马氏距离为

d^2(\vec{x}_i, \vec{x}_j) = (\vec{x}_i - \vec{x}_j)^TV^{-1}(\vec{x}_i - \vec{x}_j)

其中

\begin{aligned} V &= \frac{1}{m - 1}\sum^m_{i=1}(\vec{x}_1 - \overline{\vec{x}})^T(\vec{x}_i - \overline{\vec{x}}) \\ \overline{\vec{x}} &= \frac{1}{m}\sum^m_{i=1}\overline{x}_i \end{aligned}

与量纲无关，对一切非奇异线性变换都是不变的，具有坐标系比例，选择，平移不变性，从统计意义上尽量去掉了分量间的相关性

相似测度

测度基础：两个矢量的方向是否相近作为考虑的基础，矢量长度并不重要

角度相似系数

\cos(\vec{x}, \vec{y}) = \frac{\vec{x}\vec{y}}{||\vec{x}||\cdot||\vec{y}|||}

对坐标系的旋转和尺度的缩放具有不变性

指数相似系数

e(\vec{x}, \vec{y}) = \frac{1}{n}\sum^n_{i=1}\exp[-\frac{3}{4}\frac{(x_i - y_i)^2}{\sigma^2_i}]

$\sigma^2_i$ ：相应分量的协方差
$n$ ：矢量维数

匹配测度

当特征只有两个状态 $(0, 1)$ 时，常用匹配测度， $0$ 表示无此特征， $1$ 表示有此特征，故称之为二值特征，对于给定的 $\mathbf{x}$ 和 $\mathbf{y}$ 中的某两个相应的分量 $x_i$ 与 $y_j$

\begin{aligned} \mathbf{x} = 0,1,0,1,1,0 \\ \mathbf{y} = 0,0,1,1,0,1 \end{aligned}

若 $x_i = 1, y_i = 1$ ，则称 $x_i$ 与 $y_i$ 是 $(1-1)$ 匹配
若 $x_i = 1, y_i = 0$ ，则称 $x_i$ 与 $y_i$ 是 $(1-0)$ 匹配
若 $x_i = 0, y_i = 1$ ，则称 $x_i$ 与 $y_i$ 是 $(0-1)$ 匹配
若 $x_i = 0, y_i = 0$ ，则称 $x_i$ 与 $y_i$ 是 $(0-0)$ 匹配

对于二值 $n$ 维特征矢量可定义如下相似性测度

$a = \sum_{i}x_iy_i$ ：为 $\vec{x}, \vec{y}$ 的 $(1-1)$ 匹配的特征数目
$b = \sum_{i}y_i(1 - x_i)$ ：为 $\vec{x}, \vec{y}$ 的 $(0-1)$ 匹配的特征数目
$a = \sum_{i}x_i(1 - y_i)$ ：为 $\vec{x}, \vec{y}$ 的 $(1-0)$ 匹配的特征数目
$a = \sum_{i}(1 - x_i)(1 - y_i)$ ：为 $\vec{x}, \vec{y}$ 的 $(0-0)$ 匹配的特征数目

Tanimoto测度

s(\vec{x}, \vec{y}) = \frac{a}{a + b + c} = \frac{\vec{x}^T\vec{y}}{\vec{x}^T\vec{x} + \vec{y}^T\vec{y} - \vec{x}^T\vec{y}}

它等于共同具有的特征数目与分别具有的特征种类总数之比

Rao测度

s(\vec{x}, \vec{y}) = \frac{a}{a + b + c + e} = \frac{\vec{x}^T\vec{y}}{n}

为 $(1-1)$ 匹配特征数目和所选用的特征数目之比

简单匹配系数

(\vec{x}, \vec{y}) = \frac{a + e}{n}

上式分子为 $(1-1)$ 匹配特征数目与 $(0-0)$ 匹配特征数目之和，分母为所考虑的特征数目

Dice系数

m(\vec{x}, \vec{y}) = \frac{a}{2a + b + c} = \frac{\vec{x}^T\vec{y}}{\vec{x}^T\vec{x} + \vec{y}^T\vec{y}} = \frac{(1-1)\text{匹配个数}}{\text{两矢量中1的个数}}

Kulzinsky系数

m(\vec{x}, \vec{y}) = \frac{a}{b + c} = \frac{\vec{x}^T\vec{y}}{\vec{x}^T\vec{x} + \vec{y}^T\vec{y} - 2\vec{x}^T\vec{y}} = \frac{(1-1)\text{匹配个数}}{(0-1)+(1-0)\text{匹配个数}}

类的定义与类间距离

类的约束：对于一个待分类的集合 $S$ ，要求分类后的各类 $S_1, S_2, \cdots, S_c$ 满足

$S_i \neq \varnothing$
$\cup^c_{i=1}S_i = S$
$S_i \cup S_j = \varnothing, \quad i \neq j$

类的定义

定义：若集合 $S$ 中任两个元素 $x_i$ ， $x_j$ 的距离 $d_{ij}$ 有

d_{ij} \leq h

则称 $S$ 相对于阈值 $h$ 组成一类

此类中任意2元素之间距离小于 $h$

定义：若集合 $S$ 中任一元素 $x_i$ 与其他各元素 $x_j$ 间的距离 $d_{ij}$ 均满足

\frac{1}{k-1}\sum_{x_j \in S}d_{ij} \leq h

则称 $S$ 相对于阈值 $h$ 组成一类（ $k$ 为集合元素个数）

定义：若集合 $S$ 中任一元素 $x_i$ 与其他各元素 $x_j$ 间的距离 $d_{ij}$ 均满足

\frac{1}{k(k-1)}\sum_{x_i\in S}\sum_{x_j\in S}d_{ij} \leq h ,\quad d_{ij} \leq r

则称 $S$ 相对于阈值 $h,r$ 组成一类

定义：若集合 $S$ 中任一元素 $x_i$ ，都存在某元素 $x_j\in S$ 使它们的距离 $d_{ij}$ 满足

d_{ij} \leq h

则称 $S$ 相对于阈值 $h$ 组成一类

类的距离定义

最远距离法

D_{kl} = \max_{i,j}\lfloor d_{ij} \rfloor

中心距离法

D^2_{kl} = \frac{1}{2}D_{kp}^2 + \frac{1}{2}D_{kp}^2 - \frac{1}{4}D^2_{pq}

没有考虑样本数量

重心距离法

中心距离法考虑样本数量之后（权重）

D^2_{kl} = \frac{n_p}{n_p+n_q}D_{kp}^2 + \frac{n_q}{n_p+n_q}D_{kp}^2 - \frac{n_pn_q}{(n_p+n_q)^2}D^2_{pq}

平均距离法

D_{pq}^2 = \frac{1}{n_pn_q} \sum d^2_{ij}

所有点的距离的平均

离差平方和距离法

\begin{aligned} D^2_{kl} &= \frac{n_k + n_p}{n_k + n_l}D^2_{kp} + \frac{n_k + n_q}{n_k + n_l}D^2_{kq} - \frac{n_k}{n_k + n_l}D^2_{pq} \\ \\ s_t &= \sum_{\mathbf{x}_i \in \omega}(\mathbf{x}_i - \mathbf{x}_t)^T(\mathbf{x}_i - \mathbf{x}_t) \\ D^2_{pq} &= s_l - s_p - s_q \\ &= \frac{n_pn_q}{n_p+n_q}(\mathbf{x}_p - \mathbf{x}_q)^T(\mathbf{x}_p - \mathbf{x}_q) \end{aligned}

$\mathbf{x}_p,\mathbf{x}_q,\mathbf{x}_t$ 分布为对应类的重心

准则函数

点和集合的距离

第一类：对集合的分布没有先验知识时，可采用类间距离计算
第二类：当知道集合的中点分布的先验知识时，可用相应的模型进行计算

聚类的准则函数

标准：内间距离小，类间距离大
设有待分类的模式集 $\lbrace \mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n \rbrace$ 在某种相似性测度基础上被划分为 $c$ 类，类内距离准则函数 $j_w$ 定义为

j_w = \sum^c_{j=i}\sum^{n_j}_{i=1}(\mathbf{x}_i^{(j)} - \mathbf{m}_j)^2 \quad \mathbf{m}_j \text{表示} \omega_j \text{类的模式均值矢量}

加权聚类的准则函数

j_{ww} = \sum^c_{j=1}\frac{n_j}{N}\overline{d}_j^2 \qquad \overline{d}_j^2 = \frac{2}{n_j(n_j - 2)}\sum||\mathbf{x}^{(j)}_j - \mathbf{x}_k^{(j)}||

$\sum||\mathbf{x}^{(j)}_i - \mathbf{x}_k^{(j)}||$ ：表示 $\omega_j$ 类内任意两个模式距离平方和
$\overline{d}_j^2$ ：表示类内两模式间的均方距离
$N$ ：待分类模式总数
$\frac{n_j}{N}$ ：表示 $\omega_j$ 类先验概率的估计-频率

类间距离准则函数

J_B = \max\sum^c_{j=1}(\mathbf{m}_j - \mathbf{m})^T(\mathbf{m}_j - \mathbf{m})

$\mathbf{m}_j$ ：为 $\omega_j$ 类的模式平均矢量
$\mathbf{m}$ ：为总的模式平均矢量

加权类间距离准则函数

J_{WB} = \max\sum^c_{j=1}\frac{n_j}{N}(\mathbf{m}_j - \mathbf{m})^T(\mathbf{m}_j - \mathbf{m})

对于两类问题，类间距离有时取

J_{B2} = (\mathbf{m}_1 - \mathbf{m}_2)^T(\mathbf{m}_1 - \mathbf{m}_2)

$J_{B2}$ 和 $J_{WB}$ 的关系是： $J_{WB} = \frac{n_1}{N}\frac{n_2}{N}J_{B2}$

聚类的准则函数+类间距离准则函数

我们希望内间距离小，类间距离大，所以构造出能够同时反映出它们的类间距离的准则函数最好
设待分类 $\lbrace \mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n \rbrace$ ，分为 $c$ 类，每个类含 $n_j$ 和模式 $\mathbf{x}^{(j)}_i$

$\omega_j$ 的类内离差阵（样本协方差矩阵但是没有减1）定义为

S^{(j)}_w = \frac{1}{n_j}\sum^{n_j}_{i=1}(\mathbf{x}^{(j)}_i - \mathbf{m}_j)(\mathbf{x}^{(j)}_i - \mathbf{m}_j)^T \quad j = 1, 2, \cdots, c

见[学习笔记] - 多元统计分析 #极大似然估计多元正态分布

$\mathbf{m}_j$ ：为 $\omega_j$ 类的模式平均矢量
总的类内离差阵： $S_w = \sum^c_{j=1}\frac{n_j}{N}S^{(j)}_w$
类间离差阵： $S_B = \sum^c_{j=1}\frac{n_j}{N}(\mathbf{m}_j - \mathbf{m})(\mathbf{m}_j - \mathbf{m})^T$
总的离差阵： $S_r = \frac{1}{N}\sum^N_{i=1}\frac{n_j}{N}(\mathbf{m}_i - \mathbf{m})(\mathbf{m}_i - \mathbf{m})^T$

S_r = S_w + S_B

聚类的基本目的是 $\max tr(S_B)$ 或 $\min tr(S_w)$ ，利用线性代数有关矩阵的迹和行列式的性质，可以定义如下4个聚类的准则函数

\begin{aligned} J_1 &= tr(S^{-1}_wS_B) \\ J_2 &= |S^{-1}_wS_B| \\ J_3 &= tr(S^{-1}_wS_T) \\ J_4 &= |S^{-1}_wS_T| \end{aligned}

为了得到更好的聚类结果，应该使它们尽量的大

聚类的算法

按最小距离原则简单聚类方法
按最小距离原则进行两类合并的方法
依据准则函数动态聚类方法

简单聚类方法

确定一个相似性阈值，将模式到各聚类中心间的距离与阈值比较

当大于阈值就作为另一类的类心
当小于阈值就按最小距离原则将其划分到某一类中

模式的类别及类的中心一旦确定将不会改变，聚类结果很大程度依赖 $T$ 的选取，初始值的选取，和选模式的顺序也会造成不同

设待分类 $\lbrace \mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n \rbrace$ ，选定类间距离阈值 $T$
计算模式特征矢量到聚类中心的距离并合并门限 $T$ 比较，决定归属该类或作为新的一类中心，通常选择欧式距离

任取一个模式特征矢量作为第一个聚类中心 $\mathbf{z}_1$
计算下一个模式特征矢量计算 $\mathbf{x}_2$ $x_{2}$ 到 $\mathbf{z}_1$ $z_{1}$ 的距离
1. 若大于 $T$ ，则新建一类并作为中心
2. 若小于 $T$ ，则属于这一类
对于尚未确定类别的模式，计算到各聚类中心的聚类进行判断

最小距离两类合并

首先全部作为一类，然后将距离最小的两类合并为一类，不断重复，直到分为2类位置
类心不断修正，单模式类别一旦确定后就不再改变，称为谱系聚类法

依据准则函数动态聚类方法

设定一些分类的控制参数，定义一个表征聚类结构优劣的准则函数，聚类过程就是最优化函数取极值的优化过程

最大最小距离算法

设待分类 $\lbrace \mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n \rbrace$ ，选定比例系数 $\theta$
在模式特征矢量中以最大距离原则选取新的聚类中心，以最小距离原则进行模式归类，通常选择欧式距离

选任一模式特征矢量作为第一个聚类中心 $\mathbf{z}_1$
从待分类矢量集中选距离 $\mathbf{z}_1$ 最远的特征矢量作为第二个聚类中心
计算未被作为聚类中心的各模式特征矢量分别与 $\mathbf{z}_1,\mathbf{z}_2$ 之间的距离，对每一个模式计算一个当前距离聚类中心的最小值
在上方所有最小值中取一个最大值，判断是否大于 $\theta||\mathbf{z}_1 - \mathbf{z}_2||$ $θ ∣ ∣ z_{1} - z_{2} ∣ ∣$
1. 若大于，则作为第三个聚类中心
2. 如果等于，转第5步
3. 如果小于，转第6步
设存在 $k$ $k$ 个聚类中心，计算未被作为聚类中心的各特征矢量到各聚类中心的距离
1. 同理按照第4步进行计算
当判断不再有新的聚类中心之后，将剩余的模式按最小距离原则分到各类中去

谱系聚类法

见[学习笔记] - 多元统计分析 #简单连接

初始分类，每个模式自成一类
计算各类间的距离，生成一个对称的距离矩阵
找出最小的元素，合并为一类，产生新的聚类
重复上述步骤直到只有一类

动态聚类法

不是采用贪心算法等，被分类后的模式还可以继续改变

采用欧式距离：单纯计算距离
采用马氏距离：能反映出类的模式分布结构

建立初始聚类中心，进行初始聚类
计算模式和类的距离，调整模式的类别
计算各聚类的参数，删除，合并或分裂一些聚类
从初始聚类开始，运用迭代算法动态地改变模式的类别和聚类的中心使准则函数取得极值或设定的参数达到设计要求

            graph LR
            待分类模式-->产生初始聚类中心
产生初始聚类中心-->聚类
聚类-->检验聚类合理性
检验聚类合理性--不合理-->再迭代丨修改参数
再迭代丨修改参数-->聚类
检验聚类合理性--合理-->分类结果

C-均值法

取定 $C$ 个类别和选取 $C$ 个初始聚类中心，按最小距离原则将各模式分配到 $C$ 类中的某一类，之后不断地计算类心和调整各模式的类别，最终使各模式到其判属类别中心的距离平方之和最小。

任选C个模式特征向量作为初始聚类中心
将待分类的模式特征矢量集中的模式逐个按最小距离原则划分给 $C$ 类中的某一类
计算重新分类后的各类心
判断与上次计算类心是否相同，相同则结束，否则转到第2步

C-均值法分类结果容易受到类别数和初始聚类中心的影响，通常结果只是局部最优的，但是方法简单，结果差强人意，所以应用较多

类数 $c$ $c$ 的调整
- 利用先验知识选取
- 让类数递增重复进行聚类，选取 $J-c$ 曲线曲率变化最大点所对应的类数
初始聚类中心的选取课采取的方式
- 凭经验选取
- 将模式随机分为 $c$ 类计算每类内心
- 按密度大小选取
- 选取相距最远的 $c$ 个特征点
- 随机地选出 $c$ 个，用谱系聚类法聚成 $c$ 类，选取类心
- 由 $c-1$ 类问题，选取下一个最远的 $c$ 点

近邻函数法

在C-均值法中，当类内样本非球状散布时，用样本的均值矢量作为类的代表，一般聚类结果不佳，如果我们有类的模式分布的某些先验知识，可以构造能反映类的模式分布情况的核函数，那么就以核函数来代表类

如果实际中不能确定核函数或不能用简单的函数表示核函数时，可以采用临界函数法，这种算法特别适用于类的模式分布式条状或线状的情况

近邻函数：对于一个样本集中的任意两个样本 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ ，如果 $\mathbf{x}_i$ 是 $\mathbf{x}_j$ 的第 $i$ 个近邻点，则定义 $\mathbf{x}_i$ 对 $\mathbf{x}_j$ 的近邻系数为 $I$ ，记为 $d(i,j) = I$ ，如果 $\mathbf{x}_j$ 是 $\mathbf{x}_i$ 的第 $j$ 个近邻点，则定义 $\mathbf{x}_i$ 对 $\mathbf{x}_j$ 的近邻系数为 $J$ ，记为 $d(j,i) = J$ ，于是 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ 之间的近邻函数值定义为

a_{ij} = d(i,j) + d(j,i) - 2 = I + J - 2

当 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ 互为最近邻时，有 $a_{ij} = 0$ ，如果样本集包含 $N$ 个样本，那么近邻系数总是小于等于 $N-1$ ，因此 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ 之间的近邻函数值满足

a_{ij} \leq 2N - 4

连接损失：在聚类过程中，如果 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ 被聚为一类，就称 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ 是互相连接的，对于每个连接，都应定义一个指标，用以刻画这两个样本是狗适于连接，称其为连接损失

$a_{ij}$ 越小，表明它们越相似，把它们连接起来，损失也越小，所以 $a_{ij}$ 可作为连接损失
在聚类过程中，对于样本 $\mathbf{x}_i$ ，计算它与其他样本间的近邻函数数值，取最小把它们连接起来，并有连接损失 $a_{ik}$

类内连接损失：设有 $c$ 类，总的类连接损失定义为

L_w = \sum^c_{p=1}\sum a_{ij}

记 $\omega_j$ 类的类内最大近邻函数值

a_p = \max \lfloor a_{ij} \rfloor

设聚类 $\omega_p$ 和 $\omega_q$ 的样本之间的最小近邻函数值为 $r_{pq}$

r_{pq} = \min \lfloor a_{ij} \rfloor

设 $r_{pk}$ 聚类 $\omega_p$ 与其他各聚类的最小近邻函数值为 $r_{pq}$

r_{pk} = \min \lfloor r_{pq} \rfloor

上面表明，除 $\omega_p$ 类内样本外，只有 $\omega_k$ 中的某一个样本与 $\omega_p$ 中某一个样本最临界，近邻函数值为 $r_{pk}$

定义总的类间损失

L_B = \sum^c_{p=1}\beta_p

聚类的目标是使各 $r_{pk}$ 尽可能地大，使各 $a_p$ 尽可能的小，因而构造聚类的准则函数为

J_L = \min(L_w + L_B)

算法步骤

对于给定的待分类样本集，计算距离矩阵 $D$
利用矩阵 $D$ ，计算近邻矩阵 $M$ ，其元素 $M_{ij}$ 为样本 $\mathbf{x}$ 对 $\mathbf{x}$ 的近邻系数
生成近邻矩阵 $L$ ，其阵元为 $L_{ij} = M_{ij} + M_{ji} - 2$ ，置矩阵 $L$ 的主对角线上阵元 $L_{ii} = 2N$ ，如果 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ 有连接，则 $L_{ij}$ 给出它们非零近近邻函数值，即连接损失
搜索矩阵 $L$ ，将每个点与和它有最小近邻函数值的点连接起来，形成初始聚类
对于4.所形成的聚类，计算 $r_{pk}, a_{pm}, a_{km}$ ，若 $r_{pk}$ 小于或等于 $a_{pm}$ 或 $a_{km}$ ，则合并 $\omega_k$ 和 $\omega_p$ ，它们的样本间建立连接关系，转至5，否则结束

上诉过程将使 $J_L$ 最小

判别域代数界面方程法

判别域界面方差分类

原理：不同模式对应特征点在不同的区域中散布，运用已知类别的训练样本进行学习，产生若干个代数界面， $d(\mathbf{x})$ 将特征空间划分为一些互不重叠的子区域
判别函数：表示界面的函数 $d(\mathbf{x})$
线性可分：对于来自两类的一组模式，如果能用一个线性判别函数正确分类，则为线性可分

线性判别函数

在 $n$ 维特征空间中，特征矢量为 $\mathbf{x} = (x_1, x_2, \cdots, x_n)^T$ ，线性判别函数的一般形式为

\begin{aligned} d(\mathbf{x}) &= w_1x_1 + w_2x_2 + \cdots + w_nx_n + w_{n+1} \\ &= \mathbf{w}^T_0\mathbf{x} + w_{n+1} \end{aligned}

$\mathbf{w}_0$ 称为权矢量或系数矢量，简化为

\begin{aligned} d(\mathbf{x}) &= \mathbf{w}^T\mathbf{x} \\ \mathbf{x} &= (x_1, x_2, \cdots, x_n, 1)^T \\ \mathbf{w} &= (w_1, w_2, \cdots, w_n, w_{n+1})^T \end{aligned}

增广权矢量： $\mathbf{w}$
增广特征矢量： $\mathbf{x}$

线性判别两类问题

d(\mathbf{x}) \begin{cases} > 0 \rightarrow \mathbf{x} \in \omega_1 \\ < 0 \rightarrow \mathbf{x} \in \omega_2 \\ = 0 \rightarrow \text{拒判} \end{cases}

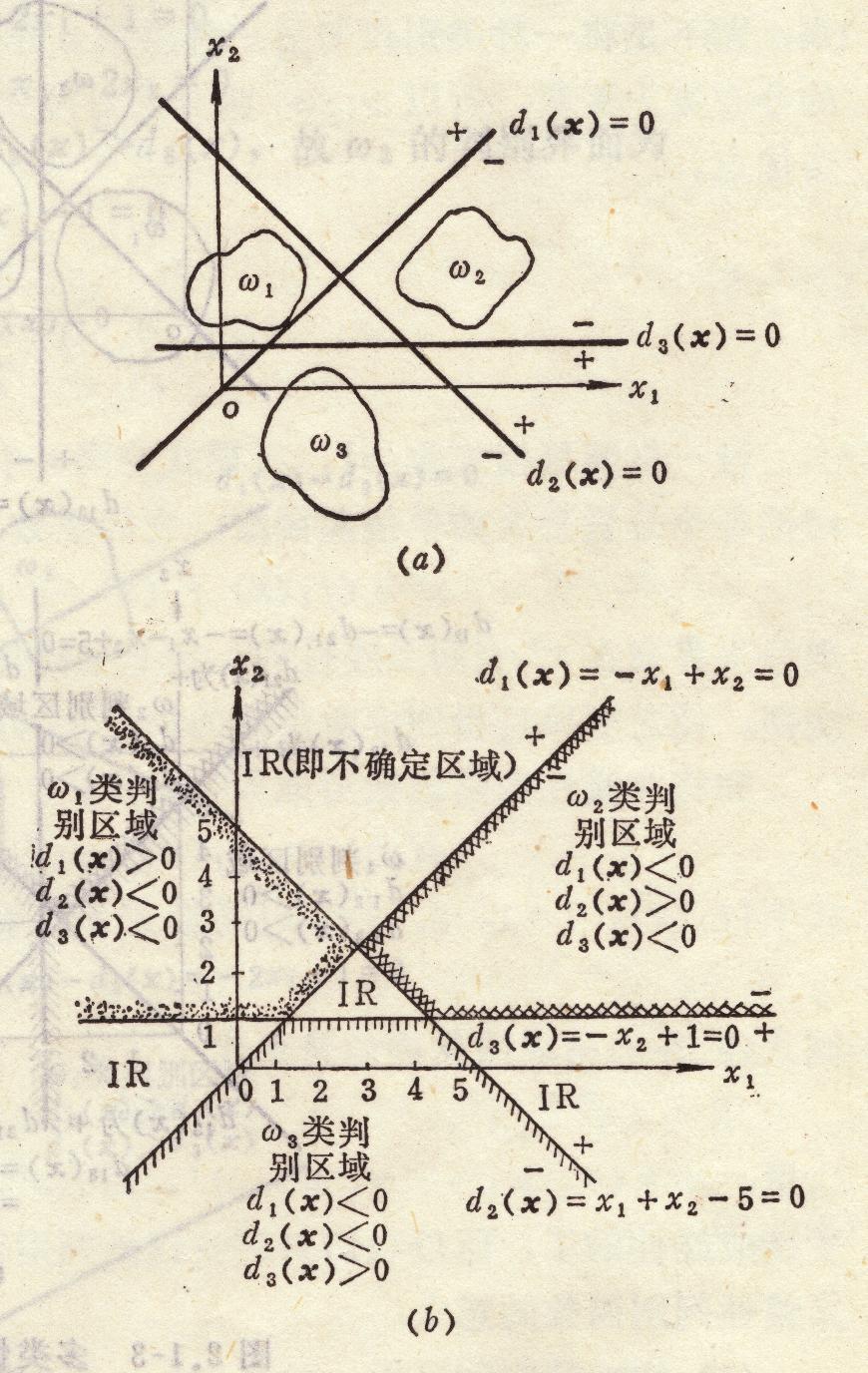
线性判别多类问题

$\omega_i/\overline{\omega}_i$ 两分法

将属于 $\omega_1$ 类和不属于 $\omega_i$ 类的模式分划开， $c$ 类问题转化为 $c - 1$ 个两类问题，可以建立 $c$ 个判别函数

d_i(\mathbf{x}) = \mathbf{w}_i^T\mathbf{x}, \quad i = 1,2,\cdots,c

通过训练，其中每个判别函数都具有下面的性质

d_i(\mathbf{x}) \begin{cases} > 0 & \mathbf{x} \in \omega_i \\ < 0 & \mathbf{x} \in \overline{\omega}_i \end{cases}

将 $\omega_i$ 和 $\overline{\omega}_i$ 类分开

$\omega_i/\omega_j$ 两分法

对于 $c$ 类中的任意两类 $\omega_i$ 和 $\omega_j$ 都分别建立一个判别函数，这个判别函数将属于 $\omega_i$ 的模式与属于 $\omega_j$ 的模式区分开，此函数对其他模式分类不提供信息，因此总共需要 $c(c-1)/2$ 个这样的判别函数，通过训练，区分 $i,j$ 两类的判别函数为

d_{ij}(\mathbf{x}) = \mathbf{w}_{ij}\mathbf{x}, \quad i,j = 1,2,\cdots,c,i\neq j

d_{ij}(\mathbf{x}) = \mathbf{w}_{ij}\mathbf{x} \begin{cases} > 0 & \mathbf{x} \in \omega_i \\ < 0 & \mathbf{x} \in \omega_j \end{cases}

具有性质 $d_{ij}(\mathbf{x}) = -d_{ji}(\mathbf{x})$ ，判别规则

d_{ij}(\mathbf{x}) > 0, \forall j\neq i \rightarrow x \in \omega_i

将 $\omega_i$ 和 $\omega_j$ 类分开

没有不确定区的 $\omega_i/\omega_j$ 两分法
令上面的判别函数为

d_{ij}(\mathbf{x}) = d_i(\mathbf{x}) - d_j(\mathbf{x}) = (w_i - w_j)^T\mathbf{x}

则 $d_{ij}(\mathbf{x}) > 0$ 等价于 $d_{i}(\mathbf{x}) > d_{j}(\mathbf{x})$ ，于是对每一类 $\omega_i$ 均建立一个判别函数 $d_i(\mathbf{x})$ ， $c$ 类问题又 $c$ 个判别函数

d_i(\mathbf{x}) = \mathbf{w}_i^T\mathbf{x},\quad i=1,2,\cdots,c

判别规则为：

d_i(\mathbf{x}) > d_j(\mathbf{x}),\quad \forall j \neq i \rightarrow \mathbf{x} \in \omega_i

或者写为

d_i(\mathbf{x}) = \max_{j} d_j(\mathbf{x}) \rightarrow \mathbf{x} \in \omega_i

判别函数值的鉴别意义

在 $n$ 维特征空间中，特征矢量维 $\mathbf{x} = (x_1, x_2, \cdots, x_n)^T$ ，线性判别函数的一般形式为

\begin{aligned} d(\mathbf{x}) &= w_1x_1 + w_2x_2 + \cdots + w_nx_n + w_{n+1} \end{aligned}

此方程表示一超平面，它具有以下性质

系数矢量： $\mathbf{w}_0 = (w_1, w_2, \cdots, w_n)^T$ 是该平面的法矢量
判别函数 $d(\mathbf{x})$ 的绝对值正比于 $\mathbf{x}$ 到超平面 $d(\mathbf{x}) = 0$ 距离
判别函数值的正负表示出特征点位于那个半空间中

权空间

增广特征矢量与增广权矢量是对称的，判别函数可以写成

d(\mathbf{x}) = \mathbf{w}^T\mathbf{x} = \mathbf{x}^T\mathbf{w} = x_1w_1+ x_2w_2 + \cdots + x_nw_n + w_{n+1}

这里 $x_1, x_2, \cdots, x_n, 1$ 则对应位相应的 $w_i$ 的权

$\mathbf{x}$ 指向平面 $\mathbf{x}^T\mathbf{w} = 0$ 的正侧，则该半空间中任一点 $\mathbf{w}$ 都使 $\mathbf{x}^T\mathbf{w} > 0$
$\mathbf{x}$ 背向平面 $\mathbf{x}^T\mathbf{w} = 0$ ，则该半空间中任一点 $\mathbf{w}$ 都使 $\mathbf{x}^T\mathbf{w} < 0$

解矢量

对于两类问题，在对待分类模式进行分类之前，应根据已知类别的增广训练模式，确认线性判别函数

d(\mathbf{x}) \mathbf{w}^T\mathbf{x}

当训练模式 $\mathbf{x}_j \in \omega_1 \rightarrow \mathbf{w}^T\mathbf{x}_j > 0$
当训练模式 $\mathbf{x}_j \in \omega_2 \rightarrow \mathbf{w}^T\mathbf{x}_j < 0$

此时的 $\mathbf{w}$ 称为解矢量，记为 $\mathbf{w}^*$ ，解矢量不是唯一的
可以把其中一类的符号转向，从而规范化为 $\mathbf{w}^T\mathbf{x}_j > 0$

解空间

$n$ 个训练模式将确定 $n$ 个界面，每个界面都把权空间分为两个半空间， $N$ 个正的半子空间的交空间使以权空间原点为顶点的凸多面锥

满足上式的个不等式 $\mathbf{w}$ 比在这个锥体中，锥体中每个点都是不等式的解，解矢量不是唯一的，上面的凸多面锥包含了解的全体，称为解空间

Fisher线性判别

见[学习笔记] - 多元统计分析 #判别分析和分类分析

线性可分条件下判别函数权矢量算法

感知器算法：用训练模式检验初始的或迭代中的增广权矢量 $\mathbf{w}$ 的合理性，当不合理时，对其进行校正
实质：校正方法实际上时最优化技术中的梯度下降法，本算法也是人工神经网络理论中的线性阈值神经元的学习算法

            graph TD
            任选一初始增广权矢量-->用训练样本检验分类是否正确
用训练样本检验分类是否正确--正确-->所有训练样本都正确分类
用训练样本检验分类是否正确--不正确-->对权值进行校正
对权值进行校正-->所有训练样本都正确分类
所有训练样本都正确分类--否-->用训练样本检验分类是否正确
所有训练样本都正确分类--是-->结束

设给定一个增广的训练模式集 $\lbrace \mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n \rbrace$ ，其中每个模式类别已知，它们分别属于 $\omega_1$ 类和 $\omega_2$ 类

置步数 $k=1$ ，令增量 $p = \text{某正常数}$ ，分别赋给初始增广权矢量 $\mathbf{w}(1)$ 的各分量较小的任意值
输入训练模式 $\mathbf{x}_k$ ，计算判别函数值 $\mathbf{w}^T(k)\mathbf{x}_k$
调整增广权矢量
1. 如果 $\mathbf{x}_k \in \omega_1$ 和 $\mathbf{w}^T(k)\mathbf{x}_k \leq 0$ ，则 $\mathbf{w}(k+1) = \mathbf{w}(k) + p\mathbf{x}_k$
2. 如果 $\mathbf{x}_k \in \omega_2$ 和 $\mathbf{w}^T(k)\mathbf{x}_k \geq 0$ ，则 $\mathbf{w}(k+1) = \mathbf{w}(k) - p\mathbf{x}_k$
3. 如果 $\mathbf{x}_k \in \omega_1$ 和 $\mathbf{w}^T(k)\mathbf{x}_k > 0$ ，或 $\mathbf{x}_k \in \omega_2$ 和 $\mathbf{w}^T(k)\mathbf{x}_k \leq 0$ ，则 $\mathbf{w}(k+1) = \mathbf{w}(k)$
如果 $k < N$ ，令 $k += 1$ ，返回2，如果 $k = N$ ，检验判别函数对所有模式是否正常分量，若是则结束，若不是，令 $k=1$ ，返回2

一般情况下的判别函数权矢量算法

如果线性不可分的情况，用线性分类的过程会不收敛
对线性不可分样本集，求一节矢量使得错分的模式数目最少

引入 $N$ 维余量矢量 $\mathbf{b} > \mathbf{\phi}$ ，不等式方程组变为

X\mathbf{w} \geq \mathbf{b} > \mathbf{\phi}

其中

X = \begin{pmatrix} \mathbf{x}^T_1 \\ \mathbf{x}^T_2 \\ \vdots \\ \mathbf{x}^T_N \end{pmatrix}

分段二次准则函数：

J(\mathbf{w}) = ||(X\mathbf{w} - \mathbf{b}) - |X\mathbf{w} - \mathbf{b}|||^2

在训练模式线性可分的情况下： $J(\mathbf{w}^* = 0)$
在训练模式线性不可分的情况下： $J(\mathbf{w}^* > 0)$ $J (w^{*} > 0)$
- 但可能使误分模式数最少

令 $\mathbf{s}_k$ 为寻求 $J(\mathbf{w})$ 极小值点的搜索方向
则共轭梯度法的基本公式为

\begin{aligned} \mathbf{g}_k &= \mathbf{g}(\mathbf{w}_k) = - \Delta J(\mathbf{w}_k) \\ \mathbf{s}_0 &= \mathbf{g}_0 \qquad \mathbf{s}_{k+1} &= \mathbf{g}_{k+1} + \beta_k\mathbf{s}_k \\ \beta_k &= \frac{\mathbf{g}^T_{k+1}\mathbf{g}_{k+1}}{\mathbf{g}^T_{k}\mathbf{g}_{k}} = \frac{||\mathbf{g}_{k+1}||}{||\mathbf{g}_{k}||} \\ \mathbf{v}_k &= J(\mathbf{w} + \mathbf{v}_k\mathbf{s}_k) = \min J(\mathbf{w}_k + \mathbf{v}\mathbf{s}_k) \\ \mathbf{w}_{k+1} &= \mathbf{w}_k + \mathbf{v}_k\mathbf{s}_k \end{aligned}

// TODO

非线性判别函数

设 $n$ 维模式特征集在特征空间 $\mathbf{x}^n$ 中是非线性可分的，对各模式作非线性变换

\begin{aligned} T&: X^n \rightarrow Y^d \quad d > n \\ \mathbf{x} &= (x_1, x_2, \cdots, x_n)^T\quad\mathbf{y} = (y_1, y_2, \cdots, y_n)^T \end{aligned}

其中 $y_i = f_i(\mathbf{x})$ 是 $\mathbf{x}$ 的单值函数，选取适当的函数

f_i(\mathbf{x}) \quad i = 1, 2, \cdots, d

使

\lbrace \mathbf{y}_j = (f_1(\mathbf{x}_j), f_2(\mathbf{x}_j), \cdots, f_d(\mathbf{x}_j)) \rbrace

在特征空间使线性可分的，称其维广义线性判别函数

// TODO

统计判决

贝叶斯判决进行分类时，要求满足以下两个条件

各类别总体的概率分布是已知的
要判决的类别数是一定的

先验概率：识别系统预先已知或者可以估计的模型属于某种类型的概率
$P(\omega_i)$ 表示类 $\omega_i$ 出现的先验概率，检测类 $\omega_i$ 的概率

P(\omega_1) + P(\omega_2) + \cdots + P(\omega_n) = 1

通常是整体的比例

类条件概率密度函数：模式样本 $\mathbf{x}$ 属于某类条件下出现的概率密度分布函数

P(\mathbf{x}|\omega_1)

后验概率：在某个具体的模式样本 $\mathbf{x}$ 条件下，该样本属于某种类型的概率。

P(\omega_1|\mathbf{x})

对模式识别来说，可以理解为： $\mathbf{x}$ 来自类 $\omega_i$ 的概率

后验概率涉及一个具体事务，而先验概率是泛指一类事物
后验概率可由贝叶斯公式计算，作为分类判决的依据

贝叶斯公式

P(\omega_i|\mathbf{x}) = \frac{P(\omega_i)P(\mathbf{x}|\omega_i)}{P(\mathbf{x})}

最小误判概率准则

对于两类 $\omega_1, \omega_2$ 问题，直观地，可以根据后验概率做判决

\begin{aligned} P(\omega_1|\mathbf{x}) > P(\omega_2|\mathbf{x}) \rightarrow \mathbf{x} \in \omega_1 \\ P(\omega_1|\mathbf{x}) < P(\omega_2|\mathbf{x}) \rightarrow \mathbf{x} \in \omega_2 \end{aligned}

我们再知道它是 $\mathbf{x}$ 的前提下，属于哪个类的几率大就判给谁

\begin{aligned} P(\mathbf{x}|\omega_1)P(\omega_1) > P(\mathbf{x}|\omega_2)P(\omega_2) \rightarrow \mathbf{x} \in \omega_1 \\ P(\mathbf{x}|\omega_1)P(\omega_1) < P(\mathbf{x}|\omega_2)P(\omega_2) \rightarrow \mathbf{x} \in \omega_2 \end{aligned}

在 $\omega_i$ 正确的情况下，谁属于 $\mathbf{x}$ 几率大就判给谁

\begin{aligned} l_{12} = \frac{P(\mathbf{x}|\omega_1)}{P(\mathbf{x}|\omega_2)} > \frac{P(\omega_2)}{P(\omega_1)} =\theta_{12} \rightarrow \mathbf{x} \in \omega_1 \\ l_{12} = \frac{P(\mathbf{x}|\omega_1)}{P(\mathbf{x}|\omega_2)} < \frac{P(\omega_2)}{P(\omega_1)} =\theta_{12} \rightarrow \mathbf{x} \in \omega_2 \end{aligned}

似然比： $l_{12}$
判决阈值： $\theta_{12}$

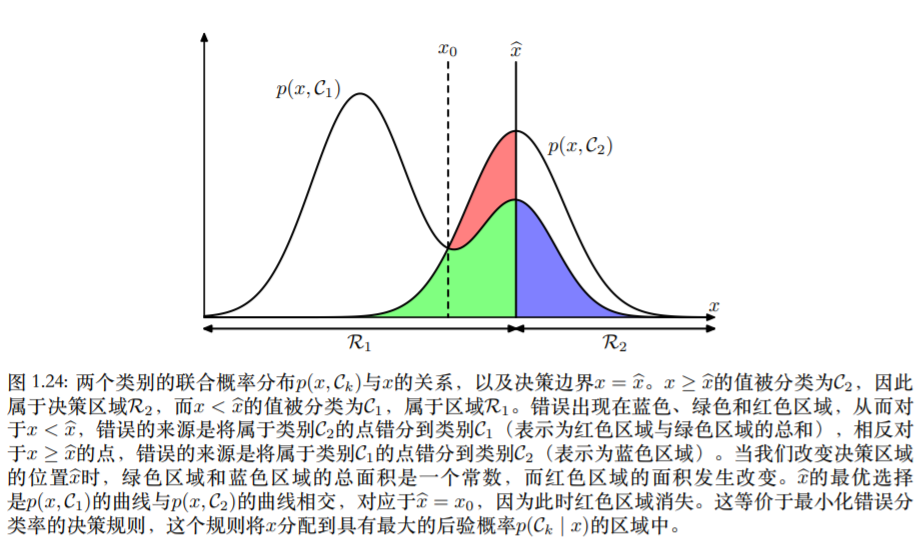
因为是按照几率判定的，所以可以由错误，在两类问题中

\begin{aligned} \varepsilon_{12} &= \int_{R_1}p(\mathbf{x}|\omega_1)\mathrm{d}\mathbf{x} \\ \varepsilon_{21} &= \int_{R_2}p(\mathbf{x}|\omega_2)\mathrm{d}\mathbf{x} \end{aligned}

设 $\omega_1$ 和 $\omega_2$ 类出现的概率分别问 $P(\omega_1)$ 和 $P(\omega_2)$ ，则总的误判概率是

\begin{aligned} P(e) &= P(\omega_1)\varepsilon_{12} + P(\omega_2)\varepsilon_{21} \\ &= P(\omega_1)\int_{R_1}p(\mathbf{x}|\omega_1)\mathrm{d}\mathbf{x} + P(\omega_2)\int_{R_2}p(\mathbf{x}|\omega_2)\mathrm{d}\mathbf{x} \end{aligned}

误判概率 $P(e)$ 最小等价于使正确分类概率 $P(c)$ 最大即

P(c) = \max\left (\int_{R_1}P(\omega_1)p(\mathbf{x}|\omega_1)\mathrm{d}\mathbf{x} + \int_{R_2}P(\omega_2)p(\mathbf{x}|\omega_2)\mathrm{d}\mathbf{x}\right )

因为

\int_{R_2}P(\omega_2)p(\mathbf{x}|\omega_2)\mathrm{d}\mathbf{x} = P(\omega_2) - \int_{R_1}p(\mathbf{x}|\omega_2)\mathrm{d}\mathbf{x}

所以

P(c) = \max\left (p(\omega_2) + \int_{R_1}\left [P(\omega_1)p(\mathbf{x}|\omega_1) - P(\omega_2)p(\mathbf{x}|\omega_2)\right ]\mathrm{d}\mathbf{x}\right )

为了使 $P(c)$ 最大， $R_1$ 是 $R$ 中所有满足条件

P(\omega_1)p(\mathbf{x}|\omega_1) > P(\omega_2)p(\mathbf{x}|\omega_2)

那些点 $\mathbf{x}$ 组成的集合

对于多类问题，最小误判概率准则有以下等价形式

后验概率形式
- 若 $P(\omega_i|\mathbf{x}) > P(\omega_j|\mathbf{x})$ ， $\forall j \neq i$ ，则判 $\mathbf{x} \in \omega_i$
- 若 $P(\omega_i|\mathbf{x}) = \max_j P(\omega_j|\mathbf{x})$ ，则判 $\mathbf{x} \in \omega_j$
条件概率形式
- 若 $P(\mathbf{x}|\omega_i)P(\omega_i) > P(\mathbf{x}|\omega_j)P(\omega_j)$ ， $\forall j \neq i$ ，则判 $\mathbf{x} \in \omega_i$
- 若 $P(\mathbf{x}|\omega_i)P(\omega_i) = \max_j P(\mathbf{x}|\omega_j)P(\omega_j)$ ，则判 $\mathbf{x} \in \omega_j$
似然比形式
- 若 $I_{ij}(\mathbf{x}) = \frac{p(\mathbf{x}|\omega_i)}{p(\mathbf{x}|\omega_j)} > \frac{P(\omega_j)}{P(\omega_i)}$ ，则判 $\mathbf{x} \in \omega_i$
条件概率的对数形式
- 如果 $\ln p(\mathbf{x}|\omega_i) + \ln P(\omega_i) > \ln p(\mathbf{x}|\omega_j) + \ln P(\omega_j)$ ， $\forall j \neq i$ ，则判 $\mathbf{x} \in \omega_i$

正态模式最小误判概率判决规则

在 $c$ 类问题中，属于 $\omega_i$ 类的 $n$ 维模式 $\mathbf{x}$ 的多变量正态分布密度函数为

p(\mathbf{x}|\omega_1) = \frac{1}{(2\pi)^{n/2}|\Sigma_i|^{1/2}}e^{-\frac{1}{2}(\mathbf{x} - \mathbf{\mu}_i)^T\Sigma^{-1}_i(\mathbf{x} - \mathbf{\mu}_i)}

均值向量： $\mathbf{\mu}_i = E_i(\mathbf{x})$
协方差矩阵： $\Sigma_i = E_i((\mathbf{x} - \mathbf{\mu}_i)(\mathbf{x} - \mathbf{\mu}_i)^T)$

$\omega_i$ 类的判决函数可以表示为

d_i(\mathbf{x}) = p(\mathbf{x}|\omega_i)P(\omega_i)

写成对数形式

d_i(\mathbf{x}) = \ln P(\omega_i) - \frac{n}{2}\ln(2\pi) - \frac{1}{2}\ln|\Sigma_i| - \frac{1}{2}(\mathbf{x} - \mathbf{\mu}_i)^T\Sigma^{-1}_i(\mathbf{x} - \mathbf{\mu}_i)

去掉不影响结果项后

d_i(\mathbf{x}) = \ln P(\omega_i) - \frac{1}{2}\ln|\Sigma_i| - \frac{1}{2}(\mathbf{x} - \mathbf{\mu}_i)^T\Sigma^{-1}_i(\mathbf{x} - \mathbf{\mu}_i)

判别规则： $d_i(\mathbf{x}) > d_j(\mathbf{x}) \rightarrow \mathbf{x} \in \omega_i$

若各类概率相等，可继续化简为马氏距离的平方

d_i(\mathbf{x}) = (\mathbf{x} - \mathbf{\mu}_i)^T\Sigma^{-1}(\mathbf{x} - \mathbf{\mu}_i)

$\mathbf{x}$ 属于马氏距离最小的那一类

当 $\Sigma_i = \Sigma$

则判决函数可以变换为

\begin{aligned} d_i(\mathbf{x}) &= \ln P(\omega_i) - \frac{1}{2}(\mathbf{x} - \mathbf{\mu}_i)^T\Sigma^{-1}_i(\mathbf{x} - \mathbf{\mu}_i) \\ &= \ln P(\omega_i) - \frac{1}{2}\mathbf{x}^T\Sigma^{-1}\mathbf{x} + \mathbf{\mu}^T\Sigma^{-1}\mathbf{x} - \frac{1}{2}\mathbf{\mu}^T\Sigma^{-1}\mathbf{\mu} \end{aligned}

当 $\Sigma_i \neq \Sigma$

这时一般的情况， $\omega_i$ 类模式的判决函数为

\begin{aligned} d_i(\mathbf{x}) &= \ln P(\omega_i) - \frac{1}{2}\ln|\Sigma_i| - \frac{1}{2}(\mathbf{x} - \mathbf{\mu}_i)^T\Sigma^{-1}_i(\mathbf{x} - \mathbf{\mu}_i) \\ &= -\frac{1}{2}\mathbf{x}^T\Sigma^{-1}_i\mathbf{x} + \mathbf{\mu}_i^T\Sigma^{-1}\mathbf{x}_i + \ln P(\omega_i) - \frac{1}{2}\ln|\Sigma_i| - \frac{1}{2}\mathbf{\mu}^T_i\Sigma^{-1}_i\mathbf{\mu}_i \end{aligned}

相邻两类的决策平面是超平面： $d_i(\mathbf{x}) - d_j(\mathbf{x}) = 0$

最小损失准则判决

设 $L_{ij}$ 为本来是属于 $\omega_i$ 类，但是判为 $\omega_j$ 类的损失
把 $\mathbf{x}$ 判为 $\omega_i$ 时的损失表示为

r(\omega_i|\mathbf{x}) = \sum^K_{k=1}L_{ik}P(\omega_i|\mathbf{x})

所以我们要选择损失最小的那一类

\argmin r(\omega_i|\mathbf{x})

这个时候的损失为

\begin{aligned} r &= E(r(\mathbf{x})) = \int_{\sum \omega_i} \min \left[ r(\omega_i|\mathbf{x}) \right] p(\mathbf{x}) \mathrm{d}\mathbf{x} \\ &= \int_{\omega_1} (\sum^K_{i=1} L_{1i} p(\mathbf{x}|\omega_1)P(\omega_1))\mathrm{d}\mathbf{x} \\ &+ \int_{\omega_2} (\sum^K_{i=1} L_{2i} p(\mathbf{x}|\omega_2)P(\omega_2))\mathrm{d}\mathbf{x} \\ &\vdots \\ &+ \int_{\omega_k} (\sum^K_{i=1} L_{ki} p(\mathbf{x}|\omega_k)P(\omega_k))\mathrm{d}\mathbf{x} \end{aligned}

参考

国防科技大学-模式识别（国家级精品课）

绪论