huhu's Blog

FLOWER ON THE PRECIPICE

[学习笔记] - 多元统计分析

发表于 更新于 分类于
本文字数： 56k 阅读时长 ≈ 51 分钟

多元统计分析是同时考量多个变量，从多元数据集种获取信息的统计方法

多元随机变量

现有nn个样本点，每个样本点包含pp个变量的观测，则数据集课表示为n×pn \times p矩阵

Y=(y11y12⋯y1py21y22⋯y2p⋮⋮⋱⋮yn1yn2⋯ynp)=(y1Ty2T⋮ynT)\mathbf{Y} = \begin{pmatrix} y_{11} & y_{12} & \cdots & y_{1p} \\ y_{21} & y_{22} & \cdots & y_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ y_{n1} & y_{n2} & \cdots & y_{np} \end{pmatrix} = \begin{pmatrix} \mathbf{y}^T_1 \\ \mathbf{y}^T_2 \\ \vdots \\ \mathbf{y}^T_n \end{pmatrix}

其中yi=(yi1,yi2,⋯ ,yip)\mathbf{y}_i = (y_{i1}, y_{i2}, \cdots, y_{ip})由Y\mathbf{Y}的第ii行构成，表示第ii个样本

均值向量

对于随机向量y=(yi1,yi2,⋯ ,yip)\mathbf{y} = (y_{i1}, y_{i2}, \cdots, y_{ip})

μ=E[y]=y‾=[E[y1]E[y2]⋯E[yn]]=∫ynyp(y)dy\mathbf{\mu} = E[\mathbf{y}] = \overline{\mathbf{y}} = \begin{bmatrix} E[y_1] \\ E[y_2] \\ \cdots \\ E[y_n] \end{bmatrix} = \int_{y^n} \mathbf{y}p(\mathbf{y})\mathrm{d}y

对于随机样本{y1,y2,⋯ ,yn}\lbrace \mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n \rbrace

y‾=1n∑i=1nyi=(y‾1,y‾2,⋯ ,y‾n)Ty‾i=1n∑i=1n,E(y‾)=u\begin{aligned} \overline{\mathbf{y}} &= \frac{1}{n}\sum^n_{i=1}\mathbf{y}_i = (\overline{y}_1, \overline{y}_2, \cdots, \overline{y}_n)^T \\ \\ \overline{y}_i &= \frac{1}{n}\sum^n_{i=1}, E(\overline{\mathbf{y}}) = \mathbf{u} \end{aligned}

协方差矩阵

对随机变量y=(Y1,Y2,⋯ ,Yp)T\mathbf{y} = (Y_1, Y_2, \cdots, Y_p)^T，p×pp \times p的总体协方差矩阵为

Σ=Cov(y)=E[(y−μ)(y−μ)T]=(σ11σ12⋯σ1pσ21σ22⋯σ2p⋮⋮⋱⋮σp1σp2⋯σpp)\Sigma = Cov(\mathbf{y}) = E[(\mathbf{y} - \mathbf{\mu})(\mathbf{y} - \mathbf{\mu})^T] = \begin{pmatrix} \sigma_{11} & \sigma_{12} & \cdots & \sigma_{1p} \\ \sigma_{21} & \sigma_{22} & \cdots & \sigma_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{p1} & \sigma_{p2} & \cdots & \sigma_{pp} \end{pmatrix}

σjk\sigma_{jk}为YjY_j和YkY_k之间的协方差

对随机样本{y1,y2,⋯ ,yn}\lbrace \mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n \rbrace，p×pp \times p的样本协方差矩阵为

S=1n−1∑i=1n(yi−y‾)(yi−y‾)T=(s11s12⋯s1ps21s22⋯s2p⋮⋮⋱⋮sp1sp2⋯spp)\mathbf{S} = \frac{1}{n-1}\sum^n_{i=1}(\mathbf{y}_i - \overline{\mathbf{y}})(\mathbf{y}_i - \overline{\mathbf{y}})^T = \begin{pmatrix} s_{11} & s_{12} & \cdots & s_{1p} \\ s_{21} & s_{22} & \cdots & s_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ s_{p1} & s_{p2} & \cdots & s_{pp} \end{pmatrix}

其中sij=1n−1∑i=1n(yij−y‾i)(yik−y‾k)s_{ij} = \frac{1}{n-1}\sum^n_{i=1}(y_{ij} - \overline{y}_i)(y_{ik} - \overline{y}_k)

  • Σ\Sigma和S\mathbf{S}是对称的
  • Σ\Sigma是S\mathbf{S}的无偏估计
  • y‾\overline{\mathbf{y}}的协方差矩阵是Cov(y‾)=ΣnCov(\overline{\mathbf{y}}) = \frac{\Sigma}{n}

总体相关系数矩阵

P=(pjk)=(1p12⋯p1pp211⋯p2p⋮⋮⋱⋮pp1pp2⋯1)\mathbf{P} = (p_{jk}) = \begin{pmatrix} 1 & p_{12} & \cdots & p_{1p} \\ p_{21} & 1 & \cdots & p_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ p_{p1} & p_{p2} & \cdots & 1 \end{pmatrix}

其中pjk=σjk/(σjσk)p_{jk} = \sigma_{jk}/(\sigma_j\sigma_k)为YiY_i与YjY_j之间的总体相关系数

对随机样本{y1,y2,⋯ ,yn}\lbrace \mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n \rbrace，样本相关系数矩阵为

R=(rjk)=(1r12⋯r1pr211⋯r2p⋮⋮⋱⋮rp1rp2⋯1)\mathbf{R} = (r_{jk}) = \begin{pmatrix} 1 & r_{12} & \cdots & r_{1p} \\ r_{21} & 1 & \cdots & r_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ r_{p1} & r_{p2} & \cdots & 1 \end{pmatrix}

其中rjk=sjk/sjjskk=sjk/(sjsk)r_{jk} = s_{jk}/\sqrt{s_{jj}s_{kk}} = s_{jk}/(s_{j}s_{k})为jj与kk个变量之间的样本相关系数

整体离散性

如果∣S∣|\mathbf{S}|很小，有可能是数据波动比较小，也可能是存在共线性现象，故∣S∣|\mathbf{S}|称为广义方程

tr(S)tr(\mathbf{S})刻画了各变量波动程度的总和，但忽略了变量间的相关性，故称总方差

去相关化

使相关系数矩阵除对角线之外的值全部为0叫做去相关化
协方差矩阵Σ\Sigma的特征值分别为

λ1,λ2,⋯ ,λp\lambda_1, \lambda_2, \cdots, \lambda_p

对应特征向量为

s1,s2,⋯ ,sp\mathbf{s}_1, \mathbf{s}_2, \cdots, \mathbf{s}_p

对Σ\Sigma进行矩阵的对角化，见[线性代数] - 矩阵的分解总结

Σ=SΛSΛ=STΣS\begin{aligned} \Sigma &= S\Lambda S \\ \Lambda &= S^T\Sigma S \end{aligned}

对随机样本{y1,y2,⋯ ,yn}\lbrace \mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n \rbrace，令Z=STYZ = S^TY，则Cov(Z)Cov(Z)为

Cov(Z)=Cov(STX)=E[(ST(X−μ))(ST(X−μ))T]=STE[(X−μ)(X−μ)T]S=STΣS=Σ\begin{aligned} Cov(Z) &= Cov(S^TX) \\ &= E\left [(S^T(X - \mu))(S^T(X - \mu))^T \right] \\ &= S^T E\left [(X - \mu)(X - \mu)^T \right] S \\ &= S^T\Sigma S \\ &= \Sigma \end{aligned}

标准化

N(0,1)∼ST(X−μ)ΛN(0, 1) \sim \frac{S^T(X - \mathbf{\mu})}{\sqrt{\Lambda}}

欧式距离

  • y1=(y11,y12,⋯ ,y1p)T\mathbf{y}_1 = (y_11, y_12, \cdots, y_1p)^T
  • y2=(y21,y22,⋯ ,y2p)T\mathbf{y}_2 = (y_21, y_22, \cdots, y_2p)^T

∣∣y1−y2∣∣=∑i=1n(y1i−y2i)2||\mathbf{y}_1 - \mathbf{y}_2|| = \sqrt{\sum^n_{i=1} (y_{1i} - y_{2i})^2}

欧式距离没有考虑到不同变量变化的尺度不同，以及变量之间的相关性

马氏距离

(y1−y2)TS−1(y1−y2)\sqrt{(\mathbf{y}_1 - \mathbf{y}_2)^T\mathbf{S}^{-1}(\mathbf{y}_1 - \mathbf{y}_2)}

通过添加协方差矩阵的逆，方差更大的变量贡献更小的权重，两个高度相关的变量的贡献小于俩个相关较低的变量

马氏距离就是把向量经过标准化之后的欧式距离(S−1/2y1,S−1/2y2\mathbf{S}^{-1/2}\mathbf{y}_1, \mathbf{S}^{-1/2}\mathbf{y}_2)

随机向量的变换

随机向量的分割

随机向量的分割

y=(Y1,Y2,⋯ ,Yp)T=(y(1)y(2))=(Y1Y2⋯YqYq+1Y2⋯Yp)\mathbf{y} = (Y_1, Y_2, \cdots, Y_p)^T = \begin{pmatrix} \mathbf{y}^{(1)} \\ \mathbf{y}^{(2)} \end{pmatrix} = \begin{pmatrix} Y_1 & Y_2 & \cdots & Y_q \\ Y_{q+1} & Y_2 & \cdots & Y_p \end{pmatrix}

于是y\mathbf{y}的总体协方差矩阵可以分割为

Σ=((Σ11)q×q(Σ12)q×(p−q)(Σ21)(p−q)×q(Σ22)(p−q)×(p−q))\Sigma = \begin{pmatrix} (\Sigma_{11})_{q\times q} & (\Sigma_{12})_{q\times (p-q)} \\ (\Sigma_{21})_{(p-q)\times q} & (\Sigma_{22})_{(p-q)\times (p-q)} \end{pmatrix}

  • Σ11\Sigma_{11}：是y(1)\mathbf{y}^{(1)}的协方差矩阵
  • Σ2\Sigma_{2}：是y(2)\mathbf{y}^{(2)}的协方差矩阵
  • Σ12=Σ21T\Sigma_{12} = \Sigma_{21}^T：包含了所有y(1)\mathbf{y}^{(1)}和y(2)\mathbf{y}^{(2)}元素两两之间协方差的矩阵，通常记作Cov(y(1),y(2))Cov(\mathbf{y}^{(1)}, \mathbf{y}^{(2)})

变量的线性组合

对y=(Y1,Y2,⋯ ,Yn)T\mathbf{y} = (Y_1, Y_2, \cdots, Y_n)^T的均值μ\mathbf{\mu}，协方差矩阵为Σ\Sigma

Z=aTy=∑j=1pajYj\begin{aligned} Z &= \mathbf{a}^T\mathbf{y} = \sum^p_{j=1}\mathbf{a}_jY_j \end{aligned}

其中a=(a1,a2,⋯ ,ap)\mathbf{a}=(a_1, a_2, \cdots, a_p)是系数向量

每个分量乘上一个常数，然后求和，转化为一维向量

  • E(Z)=E(aTy)=aTuE(Z) = E(\mathbf{a}^T\mathbf{y}) = \mathbf{a}^T\mathbf{u}
  • var(Z)=var(aTy)=aTΣavar(Z) = var(\mathbf{a}^T\mathbf{y}) = \mathbf{a}^T\Sigma\mathbf{a}

考虑2个线性组合

W=bTy=∑j=1pbjYjW = \mathbf{b}^T\mathbf{y} = \sum^p_{j=1}\mathbf{b}_jY_j

  • σZW=Cov(Z,W)=aTΣb\sigma_{ZW} = Cov(Z, W) = \mathbf{a}^T\Sigma\mathbf{b}
  • ρZW=corr(Z,W)=aTΣb(aTΣa)(bTΣb)\rho_{ZW} = corr(Z, W) = \frac{\mathbf{a}^T\Sigma\mathbf{b}}{\sqrt{(\mathbf{a}^T\Sigma\mathbf{a})(\mathbf{b}^T\Sigma\mathbf{b})}}

考虑qq个线性组合Y1,Y2,⋯ ,YpY_1, Y_2, \cdots, Y_p的线性组合，记为z=Ay\mathbf{z} = A\mathbf{y}，A=(aij)q×pA = (a_{ij})_{q\times p}，则

μz=E(Ay)=AμΣz=Cov(z)=AΣAT\begin{aligned} \mathbf{\mu}_z &= E(A\mathbf{y}) = A\mathbf{\mu} \\ \Sigma_z &= Cov(\mathbf{z}) = A\Sigma A^T \end{aligned}

更一般地，对于w=Ay+b\mathbf{w} = A\mathbf{y} + \mathbf{b}

μw=E(Ay+b)=Aμ+bΣw=Cov(w)=AΣAT\begin{aligned} \mathbf{\mu}_w &= E(A\mathbf{y} + b) = A\mathbf{\mu} + b \\ \Sigma_w &= Cov(\mathbf{w}) = A\Sigma A^T \end{aligned}

多元正态分布

若pp维随机变量y=(Y1,Y2,⋯ ,Yn)T\mathbf{y} = (Y_1, Y_2, \cdots, Y_n)^T服从均值向量为μ\mu，协方差矩阵为Σ\Sigma的多元正态分布，记为y∼Np(μ,Σ)\mathbf{y} \sim N_p(\mu, \Sigma)，则密度函数为

f(y)=1(2π)p/2∣Σ∣1/2e−(y−μ)TΣ−1(y−μ)2f(\mathbf{y}) = \frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}e^{-\frac{(\mathbf{y} - \mathbf{\mu})^T\Sigma^{-1}(\mathbf{y} - \mathbf{\mu})}{2}}

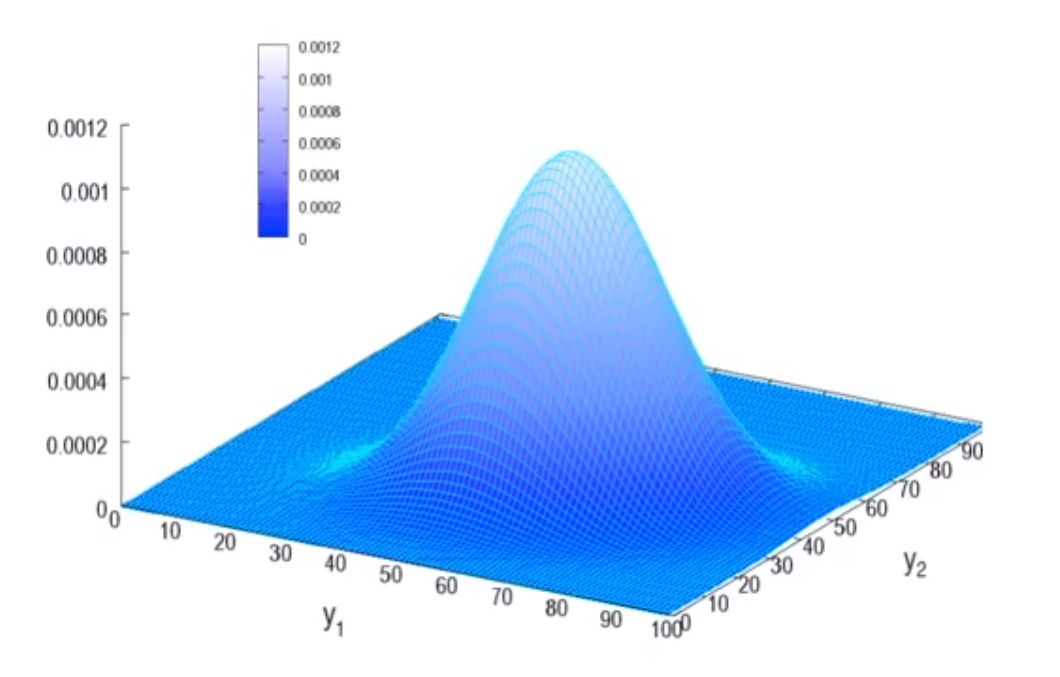
二元正态分布

p=2p = 2时，μ=(μ1μ2)\mathbf{\mu} = \begin{pmatrix}\mu_1\\\mu_2\end{pmatrix}，Σ=(σ12ρ12σ1σ2ρ21σ1σ2σ22)\Sigma = \begin{pmatrix} \sigma^2_1 & \rho_{12}\sigma_1\sigma_2\\\rho_{21}\sigma_1\sigma_2&\sigma_2^2\end{pmatrix}，所以随机向量y=(Y1,Y2)T\mathbf{y} = (Y_1, Y_2)^T服从二元正态分布，记为y∼BN(μ1,μ2,σ12,σ12,ρ12)\mathbf{y} \sim BN(\mu_1, \mu_2, \sigma^2_1, \sigma^2_1, \rho_{12})，密度函数为

f(y1,y2)=12πσ1σ2(1−ρ122)exp⁡[−(y1−y2σ1)2+(y2−μ2σ2)2−2ρ12(y1−μ1σ1)(y2−μ2σ2)2(1−ρ122)]f(y_1, y_2) = \frac{1}{2\pi \sigma_1\sigma_2\sqrt{(1 - \rho^2_{12})}} \exp\left[-\frac{(\frac{y_1 - y_2}{\sigma_1})^2 + (\frac{y_2 - \mu_2}{\sigma_2})^2 - 2\rho_{12}(\frac{y_1 - \mu_1}{\sigma_1})(\frac{y_2 - \mu_2}{\sigma_2})}{2(1 - \rho^2_{12})} \right]

如果2元的正态的分布的两个变量的相关系数为00，可以得出2个变量是独立的

二元正态分布等高线

概率密度等高线可表示为

(y1−y2σ1)2+(y2−μ2σ2)2−2ρ12(y1−μ1σ1)(y2−μ2σ2)=c12(\frac{y_1 - y_2}{\sigma_1})^2 + (\frac{y_2 - \mu_2}{\sigma_2})^2 - 2\rho_{12}(\frac{y_1 - \mu_1}{\sigma_1})(\frac{y_2 - \mu_2}{\sigma_2}) = c^2_1

若它们相关系数为00，则

(y1−y2c1σ1)2+(y2−μ2c1σ2)2=1(\frac{y_1 - y_2}{c_1\sigma_1})^2 + (\frac{y_2 - \mu_2}{c_1\sigma_2})^2 = 1

以y1y_1和y2y_2为中心轴的椭圆

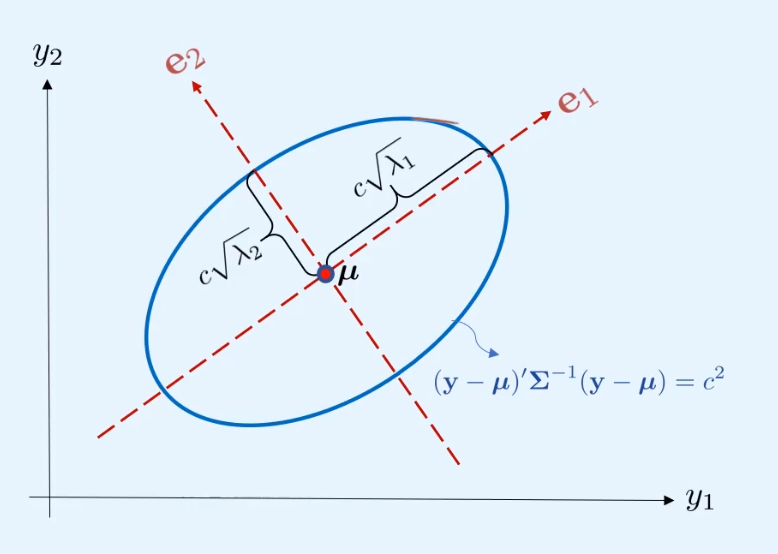
多元正态分布等高线

(y−μ)TΣ−1(y−μ)=c(\mathbf{y} - \mathbf{\mu})^T\Sigma^{-1}(\mathbf{y} - \mathbf{\mu})= c

通过矩阵的谱分解

Σ=∑j=1pλjejejT(λj,ej)为特征值-特征向量⇓Σ−1=∑j=1p1λjejejT\begin{gathered} \Sigma = \sum^p_{j=1}\lambda_je_je^T_j \quad (\lambda_j, e_j)\text{为特征值-特征向量} \\ \Downarrow \\ \Sigma^{-1} = \sum^p_{j=1}\frac{1}{\lambda_j}e_je^T_j \end{gathered}

代入原式后

∑j=1p(ejT(y−μ))2c2λj=1\sum^p_{j=1}\frac{(e^T_j(\mathbf{y} - \mathbf{\mu}))^2}{c^2\lambda_j} = 1

多元正态分布性质

多元正态分布的线性组合

Z=aTy=∑j=1pajYj\begin{aligned} Z &= \mathbf{a}^T\mathbf{y} = \sum^p_{j=1}\mathbf{a}_jY_j \end{aligned}

如果y∼Np(μ,Σ)\mathbf{y} \sim N_p(\mu, \Sigma)，则aTy∼N(aTμ,aTΣa)\mathbf{a}^T\mathbf{y} \sim N(\mathbf{a}^T\mathbf{\mu}, \mathbf{a}^T\Sigma\mathbf{a})
相对的，如果y\mathbf{y}中元素所有的线性组合都服从一元正态分布，则y\mathbf{y}一定是多元正态分布的

更一般地，假设AA是一个q×pq\times p且秩为q(≤p)q(\leq p)的常数矩阵，d\mathbf{d}为qq维常数向量，如果y∼Np(μ,Σ)\mathbf{y} \sim N_p(\mathbf{\mu}, \Sigma)，则

Ay+d∼Np(Aμ+d,AΣAT)A\mathbf{y} + \mathbf{d} \sim N_p(A\mathbf{\mu} + \mathbf{d}, A\Sigma A^T)

多元正态向量的分割

随机向量的分割

y=(Y1,Y2,⋯ ,Yp)T=(y(1)y(2))=(Y1Y2⋯YrYr+1Y2⋯Yp)\mathbf{y} = (Y_1, Y_2, \cdots, Y_p)^T = \begin{pmatrix} \mathbf{y}^{(1)} \\ \mathbf{y}^{(2)} \end{pmatrix} = \begin{pmatrix} Y_1 & Y_2 & \cdots & Y_r \\ Y_{r+1} & Y_2 & \cdots & Y_p \end{pmatrix}

总体协方差矩阵可以分割为

Σ=((Σ11)r×r(Σ12)r×(p−r)(Σ21)(p−r)×q(Σ22)(p−r)×(p−r))\Sigma = \begin{pmatrix} (\Sigma_{11})_{r\times r} & (\Sigma_{12})_{r\times (p-r)} \\ (\Sigma_{21})_{(p-r)\times q} & (\Sigma_{22})_{(p-r)\times (p-r)} \end{pmatrix}

如果y∼Np(μ,Σ)\mathbf{y} \sim N_p(\mu, \Sigma)，则它的子向量也服从正态分布

y1∼Nr(μ1,Σ11)y2∼Np−r(μ2,Σ22)\begin{aligned} \mathbf{y}_1 &\sim N_r(\mu_1, \Sigma_{11}) \\ \mathbf{y}_2 &\sim N_{p-r}(\mu_2, \Sigma_{22}) \end{aligned}

特别的，y=(Y1,Y2,⋯ ,Yn)T\mathbf{y} = (Y_1, Y_2, \cdots, Y_n)^T的第jj个元素服从一元正态分布

Yj∼N(μj,σjj)Y_j \sim N(\mu_j, \sigma_{jj})

多元正态向量的子向量条件分布

假设y∼Np(μ,Σ)\mathbf{y} \sim N_p(\mu, \Sigma)，并且∣Σ22∣>0|\Sigma_{22}| > 0，则对于其子向量y1\mathbf{y}_1和y2\mathbf{y}_2

y1∣y2∼Nr(μ1+Σ12Σ22−1(y2−μ2),Σ11−Σ12Σ22−1Σ21)\mathbf{y}_1|\mathbf{y}_2 \sim N_r(\mu_1 + \Sigma_{12}\Sigma^{-1}_{22}(\mathbf{y_2} - \mathbf{\mu}_2), \Sigma_{11} - \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21} )

  • 如果y\mathbf{y}是多元正态分布，则它的2个子向量有线性关系
    • 回归系数矩阵：Σ12Σ22−1\Sigma_{12}\Sigma^{-1}_{22}
  • Cov(y1∣y2)Cov(\mathbf{y}_1|\mathbf{y_2})不依赖y2\mathbf{y}_2

多元正态向量的独立性

考虑对于y,μ,Σ\mathbf{y}, \mathbf{\mu}, \Sigma的分割，假设y∼Np(μ,Σ)\mathbf{y} \sim N_p(\mathbf{\mu}, \Sigma)，则

  • y1\mathbf{y}_1和y2\mathbf{y}_2独立当且仅当Σ12=0\Sigma_{12} = \mathbf{0}
  • YjY_j和YkY_k独立当且仅当σjk=0\sigma_{jk} = 0

如果y1∼Nr(μ1,Σ11)\mathbf{y}_1 \sim N_r(\mathbf{\mu}_1, \Sigma_{11})，y2∼Np(μ2,Σ22)\mathbf{y}_2 \sim N_p(\mathbf{\mu}_2, \Sigma_{22})，且y1\mathbf{y}_1和y2\mathbf{y}_2相互独立，则

(y1y2)∼Nr+q[(μ1μ2),(Σ1100Σ22)]\begin{pmatrix} \mathbf{y}_1 \\ \mathbf{y}_2 \end{pmatrix} \sim N_{r+q}\left[\begin{pmatrix} \mathbf{\mu}_1 \\ \mathbf{\mu}_2 \end{pmatrix}, \begin{pmatrix} \Sigma_{11} & \mathbf{0} \\ \mathbf{0} & \Sigma_{22} \end{pmatrix}\right]

多元正态向量的和

如果y\mathbf{y}与x\mathbf{x}相互独立，并且

y∼Np(μy,Σyy)x∼Np(μx,Σxx)\begin{aligned} \mathbf{y} &\sim N_p(\mathbf{\mu_y}, \Sigma_{yy}) \\ \mathbf{x} &\sim N_p(\mathbf{\mu_x}, \Sigma_{xx}) \end{aligned}

则它们的和或差仍然服从正态分布

y±x∼Np(μy±μx,Σyy+Σxx)\mathbf{y} \pm \mathbf{x} \sim N_p(\mathbf{\mu_y} \pm \mathbf{\mu_x}, \Sigma_{yy} + \Sigma_{xx})

标准化多元正态向量

多元向量y\mathbf{y}的标准化向量定义为

z=(Σ)−1×(y−μ)z∼Np(0,I)\mathbf{z} = (\sqrt{\Sigma})^{-1} \times (\mathbf{y} - \mathbf{\mu}) \qquad \mathbf{z} \sim N_p(\mathbf{0}, \mathbf{I})

  • 基于谱分解

Σ=∑j=1pλjejejT⇓Σ=∑j=1pλjejejT\begin{gathered} \Sigma = \sum^p_{j=1}\lambda_je_je^T_j \\ \Downarrow \\ \sqrt{\Sigma} = \sum^p_{j=1}\sqrt{\lambda_j}e_je^T_j \end{gathered}

  • 基于Cholesky分解

Σ=TT→TTT=Σ\sqrt{\Sigma} = T^T \quad\rightarrow\quad T^TT=\Sigma

多元正态向量的二次型

如果y∼Np(μ,Σ)\mathbf{y} \sim N_p(\mu, \Sigma)，则标准化向量z∼Np(0,I)\mathbf{z} \sim N_p(\mathbf{0}, \mathbf{I})，则

zTz=∑j=1pZj2∼χ2(p)=(y−μ)TΣ−1(y−μ)\begin{aligned} \mathbf{z}^T\mathbf{z} &= \sum^p_{j=1}Z^2_j \sim \chi^2(p) \\ &= (\mathbf{y} - \mathbf{\mu})^T\Sigma^{-1}(\mathbf{y} - \mathbf{\mu}) \end{aligned}

即(y−μ)TΣ−1(y−μ)∼χ2(p)(\mathbf{y} - \mathbf{\mu})^T\Sigma^{-1}(\mathbf{y} - \mathbf{\mu}) \sim \chi^2(p)

多元正态分布的估计

极大似然估计多元正态分布

当y∼Np(μ,Σ)\mathbf{y} \sim N_p(\mu, \Sigma)，对μ\mathbf{\mu}和Σ\Sigma的估计通常由极大似然估计给出，给定独立同分布的nn个样本y1,y2,⋯ ,yn∼Np(μ,Σ)\mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n \sim N_p(\mathbf{\mu}, \Sigma)，其似然函数为

L(y1,y2,⋯ ,yn,μ,Σ)=∏i=1nf(yi,μ,Σ)=∏i=1n1(2π)p/2∣Σ∣1/2e−(y−μ)TΣ−1(y−μ)2=1(2π)np/2∣Σ∣n/2e−∑i=1n(y−μ)TΣ−1(y−μ)2\begin{aligned} L(\mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n, \mathbf{\mu}, \Sigma) &= \prod^n_{i=1}f(\mathbf{y}_i, \mathbf{\mu}, \Sigma) \\ &= \prod^n_{i=1}\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}e^{-\frac{(\mathbf{y} - \mathbf{\mu})^T\Sigma^{-1}(\mathbf{y} - \mathbf{\mu})}{2}} \\ &= \frac{1}{(2\pi)^{np/2}|\Sigma|^{n/2}}e^{-\sum^n_{i=1}\frac{(\mathbf{y} - \mathbf{\mu})^T\Sigma^{-1}(\mathbf{y} - \mathbf{\mu})}{2}} \end{aligned}

最大化似然函数LL来得到μ\mathbf{\mu}和Σ\Sigma的极大似然估计

step1. 确定分布律/分布函数PP
step2. 计算L(p)=∏i=inPL(p) = \prod^n_{i=i}P
step3. 计算ln⁡L(p)\ln{L(p)}
step4. 计算ddpln⁡L(p)=0\frac{d}{dp}\ln L(p) = 0，解出pp

见[数理统计] - 参数估计 #确定最大似然估计量

log⁡L(y1,y2,⋯ ,yn,μ,Σ)=log⁡∏i=1nf(yi,μ,Σ)=−n2log⁡∣Σ∣−12∑i=1n(yi−μ)TΣ−1(yi−μ)\begin{aligned} \log L(\mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n, \mathbf{\mu}, \Sigma) &= \log \prod^n_{i=1}f(\mathbf{y}_i, \mathbf{\mu}, \Sigma) \\ &= -\frac{n}{2} \log|\Sigma| - \frac{1}{2}\sum^n_{i=1}(\mathbf{y}_i - \mathbf{\mu})^T\Sigma^{-1}(\mathbf{y}_i - \mathbf{\mu}) \end{aligned}

我们先对μ\mathbf{\mu}进行极大化，对2次型求导为2倍的右边的部分

∂log⁡L∂μ=0=∑i=1nΣ−1(yi−μ)⇓μ^=1n∑i=1nyi=y‾\begin{gathered} \begin{aligned} \frac{\partial \log L}{\partial \mathbf{\mu}} &= \mathbf{0} \\ &= \sum^n_{i=1}\Sigma^{-1}(\mathbf{y}_i - \mathbf{\mu}) \end{aligned} \\ \Downarrow \\ \hat{\mathbf{\mu}} = \frac{1}{n}\sum^n_{i=1}\mathbf{y}_i = \overline{\mathbf{y}} \end{gathered}

现在对Σ\Sigma做极大似然估计，带入上面得到的μ^\hat{\mathbf{\mu}}

log⁡L(y1,y2,⋯ ,yn,μ,Σ)=log⁡∏i=1nf(yi,μ,Σ)=−n2log⁡∣Σ∣−12∑i=1n(yi−y‾)TΣ−1(yi−y‾)=−n2log⁡∣Σ∣−12∑i=1ntr(Σ−1(yi−y‾)(yi−y‾)T)=−n2log⁡∣Σ∣−12tr[Σ−1∑i=1n(yi−y‾)(yi−y‾)T]=−n2log⁡∣Σ∣−12tr(Σ−1S0)=n2log⁡∣Ω∣−12tr(ΩS0)\begin{aligned} \log L(\mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n, \mathbf{\mu}, \Sigma) &= \log \prod^n_{i=1}f(\mathbf{y}_i, \mathbf{\mu}, \Sigma) \\ &= -\frac{n}{2} \log|\Sigma| - \frac{1}{2}\sum^n_{i=1}(\mathbf{y}_i - \overline{\mathbf{y}})^T\Sigma^{-1}(\mathbf{y}_i - \overline{\mathbf{y}}) \\ &= -\frac{n}{2} \log|\Sigma| - \frac{1}{2}\sum^n_{i=1}tr(\Sigma^{-1}(\mathbf{y}_i - \overline{\mathbf{y}})(\mathbf{y}_i - \overline{\mathbf{y}})^T) \\ &= -\frac{n}{2} \log|\Sigma| - \frac{1}{2}tr\left[ \Sigma^{-1}\color{red}{\sum^n_{i=1}(\mathbf{y}_i - \overline{\mathbf{y}})(\mathbf{y}_i - \overline{\mathbf{y}})^T}\color{black} \right] \\ &= -\frac{n}{2} \log|\Sigma| - \frac{1}{2}tr(\color{red}\Sigma^{-1}\color{black}S_0) \\ &= \frac{n}{2} \log|\Omega| - \frac{1}{2}tr(\Omega S_0) \end{aligned}

tr(AB)=tr(BA)tr(AB) = tr(BA)

n2log⁡∣Ω∣−12tr(ΩS0)=n2log⁡∣ΩS0∣−12tr(ΩS0)−n2log⁡∣Ω∣\begin{aligned} \frac{n}{2} \log|\Omega| - \frac{1}{2}tr(\Omega S_0) = \frac{n}{2} \log|\Omega S_0| - \frac{1}{2}tr(\Omega S_0) - \frac{n}{2} \log|\Omega| \end{aligned}

S0S_0是已知值，假定λ1,λ2,⋯ ,λn\lambda_1, \lambda_2, \cdots, \lambda_n为ΩS0\Omega S_0的特征值，于是我们可以得到

n2log⁡∣Ω∣−12tr(ΩS0)=n2log⁡∏j=1pλj−12∑j=1pλj=12∑j=1p(nlog⁡λj−λj)\begin{aligned} \frac{n}{2} \log|\Omega| - \frac{1}{2}tr(\Omega S_0) &= \frac{n}{2} \log \prod^p_{j=1}\lambda_j - \frac{1}{2}\sum^p_{j=1}\lambda_j \\ &= \frac{1}{2} \sum^p_{j=1}(n\log \lambda_j - \lambda_j) \end{aligned}

现在实际上我们只需要对λj\lambda_j求极值即可，对每一个λj\lambda_j求偏导

∂log⁡L∂λj=0=12(nλj−1)⇓λj=n\begin{gathered} \begin{aligned} \frac{\partial \log L}{\partial \lambda_j} &= 0 \\ &= \frac{1}{2}(\frac{n}{\lambda_j} - 1) \end{aligned} \\ \Downarrow \\ \lambda_j = n \end{gathered}

如果一个矩阵的所有特征值都相等，则为单位矩阵×n\times n

ΩS0=n×Ip×p\Omega S_0 = n\times \mathbf{I}_{p\times p}

则可算出Σ^\hat{\Sigma}

Σ^=1nS0=1n∑i=1n(yi−y‾)(yi−y‾)T\hat{\Sigma} = \frac{1}{n}S_0 = \frac{1}{n}\sum^n_{i=1}(\mathbf{y}_i - \overline{\mathbf{y}})(\mathbf{y}_i - \overline{\mathbf{y}})^T

{μ^=1n∑i=1nyi=y‾Σ^=1nS0=1n∑i=1n(yi−y‾)(yi−y‾)T=n−1nS\begin{cases} \hat{\mathbf{\mu}} &= \frac{1}{n}\sum^n_{i=1}\mathbf{y}_i = \overline{\mathbf{y}} \\ \hat{\Sigma} &= \frac{1}{n}S_0 = \frac{1}{n}\sum^n_{i=1}(\mathbf{y}_i - \overline{\mathbf{y}})(\mathbf{y}_i - \overline{\mathbf{y}})^T = \frac{n - 1}{n}S \end{cases}

SS作为Σ\Sigma的估计是无偏的，而Σ^\hat{\Sigma}是有偏的，所以样本协方差矩阵SS在实际中更为常用

如果独立同分布多元样本{y1,y2,⋯ ,yn}\lbrace \mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n \rbrace来自Np(μ,Σ)N_p(\mathbf{\mu}, \Sigma)，则

  • 样本均值向量：y‾=∑i=1nyin\overline{\mathbf{y}} = \sum^n_{i=1}\frac{\mathbf{y}_i}{n}的分布为：y‾∼N(μ,Σ/n)\overline{\mathbf{y}} \sim N(\mathbf{\mu}, \Sigma/n)
  • 样本协方差矩阵S=1n−1∑i=1n(yi−μ)(yi−μ)TS = \frac{1}{n -1}\sum^n_{i=1}(\mathbf{y}_i - \mathbf{\mu})(\mathbf{y}_i - \mathbf{\mu})^T的分布为：(n−1)S∼Wp(n−1,Σ)(n-1)S \sim W_p(n - 1, \Sigma)
    • Wishart分布：卡方分布在多元情况下的推广
  • 在正态分布假设下，y‾\overline{\mathbf{y}}和SS相互独立

Wishart分布

假设pp维向量zi,i=1,2,⋯ ,q\mathbf{z}_i, i =1, 2, \cdots, q独立同分布且服从Np(0,Σ)N_p(0, \Sigma)，则

∑i=1pziziT∼Wp(q,Σ)\sum^p_{i=1}\mathbf{z}_i\mathbf{z}^T_i \sim W_p(q, \Sigma)

假设p×pp \times p随机矩阵W1W_1和W2W_2分别服从分布Wp(q1,Σ)W_p(q_1, \Sigma)，且Wp(q2,Σ)W_p(q_2, \Sigma)彼此独立，则

W1+W2∼Wp(q1+q2,Σ)W_1 + W_2 \sim W_p(q_1 + q_2, \Sigma)

如果W∼Wp(q,Σ)W \sim W_p(q, \Sigma)，CC为k×pk \times p的常数矩阵，则有

CWCT∼Wk(q,CΣCT)CWC^T \sim W_k(q, C\Sigma C^T)

评估正态性

  • 直方图
  • QQ图
    • 直线：正态
    • 反S形：比正态重尾
    • S形：比正态薄尾
    • 凸弯形：右偏
    • 凹弯形：左偏
  • 偏度，峰度=(0,3)= (0, 3)

拟合优度检验：检验数据是否来自一种特定的分布

H0:数据来自正态分布H1:数据不来自正态分布\begin{aligned} H_0&: \text{数据来自正态分布} \\ H_1&: \text{数据不来自正态分布} \end{aligned}

Shapiro-Wilks检验

检验统计量：

W=(∑i=1na(i)y(i))2∑i=1n(yi−y‾)2W = \frac{(\sum^n_{i=1}a_{(i)y_{(i)}})^2}{\sum^n_{i=1}(y_i-\overline{y})^2}

  • y(i)y_{(i)}：第ii个样本次序统计量
  • a(i)a_{(i)}：标准正态分布中第ii个标准化次序统计量

W\sqrt{W}可看作实际数据与正态数据之间的相关系数

  • 当W=1W = 1时，数据为正态分布
  • WW显著小于11则表明数据非正态

Kolmogorov-Smirnov检验

D=nsup⁡y∣Fn(y)−F0(y)∣D = \sqrt{n}\sup_{y}|F_n(y) - F_0(y)|

  • Fn(y)F_n(y)：是数据的经验累积分布函数
  • F0(y)F_0(y)：是与数据同均值，同方差的正态分布的累积分布函数

结果

  • 当DD值很大时，则拒绝原假设H0H_0

Cramer-von Miss检验

C=∫[Fn(y)−F0(y)]2dF0(y)C = \int [F_n(y) - F_0(y)]^2 \mathrm{d}F_0(y)

  • Fn(y)F_n(y)：是数据的经验累积分布函数
  • F0(y)F_0(y)：是与数据同均值，同方差的正态分布的累积分布函数

结果

  • 当CC值很大时，则拒绝原假设H0H_0

Anderson-Darling检验

A=∫[Fn(y)−F0(y)]2F0(y)(1−F0(y))dF0(y)A = \int \frac{[F_n(y) - F_0(y)]^2}{F_0(y)(1 - F_0(y))}\mathrm{d}F_0(y)

相对于Cramer-von Miss检验给予尾巴上的数据更大的权重

多元数据的正态性

  • 检验向量的每一维是否都是一元正态分布
  • 检验是否成对散点图存在非线性趋势
  • 构造χ2\chi^2QQ图，检验统计距离{d1,d2,⋯ ,dn}\lbrace d_1, d_2, \cdots, d_n \rbrace是否距离χ2(p)\chi^2(p)很远
    • 其中di(yi−y‾)TS−1(yi−y‾)d_i(\mathbf{y}_i - \overline{\mathbf{y}})^TS^{-1}(\mathbf{y}_i - \overline{\mathbf{y}})

均值向量的检验

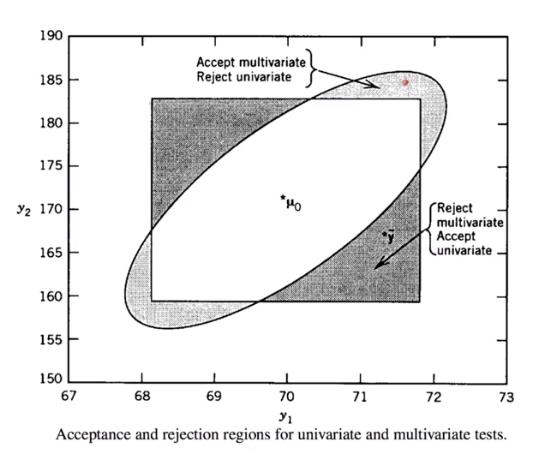
多元检验的动机

  • 多元数据的单样本检验问题
  • 两样本多元数据的检验

如果对每一维度分布进行一元检验，则每次一都aa几率犯第一类错误。一元检验有时会降低统计功效，小的个体效应可能累积称为显著的联合效应，也就是说每个差异都很小，但是累积起来就会非常的大，导致多元检验下会拒绝原假设，但是一维检验全部接受

单样本均值向量检验

p\mathbf{p}维独立同分布的样本{y1,y2,⋯ ,yn}\lbrace \mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n \rbrace服从Np(μ,Σ)N_p(\mathbf{\mu}, \Sigma)分布，其中

  • 未知：μ\mathbf{\mu}
  • 已知：Σ\Sigma

待检验问题

H0:μ=μ0H1:μ≠μ0\begin{aligned} H_0&: \mu = \mu_0 \\ H_1&: \mu \neq \mu_0 \end{aligned}

检验统计量：马氏距离（因为是向量）

Z2=n(y‾−μ0)TΣ−1(y‾−μ0)Cov(y‾)=Σ/nZ^2 = n(\overline{\mathbf{y}} - \mathbf{\mu}_0)^T\Sigma^{-1}(\overline{\mathbf{y}} - \mathbf{\mu}_0) \quad Cov(\overline{\mathbf{y}}) = \Sigma/n

统计量原假设分布

Z2=n(y‾−μ0)TΣ−1(y‾−μ0)∼χ2(p)p:样本维度Z^2 = n(\overline{\mathbf{y}} - \mathbf{\mu}_0)^T\Sigma^{-1}(\overline{\mathbf{y}} - \mathbf{\mu}_0) \sim \chi^2(p) \quad p: \text{样本维度}

拒绝域

Z2>χa2(p)Z^2 > \chi^2_a(p)

在几何上，如果点落在椭圆里面，则接受

因为数据来自二元，一元会忽略掉变量之间的关系，二元的假设检验的结论更加可信

p\mathbf{p}维独立同分布的样本{y1,y2,⋯ ,yn}\lbrace \mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n \rbrace服从Np(μ,Σ)N_p(\mathbf{\mu}, \Sigma)分布，其中

  • 未知：μ\mathbf{\mu}
  • 未知：Σ\Sigma

待检验问题

H0:μ=μ0H1:μ≠μ0\begin{aligned} H_0&: \mu = \mu_0 \\ H_1&: \mu \neq \mu_0 \end{aligned}

检验统计量：Hotelling T平方检验统计量
把Σ\Sigma替换为样本协方差矩阵

T2=n(y‾−μ0)TS−1(y‾−μ0)T^2 = n(\overline{\mathbf{y}} - \mathbf{\mu}_0)^TS^{-1}(\overline{\mathbf{y}} - \mathbf{\mu}_0)

统计量原假设分布：Hotelling T分布

T2∼T2(p,n−1){p:样本维度n:样本个数T^2 \sim T^2(p, n -1) \quad \begin{cases} p: \text{样本维度} \\ n: \text{样本个数} \end{cases}

拒绝域

T2>Ta2(p,n−1)T^2 > T^2_a(p, n - 1)

Hotelling T分布可以转化为F分布

n−pp(n−1)T2(p,n−1)=F(p,n−p)\frac{n - p}{p(n - 1)}T^2(p,n - 1) = F(p,n-p)

两样本均值向量检验

独立两样本均值向量检验

假设群体1与群体2之间是独立的，假设

  • y11,y12,⋯ ,y1n1y_{11}, y_{12}, \cdots, y_{1n_1} 来自 N(μ1,Σ)N(\mu_1, \Sigma)
  • y21,y22,⋯ ,y2n2y_{21}, y_{22}, \cdots, y_{2n_2} 来自 N(μ2,Σ)N(\mu_2, \Sigma)

我们需要检验它们的均值是否相等

  • 单边检验
    • H0:μ1=μ2H_0: \mathbf{\mu}_1 = \mathbf{\mu}_2或μ1≤μ2\mathbf{\mu}_1 \leq \mathbf{\mu}_2
    • H1:μ1>μ2H_1: \mathbf{\mu}_1 > \mathbf{\mu}_2
  • 单边检验
    • H0:μ1=μ2H_0: \mathbf{\mu}_1 = \mathbf{\mu}_2或μ1≥μ2\mathbf{\mu}_1 \geq \mathbf{\mu}_2
    • H1:μ1<μ2H_1: \mathbf{\mu}_1 < \mathbf{\mu}_2
  • 双边验
    • H0:μ1=μ2H_0: \mathbf{\mu}_1 = \mathbf{\mu}_2
    • H1:μ1≠μ2H_1: \mathbf{\mu}_1 \neq \mathbf{\mu}_2

不知道μ\mathbf{\mu}就用y‾\overline{\mathbf{y}}来估计它

检验统计量，若Cov(y‾1,y‾2)=Σ(1n2+1n2)Cov(\overline{\mathbf{y}}_1, \overline{\mathbf{y}}_2) = \Sigma(\frac{1}{n_2} + \frac{1}{n_2})协方差已知，则使用，否则用SplS_{pl}来替代

T2=n1n2n1+n2(y‾1−y‾2)TSpl−1(y‾1−y‾2)Spl=(n1−1)S1+(n2−1)S2n1+n2−2\begin{aligned} T^2 &= \frac{n_1n_2}{n_1 + n_2}(\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2)^TS^{-1}_{pl}(\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2) \\ S_{pl} &= \frac{(n_1 - 1)S_1 + (n_2 - 1)S_2}{n_1 + n_2 - 2} \end{aligned}

本质也是估计y‾1\overline{\mathbf{y}}_1和y‾2\overline{\mathbf{y}}_2的马氏距离

统计量原假设分布：

T2∼T2(p,n1+n2−2)T^2 \sim T^2(p, n_1 + n_2 - 2)

拒绝域

T2>Ta2(p,n1+n2−2)T^2 > T^2_a(p, n_1 + n_2 - 2)

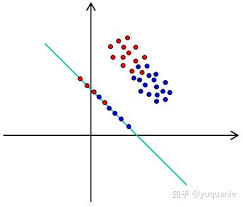
Fisher判别函数法可以用来寻找两个群体间"最好"的线性组合法则，来最大限度地区分两个群体

成对两样本均值向量检验

成对样本：群体1与群体2之间是成对的

  • y11,y12,⋯ ,y1n1y_{11}, y_{12}, \cdots, y_{1n_1} 来自 N(μ1,Σ)N(\mu_1, \Sigma)
  • y21,y22,⋯ ,y2n2y_{21}, y_{22}, \cdots, y_{2n_2} 来自 N(μ2,Σ)N(\mu_2, \Sigma)

由于是成对出现的，差异di=yi−xi\mathbf{d}_i = \mathbf{y}_i - \mathbf{x}_i独立同分布服从于Np(λ,Σd)N_p(\mathbf{\lambda}, \Sigma_d)，其中λ=μy=μx\mathbf{\lambda} = \mathbf{\mu}_y = \mathbf{\mu}_x
参数估计

  • λ\mathbf{\lambda}的估计：d‾=∑i=1ndi\overline{\mathbf{d}} = \sum^n_{i=1}\mathbf{d}_i
  • Σd\Sigma_d的估计：Sd=Σi=1n(di−d‾)(di−d‾)Tn−1S_d = \frac{\Sigma^n_{i=1}(\mathbf{d}_i - \overline{\mathbf{d}})(\mathbf{d}_i - \overline{\mathbf{d}})^T}{n - 1}

待检验问题

H0:λ=0H1:λ≠0\begin{aligned} H_0&: \mathbf{\lambda} = \mathbf{0} \\ H_1&: \mathbf{\lambda} \neq \mathbf{0} \end{aligned}

检验统计量及其原假设分布

T2nd‾Sd−1d‾∼T2(p,n−1)T^2 n\overline{\mathbf{d}}S^{-1}_d\overline{\mathbf{d}} \sim T^2(p, n - 1)

拒绝域

T2>Ta2(p,n−1)T^2 > T^2_a(p, n - 1)

判别分析和分类分析

  • 判别分析：寻找一种判别规则，利用变量的函数（判别函数）来描述，解释两组或多组群体间的区别
    • 寻找分类的规则
  • 分类分析：预测一个新观察对象的类别-利用判别函数在新观测上的取值，找到该观测最有可能属于的类别
    • 给出分类的结果

最终目的通常都是分类

判别分析和分类分析中，所有个体有既定标签，即有：标准答案可供监督，所以为有监督学习

判别分析

Fisher’s LDA 贝叶斯法则
不需要分布假设 需要明确f(y1)f(\mathbf{y}_1)和f(y2)f(\mathbf{y}_2)
需要同协方差矩阵假设 不要求同协方差矩阵假设
不可以考虑先验概率和误判代价 可以考虑先验概率和误判代价

两群体Fisher线性判别分析

用来寻找两个群体间"最好"的线性组合法则，来最大限度地区分两个群体
假设：
两个群体的均值向量μ1≠μ2\mathbf{\mu}_1 \neq \mathbf{\mu}_2，但具有相同的协方差矩阵Σ\Sigma
随机样本：

  • y11,y12,⋯ ,y1n1y_{11}, y_{12}, \cdots, y_{1n_1}
    • 样本均值向量y‾1\overline{\mathbf{y}}_1
    • 协方差矩阵：Σ/n1\Sigma/n_1
  • y21,y22,⋯ ,y2n2y_{21}, y_{22}, \cdots, y_{2n_2}
    • 样本均值向量y‾2\overline{\mathbf{y}}_2
    • 协方差矩阵：Σ/n2\Sigma/n_2

线性组合法则：实际上是投影方向，往一条直线投影

但是我们不需要看所有的点，而是让它们的样本均值投影后之间的距离最大，找到一个a\mathbf{a}方向，其中y‾1\overline{\mathbf{y}}_1和y‾2\overline{\mathbf{y}}_2在其的投影长度为Z‾1=aTy‾1\overline{Z}_1 = \mathbf{a}^T\overline{\mathbf{y}}_1和Z‾2=aTy‾2\overline{Z}_2 = \mathbf{a}^T\overline{\mathbf{y}}_2，我们需要找到一个a\mathbf{a}使得d=Z‾1−Z‾2d = \overline{Z}_1 - \overline{Z}_2最大，但是这是欧式距离，可能只是单纯的它本身比较大，所以需要寻找它们标准化后的距离的最大

Cov(y‾1−y‾2)=Σ(1n1+1n2)⇓var(d)=(1n1+1n2)aTΣasd=(1n1+1n2)aTSpla\begin{gathered} Cov(\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2) = \Sigma(\frac{1}{n_1} + \frac{1}{n_2}) \\ \Downarrow \\ var(d) = (\frac{1}{n_1} + \frac{1}{n_2})\mathbf{a}^T\Sigma\mathbf{a} \\ s_d = \sqrt{(\frac{1}{n_1} + \frac{1}{n_2})\mathbf{a}^TS_{pl}\mathbf{a}} \end{gathered}

得到我们最终要最大化的标准化距离

t2(a)=(dsd)2=(aT(y‾1−y‾2))2(1n1+1n2)aTSplat^2(\mathbf{a}) = (\frac{d}{s_d})^2 = \frac{(\color{red}\mathbf{a}^T\color{black}(\color{blue}\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2\color{black}))^2}{\color{grey}(\frac{1}{n_1} + \frac{1}{n_2})\color{black}\color{red}\mathbf{a}^T\color{black}\color{green}S_{pl}\color{black}\color{red}\mathbf{a}}

Fisher线性判别分析寻找a\mathbf{a}使得t2(a)t^2(\mathbf{a})最大

柯西不等式

(aTb)2≤(aTa)(bTb)≤(aTWa)(bTW−1b)(aTb)2aTWa≤bTW−1b(=→a=W−1b)\begin{aligned} (\mathbf{a}^T\mathbf{b})^2 &\leq (\mathbf{a}^T\mathbf{a})(\mathbf{b}^T\mathbf{b}) \\ &\leq (\mathbf{a}^TW\mathbf{a})(\mathbf{b}^TW^{-1}\mathbf{b}) \\ \frac{(\mathbf{a}^T\mathbf{b})^2}{\mathbf{a}^TW\mathbf{a}} &\leq \mathbf{b}^TW^{-1}\mathbf{b} \quad (= \rightarrow \mathbf{a} = W^{-1}\mathbf{b}) \end{aligned}

所以为了使t2(a)t^2(\mathbf{a})最大，则

a=Spl−1(y‾1−y‾2)\mathbf{a} = S_{pl}^{-1}(\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2)

称为判别函数系数

z=aTy\mathbf{z} = \mathbf{a}^T\mathbf{y}

称为Fisher判别函数

多群体Fisher线性判别分析

现有gg个群体Gk,k=1,2,⋯ ,gG_k, k =1, 2, \cdots, g

  • 第kk个群体样本为：yk1,yk2,⋯ ,yknk\mathbf{y}_{k1}, \mathbf{y}_{k2}, \cdots, \mathbf{y}_{kn_k}
  • 第kk个群体样本容量为：nkn_k
  • 第kk个群体样本均值为：y‾k\overline{\mathbf{y}}_k
  • s所有群体均值为y‾=1/g∑k=1gy‾k\overline{\mathbf{y}} = 1/g\sum^g_{k=1}\overline{\mathbf{y}}_k

目标函数：多群体“组间方差”和“组内方差”的比值为

aTBaaTW−1a=aT[∑k=1g(y‾k−y‾)]aaT[∑k=1g∑i=1nk(yki−y‾k)(yki−y‾k)T]a\frac{\mathbf{a}^TB\mathbf{a}}{\mathbf{a}^TW^{-1}\mathbf{a}} = \frac{\mathbf{a}^T[\color{red}\sum^g_{k=1}(\overline{\mathbf{y}}_k - \overline{\mathbf{y}})\color{black}]\mathbf{a}}{\mathbf{a}^T[\color{green}\sum^g_{k=1}\sum^{n_k}_{i=1}(\mathbf{y}_{ki} - \overline{\mathbf{y}}_k)(\mathbf{y}_{ki} - \overline{\mathbf{y}}_k)^T\color{black}]\mathbf{a}}

将矩阵W−1BW^{-1}B的非零特征值记为λ1,λ2,⋯ ,λs>0\lambda_1, \lambda_2, \cdots, \lambda_s > 0，其中s≤min⁡(g−1,p)s \leq \min(g - 1, p)，对应的特征向量为e1,e2,⋯ ,es\mathbf{e}_1, \mathbf{e}_2, \cdots, \mathbf{e}_s，则a=e1\mathbf{a} = \mathbf{e}_1为最大化的系数向量，对应最大值为λ1\lambda_1

  • 样本第一判别式：线性组合e1Ty\mathbf{e}^T_1 \mathbf{y}
  • 样本第二判别式：线性组合e2Ty\mathbf{e}^T_2 \mathbf{y}
  • …

有多少e\mathbf{e}，就有多少判别式，最多g−1g-1

分类分析

判别分析旨在寻找一种分类规则，而分类分析更进一步：将新观测对象分到一个合适的类别-即在分析过程中的预测部分

两群体Fisher分类

根据距离均值向量的距离大小进行分类
如果

(y‾1−y‾2)TSpl−1y0≥12(y‾1−y‾2)TSpl−1(y‾1+y‾2)(\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2)^TS^{-1}_{pl}\mathbf{y}_0 \geq \frac{1}{2}(\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2)^TS^{-1}_{pl}(\overline{\mathbf{y}}_1 + \overline{\mathbf{y}}_2)

则将新观测对象y0\mathbf{y}_0分为类别G1G_1，如果

(y‾1−y‾2)TSpl−1y0<12(y‾1−y‾2)TSpl−1(y‾1+y‾2)(\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2)^TS^{-1}_{pl}\mathbf{y}_0 < \frac{1}{2}(\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2)^TS^{-1}_{pl}(\overline{\mathbf{y}}_1 + \overline{\mathbf{y}}_2)

则将新观测对象y0\mathbf{y}_0分为类别G2G_2

Fisher分类实际是在比较新观测对象y0\mathbf{y}_0与y‾1,y‾2\overline{\mathbf{y}}_1, \overline{\mathbf{y}}_2间的马氏距离

真实数据中，任何分类法则通常都不能完全正确地分类，可用以下表格计算总错分率

G1G1 G2G2
G1G1 n11n_{11} ×n12\times n_{12}
G2G2 ×n21\times n_{21} n22n_{22}

TPM=P(样本被分为G1实际上来自G2)+P(样本被分为G2实际上来自G1)=n12+n21n11+n12+n21+n22\begin{aligned} \text{TPM} &= P(\text{样本被分为}G_1\text{实际上来自}G_2) + P(\text{样本被分为}G_2\text{实际上来自}G_1) \\ &= \frac{n_{12} + n_{21}}{n_{11} + n_{12} + n_{21} + n_{22}} \end{aligned}

Fisher分类是线性的，在非线性问题中就失效了

两群体贝叶斯分类

G1G_1和G2G_2代表两个总体，各自的先验概率为p1p_1和p2(p1+p2=1)p_2(p_1 + p_2 = 1)
f1(y)f_1(\mathbf{y})和f2(y)f_2(\mathbf{y})分别是总体G1G_1和G2G_2中y\mathbf{y}的概率密度函数

记号：

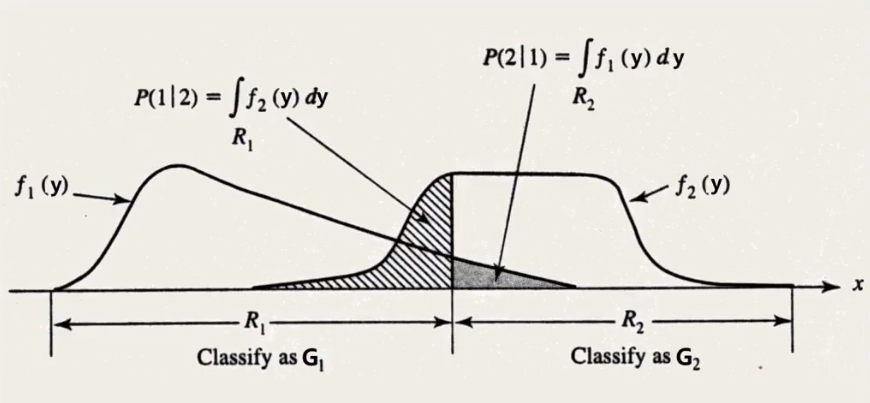
  • R1R_1和R2R_2代表分类规则给出的分类区域，如果新观测对象属于RkR_k，我们说该对象来自Gk,k=1,2G_k, k =1,2，R1,R2R_1,R_2是整个空间的分割
  • P(1∣2)P(1|2)是我们将对象y\mathbf{y}分为G1(y∈R1)G_1(\mathbf{y} \in R_1)然而实际上它来自G2G_2的误判条件概率

P(1∣2)=P(y∈R1∣G2)=∫R1f2(y)dyP(2∣1)=P(y∈R2∣G1)=∫R2=Ω−R1f1(y)dy=1−∫R1f1(y)dy\begin{aligned} P(1|2) &= P(\mathbf{y} \in R_1|G_2) = \int_{R_1}f_2(\mathbf{y})\mathrm{d}\mathbf{y} \\ P(2|1) &= P(\mathbf{y} \in R_2|G_1) = \int_{R_2=\Omega - R_1}f_1(\mathbf{y})\mathrm{d}\mathbf{y} = 1 - \int_{R_1}f_1(\mathbf{y})\mathrm{d}\mathbf{y} \end{aligned}

错分率

P(观测对象被错分到G1)=P(y∈R1∣G2)P(G2)=P(1∣2)p2P(观测对象被错分到G2)=P(y∈R2∣G1)P(G1)=P(2∣1)p1\begin{aligned} P(\text{观测对象被错分到}G_1) &= P(\mathbf{y} \in R_1|G_2)P(G_2) = P(1|2)p_2 \\ P(\text{观测对象被错分到}G_2) &= P(\mathbf{y} \in R_2|G_1)P(G_1) = P(2|1)p_1 \end{aligned}

错分成本

记c(1∣2)c(1|2)为错误地将来自总体G2G_2的观测对象y\mathbf{y}错分到G1G_1的代价/成本，类似可定义c(2∣1)c(2|1)

G1G1 G2G2
G1G1 00 c(2∣1)c(2\vert 1)
G2G2 c(1∣2)c(1\vert 2) 00

贝叶斯分类法则目标是最小化错分的期望误判代价

ECM=c(2∣1)P(2∣1)p1+c(1∣2)P(1∣2)p2=c(2∣1)p1{1−∫R1f1(y)dy}+c(1∣2)p2∫R1f2(y)dy∝∫R1{f2(y)c(1∣2)p2−f1(y)c(2∣1)p1}d(y)\begin{aligned} \text{ECM} &= c(2|1)P(2|1)p_1 + c(1|2)P(1|2)p_2 \\ &= c(2|1)p_1\lbrace 1 - \int_{R_1}f_1(\mathbf{y})\mathrm{d}\mathbf{y} \rbrace + c(1|2)p_2 \int_{R_1}f_2(\mathbf{y})\mathrm{d}\mathbf{y} \\ &\propto \int_{R_1} \lbrace f_2(\mathbf{y})c(1|2)p_2 - f_1(\mathbf{y})c(2|1)p_1 \rbrace \mathrm{d}(\mathbf{y}) \end{aligned}

求得一个积分区域，要使积分下的有向面积最小，即R1R_1包含积分项函数小于0的那些y\mathbf{y}
基于最小化ECM的思想

R1:f1(y)f2(y)≥c(1∣2)c(2∣1)p2p1R2:f2(y)f1(y)≥c(2∣1)c(1∣2)p1p2\begin{aligned} R_1: \frac{f_1(\mathbf{y})}{f_2(\mathbf{y})} \geq \frac{c(1|2)}{c(2|1)}\frac{p_2}{p_1} \\ R_2: \frac{f_2(\mathbf{y})}{f_1(\mathbf{y})} \geq \frac{c(2|1)}{c(1|2)}\frac{p_1}{p_2} \end{aligned}

特殊形式：p2p1=1\frac{p_2}{p_1} = 1（先验概率相同）

R1:f1(y)f2(y)≥c(1∣2)c(2∣1)R2:f2(y)f1(y)<c(1∣2)c(2∣1)\begin{aligned} R_1: \frac{f_1(\mathbf{y})}{f_2(\mathbf{y})} \geq \frac{c(1|2)}{c(2|1)} \\ R_2: \frac{f_2(\mathbf{y})}{f_1(\mathbf{y})} < \frac{c(1|2)}{c(2|1)} \end{aligned}

特殊形式：c(1∣2)c(2∣1)=1\frac{c(1|2)}{c(2|1)} = 1（错分成本相同）

R1:f1(y)f2(y)≥p2p1R2:f2(y)f1(y)<p2p1\begin{aligned} R_1: \frac{f_1(\mathbf{y})}{f_2(\mathbf{y})} \geq \frac{p_2}{p_1} \\ R_2: \frac{f_2(\mathbf{y})}{f_1(\mathbf{y})} < \frac{p_2}{p_1} \end{aligned}

特殊形式：p2p1=c(1∣2)c(2∣1)=1\frac{p_2}{p_1} = \frac{c(1|2)}{c(2|1)} = 1

R1:f1(y)f2(y)≥1R2:f2(y)f1(y)<1\begin{aligned} R_1: \frac{f_1(\mathbf{y})}{f_2(\mathbf{y})} \geq 1 \\ R_2: \frac{f_2(\mathbf{y})}{f_1(\mathbf{y})} < 1 \end{aligned}

当两群体来自具有相同协方差矩阵的正态分布Np(μ1,Σ)N_p(\mathbf{\mu}_1, \Sigma)和Np(μ2,Σ)N_p(\mathbf{\mu}_2, \Sigma)时，贝叶斯法则可表示为

(y‾1−y‾2)TS(pl)−1y0−12(y‾1−y‾2)TS(pl)−1(y‾1+y‾2)≥∈[c(1∣2)c(2∣1)p2p1](\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2)^TS_(pl)^{-1}\mathbf{y}_0 - \frac{1}{2}(\overline{\mathbf{y}}_1 - \overline{\mathbf{y}}_2)^TS_(pl)^{-1}(\overline{\mathbf{y}}_1 + \overline{\mathbf{y}}_2) \geq \in \left[ \frac{c(1|2)}{c(2|1)}\frac{p_2}{p_1} \right]

当两群体具有相同协方差矩阵的正态分布时，贝叶斯法则的特殊情形等价于Fisher’s LDA分类法则

多群体Fisher分类

假设协方差矩阵相同，Fisher分类法则旨在比较新观测对象y0\mathbf{y}_0和均值y‾k,k=1,2,⋯ ,g\overline{\mathbf{y}}_k, k = 1, 2, \cdots, g之间的马氏距离

(y0−y‾k)TSpl−1(y0−y‾k)(\mathbf{y}_0 - \overline{\mathbf{y}}_k)^TS^{-1}_{pl}(\mathbf{y}_0 - \overline{\mathbf{y}}_k)

并将其分到有最小距离的群体

多群体贝叶斯分类

多群体的误判代价较为复杂，因为要考虑g(g−1)g(g - 1)组代价，因此我们假设相同的误判代价，即

R1:f1(y)f2(y)≥c(1∣2)c(2∣1)R2:f2(y)f1(y)<c(1∣2)c(2∣1)\begin{aligned} R_1: \frac{f_1(\mathbf{y})}{f_2(\mathbf{y})} \geq \frac{c(1|2)}{c(2|1)} \\ R_2: \frac{f_2(\mathbf{y})}{f_1(\mathbf{y})} < \frac{c(1|2)}{c(2|1)} \end{aligned}

将y0\mathbf{y}_0分到pkfk(y0)p_kf_k(\mathbf{y}_0)最大的那个组

  • pkp_k：先验概率
  • fk(y0)f_k(\mathbf{y}_0)：密度函数

主成分分析

降维：用少数几个新的变量代替原有变量，合并重复信息，但不损失重要信息
主成分分析：在所有可能的Y1,Y2,⋯ ,YpY_1, Y_2, \cdots, Y_p的线性组合模式中，寻找一个或几个可以最大程度区分数据的线性组合/加权平均

  • LDA：线性判别分析寻求最大化两个或多个群体之间距离的线性组合
  • PCA：主成分分析只有一个群体，找到能使这个群体中个体之间分的最开的变量组合

总体主成分推导

            graph LR
            原式变量--总体PCA-->主成分
  • 线性组合
  • 信息不重合
    • 相关系数为0
  • 按重要性排序
    • var(Z1),var(Z2),⋯ ,var(Zp)var(Z_1), var(Z_2), \cdots, var(Z_p)

记原式变量y=(Y1,Y2,⋯ ,Yp)T\mathbf{y} = (Y_1, Y_2, \cdots, Y_p)^T，其协方差矩阵为Σ\Sigma
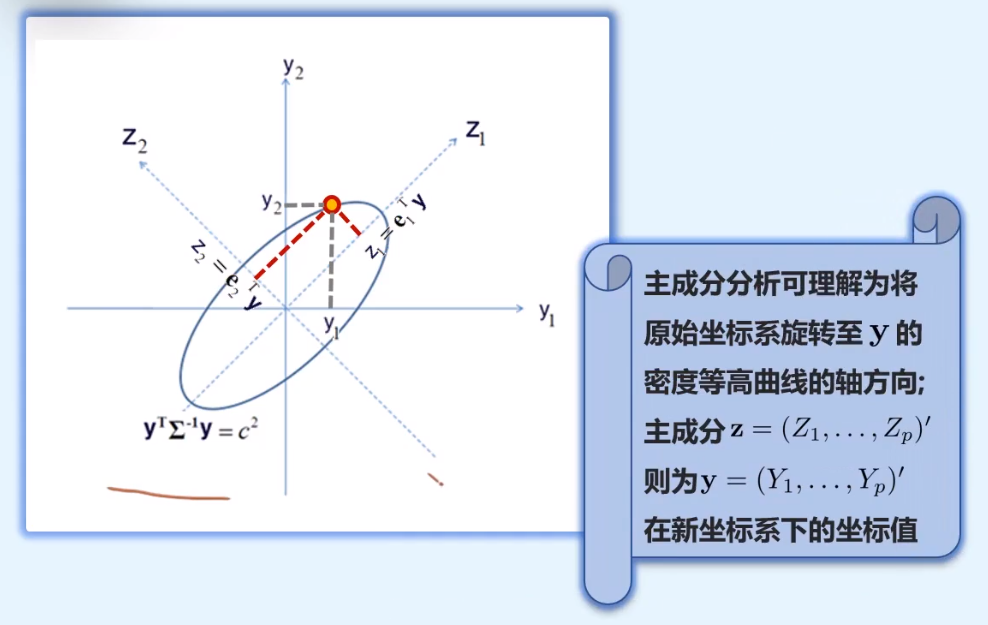
主成分分析试图定义一组互不相关的变量，称为Y1,Y2,⋯ ,YpY_1, Y_2, \cdots, Y_p的主成分，记为Z1,Z2,⋯ ,ZpZ_1, Z_2, \cdots, Z_p，每一个主成分都是Y1,Y2,⋯ ,YpY_1, Y_2, \cdots, Y_p的线性组合

Z1=a1Ty=a11Y1+a12Y2+⋯+a1pYpZ2=a2Ty=a21Y1+a22Y2+⋯+a2pYp⋮Zp=apTy=ap1Y1+ap2Y2+⋯+appYp\begin{aligned} Z_1 &= \mathbf{a}^T_1\mathbf{y} = a_{11}Y_1 + a_{12}Y_2 + \cdots + a_{1p}Y_p \\ Z_2 &= \mathbf{a}^T_2\mathbf{y} = a_{21}Y_1 + a_{22}Y_2 + \cdots + a_{2p}Y_p \\ \vdots \\ Z_p &= \mathbf{a}^T_p\mathbf{y} = a_{p1}Y_1 + a_{p2}Y_2 + \cdots + a_{pp}Y_p \end{aligned}

则方差和协方差为

var(Zj)=var(ajTy)=aTΣajCov(Zj,Zk)=aTΣak\begin{aligned} var(Z_j) &= var(\mathbf{a}^T_j\mathbf{y}) \\ &= \mathbf{a}^T\Sigma\mathbf{a}_j \\ \\ Cov(Z_j ,Z_k) &= \mathbf{a}^T\Sigma\mathbf{a}_k \end{aligned}

实际为求解a1,a2,⋯ ,apa_1, a_2, \cdots, a_p使var(Zj)var(Z_j)最大，Cov(Zj,Zk)Cov(Z_j ,Z_k)为0

主成分Z1,Z2,⋯ ,ZpZ_1, Z_2, \cdots, Z_p按照方差贡献度依次导出

  • 第一主成分Z1=a1TyZ_1 = \mathbf{a}^T_1\mathbf{y}在满足a1Ta1=1\mathbf{a}^T_1\mathbf{a}_1 = 1时（标准向量），最大化方差a1TΣa1\mathbf{a}^T_1\Sigma\mathbf{a}_1

max⁡a1≠0a1TΣa1a1Ta1\underset{\mathbf{a}_1 \neq 0}{\max}\frac{\mathbf{a}^T_1\Sigma\mathbf{a}_1}{\mathbf{a}^T_1\mathbf{a}_1}

  • 第二主成分Z2=a2TyZ_2 = \mathbf{a}^T_2\mathbf{y}在满足a2Ta2=1\mathbf{a}^T_2\mathbf{a}_2 = 1时且a2TΣa1=0\mathbf{a}^T_2\Sigma\mathbf{a}_1 = 0（信息不重合），最大化方差a2TΣa2\mathbf{a}^T_2\Sigma\mathbf{a}_2

max⁡a2≠0, a2TΣa1=0a2TΣa2a2Ta2\underset{\mathbf{a}_2 \neq 0,\ \mathbf{a}^T_2\Sigma\mathbf{a}_1 = 0}{\max}\frac{\mathbf{a}^T_2\Sigma\mathbf{a}_2}{\mathbf{a}^T_2\mathbf{a}_2}

  • 第jj主成分Zj=ajTyZ_j = \mathbf{a}^T_j\mathbf{y}在满足ajTaj=1\mathbf{a}^T_j\mathbf{a}_j = 1时且ajTΣak=0(k=1,2,⋯ ,j−1)\mathbf{a}^T_j\Sigma\mathbf{a}_k = 0(k=1, 2, \cdots, j-1)（信息不重合），最大化方差ajTΣaj\mathbf{a}^T_j\Sigma\mathbf{a}_j

max⁡a2≠0, ajTΣak=0a2TΣa2a2Ta2\underset{\mathbf{a}_2 \neq 0,\ \mathbf{a}^T_j\Sigma\mathbf{a}_k = 0}{\max}\frac{\mathbf{a}^T_2\Sigma\mathbf{a}_2}{\mathbf{a}^T_2\mathbf{a}_2}

  • 第pp主成分Zj=ajTyZ_j = \mathbf{a}^T_j\mathbf{y}在满足apTap=1\mathbf{a}^T_p\mathbf{a}_p = 1时，最小化方差ajTΣaj\mathbf{a}^T_j\Sigma\mathbf{a}_j

min⁡ap≠0apTΣapapTap\underset{\mathbf{a}_p \neq 0}{\min}\frac{\mathbf{a}^T_p\Sigma\mathbf{a}_p}{\mathbf{a}^T_p\mathbf{a}_p}

见[线性代数] - Courant Fischer定理

记(λ1,e1),⋯ ,(λp,ep)(\lambda_1, \mathbf{e}_1), \cdots, (\lambda_p, \mathbf{e}_p)为协方差矩阵Σ\Sigma的特征值-特征向量，λ1≥λ2≥⋯≥λn≥0\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_n \geq 0，并且特征向量为标准化特征向量，则变量Y1,Y2,⋯ ,YpY_1, Y_2, \cdots, Y_p的第jj个主成分由下式给出

Zj=ejTy=ej1Y1+ej2Y2+⋯+ejpYn,j=1,2,⋯ ,pZ_j = \mathbf{e}^T_j\mathbf{y} = e_{j1}Y_1 + e_{j2}Y_2 + \cdots + e_{jp}Y_n, \quad j = 1, 2, \cdots, p

  • 这里有var(Zj)=ejTΣej=λjvar(Z_j) = \mathbf{e}^T_j\Sigma\mathbf{e}_j = \lambda_j
  • 并且有Cov(Zj,Zk)=ejTΣek=0Cov(Z_j, Z_k) = \mathbf{e}^T_j\Sigma\mathbf{e}_k = 0
  • 进一步，还有

∑j=1pvar(Zj)=∑j=1pvar(Yj)\sum^p_{j=1}var(Z_j) = \sum^p_{j=1}var(Y_j)

第kk个主成分贡献的方差，占总体方差的比例可表示如下

λk∑j=1pλj,k=1,2,⋯ ,p\frac{\lambda_k}{\sum^p_{j=1}\lambda_j}, \quad k = 1, 2, \cdots, p

如果前几个主成分贡献大部分方差/信息(如80%)，那么这些主成分能够以较少的信息损失来综合原始变量的信息，构成几个综合指标

总体主成分分析

如果变量y=(Y1,Y2,⋯ ,Yp)T\mathbf{y} = (Y_1, Y_2, \cdots, Y_p)^T的波动性（由于度量单位不同等原因）差距过大，直接由协方差矩阵Σ\Sigma生成的主成分会由方差大的变量主导，这时我们可对每个变量分别进行标准化

Wj=Yj−μjσjj⇓w=(W1,W2,⋯ ,Wp)T=DS−1(y−μ)Ds=diag(σ11,⋯ ,σpp)\begin{gathered} W_j = \frac{Y_j - \mu_j}{\sqrt{\sigma_{jj}}} \\ \Downarrow \\ \mathbf{w} = (W_1, W_2, \cdots, W_p)^T = D^{-1}_S(\mathbf{y} - \mathbf{\mu}) \quad D_s = diag(\sqrt{\sigma_{11},\cdots,\sigma_{pp}}) \end{gathered}

Cov(w)=Ds−1ΣDs−1=ρCov(\mathbf{w}) = D^{-1}_s\Sigma D^{-1}_s = \rho，对w\mathbf{w}做主成分分析就是在对y\mathbf{y}的相关系数矩阵做特征值和特征向量的分解（主成分分析）

记(λ1~,e1~),⋯ ,(λp~,ep~)(\tilde{\lambda_1}, \tilde{\mathbf{e}_1}), \cdots, (\tilde{\lambda_p}, \tilde{\mathbf{e}_p})为y\mathbf{y}的相关系数矩阵PP的特征值-特征向量，λ1~≥λ2~≥⋯≥λn~≥0\tilde{\lambda_1} \geq \tilde{\lambda_2} \geq \cdots \geq \tilde{\lambda_n} \geq 0，并且特征向量为标准化特征向量，则y\mathbf{y}基于PP的主成分分析等价于W1,W2,⋯ ,WspW_1, W_2, \cdots, Ws_p的第jj个主成分由下式给出

Vj=e~jTw=e~j1W1+e~j2W2+⋯+e~jpWp,j=1,⋯ ,pV_j = \tilde{\mathbf{e}}^T_j\mathbf{w} = \tilde{e}_{j1}W_1 + \tilde{e}_{j2}W_2 + \cdots + \tilde{e}_{jp}W_p, \quad j=1,\cdots,p

同时，我们也有

∑j=1pvar(Vj)=∑j=1pvar(Wj)=ρ\sum^p_{j=1}var(V_j) = \sum^p_{j=1}var(W_j) = \rho

  • 基于相关系数矩阵PP的主成分分析不受度量单位影响
  • PP与Σ\Sigma的特征值、特征向量不同，因此两组主成分的数值和方向均不同，一组主成分并不是另一组主成分的简单变换
  • 如果变量数值差异很大，推荐进行标准化来获得一个较平衡的数据集

样本主成分分析

            graph LR
            原式数据矩阵--样本PCA-->主成分数据矩阵

样本主成分推导

y1,y2,⋯ ,yn\mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n表示nn个pp维随机样本，

  • yi=(yi1,yi2,⋯ ,yip)T\mathbf{y}_i = (y_{i1}, y_{i2}, \cdots, y_{ip})^T
  • 样本均值向量：y‾\overline{\mathbf{y}}
  • 样本协方差矩阵：SS
  • 样本相关系数矩阵：RR

记(λ1^,e1^),⋯ ,(λp^,ep^)(\hat{\lambda_1}, \hat{\mathbf{e}_1}), \cdots, (\hat{\lambda_p}, \hat{\mathbf{e}_p})为SS的相关系数矩阵PP的特征值-特征向量，则第ii个样本得到的第jj个主成分为

zij=e^jTyi=e^j1yi1+e^j2yi2+⋯+e^jpyip,j=1,2,⋯ ,pi=1,2,⋯ ,nz_{ij} = \hat{\mathbf{e}}^T_j\mathbf{y}_i = \hat{e}_{j1}y_{i1} + \hat{e}_{j2}y_{i2} + \cdots + \hat{e}_{jp}y_{ip}, \quad j=1, 2, \cdots, p\quad i = 1, 2, \cdots, n

  • szj2=e^jTSe^j=λ^js^2_{zj} = \hat{\mathbf{e}}^T_jS\hat{\mathbf{e}}_j = \hat{\lambda}_j
  • szjzk=e^jTSe^k=0s_{z_jz_k} = \hat{\mathbf{e}}^T_jS\hat{\mathbf{e}}_k = 0
  • j,k=1,2,⋯ ,p,j≠kj,k = 1, 2, \cdots, p, j \neq k

记sjjs_{jj}为SS的第jj个对角元，那么有

样本总方差=∑j=1psjj=∑j=1pλ^j\text{样本总方差} = \sum^p_{j=1}s_{jj} = \sum^p_{j=1}\hat{\lambda}_j

总体主成分分析中，利用相关系数矩阵构造主成分的结论可以类似地推广到样本主成分分析

经过中心化的一系列主成分

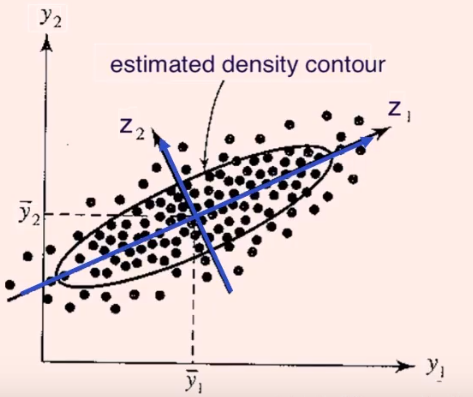
zij=e^jT(yi−y‾),j=1,2,⋯ ,p,i=1,2,⋯ ,nz_{ij} = \hat{\mathbf{e}}^T_j(\mathbf{y}_i - \overline{\mathbf{y}}), \quad j = 1, 2, \cdots, p, i = 1, 2, \cdots, n

看作原理坐标系的原点平移到y‾\overline{\mathbf{y}}，然后旋转坐标轴，使得坐标轴与数据最大方差方向一致

样本主成分个数的选择

  • 百分比截点法：使用一定数目的主成分来反映足够比例（80%）的总方差

∑j=1kλj∑j=1pλj\frac{\sum^k_{j=1}\lambda_j}{\sum^p_{j=1}\lambda_j}

  • 平均截点：使用特征值大于平均特征值∑j=1pλ1/p\sum^p_{j=1}\lambda_1/p的主成分
    • 被广泛使用
    • 当数据能够相对较小的维度下被很好地归纳时，特征值可以明显地分为“大特征值”和“小特征值”
  • 碎石图：画出λj\lambda_j关于jj的散点图，从图上寻找能区分“大特征值”和“小特征值”的分界点

因子分析

对于pp个原始变量Y1,Y2,⋯ ,YpY_1, Y_2, \cdots, Y_p来说，那些高度相关的变量很可能会遵循一个共同的潜在结构，称为公共因子
公共因子通常无法观测，故称为潜变量

因子分析旨在提出因子模型，来研究如何让用几个公共因子，记作F1,F2,⋯ ,FmF_1, F_2, \cdots, F_m，通常m<pm < p来刻画原始变量之间的相关性

因子分析 主成分分析
通常指是一种模型 不涉及模型
通过公共因子解释原始变量间的相关性 通过综合指标解释个体之间的差异性
原变量为因子的线性组合 主成分为原变量的线性组合
结果不唯一 结果唯一

单因子模型

Yj=ljF+εjY_j =l_jF + \varepsilon_j

  • 公共因子：FF
  • 特殊因子：εj\varepsilon_j
  • 系数/载荷：ljl_j

大多数时候需要多个因子来刻画：正交因子模型

正交因子模型

记随机向量y=(Y1,Y2,⋯ ,Yp)T\mathbf{y} = (Y_1, Y_2, \cdots, Y_p)^T的均值为μ\mathbf{\mu}，协方差矩阵为Σ\Sigma，正交因子模型假定y\mathbf{y}线性依赖于mm个不可观测公共因子f=(F1,F2,⋯ ,Fm)T\mathbf{f} = (F_1, F_2, \cdots, F_m)^T和pp个不可观测的特殊因子ε=(ε1,ε2,⋯ ,εp)T\mathbf{\varepsilon} = (\varepsilon_1, \varepsilon_2, \cdots, \varepsilon_p)^T，通常m<pm < p

Y1−μ1=l11F1+l12F2+⋯+l1mFm+ε1Y2−μ2=l21F1+l22F2+⋯+l2mFm+ε2⋮Yp−μp=lp1F1+lp2F2+⋯+lpmFm+εp\begin{aligned} Y_1 - \mu_1 = l_{11}F_1 + l_{12}F_2 + \cdots + l_{1m}F_m + \varepsilon_1 \\ Y_2 - \mu_2 = l_{21}F_1 + l_{22}F_2 + \cdots + l_{2m}F_m + \varepsilon_2 \\ \vdots \\ Y_p - \mu_p = l_{p1}F_1 + l_{p2}F_2 + \cdots + l_{pm}F_m + \varepsilon_p \end{aligned}

系数ljkl_{jk}称为第jj个变量在第kk个因子上的载荷，体现了该因子对此变量的解释力

yp×1−up×1=Lp×mfm×1+εp×1\mathbf{y}_{p\times 1} - \mathbf{u}_{p\times 1} = L_{p\times m}\mathbf{f}_{m\times 1} + \varepsilon_{p\times 1}

  • LL：载荷矩阵

其中f\mathbf{f}和ε\varepsilon假设满足

  • 假设f\mathbf{f}是正交的：不相关
    • 若2个公共因子有很强相关性，那么就可以合并为一个公共因子
  • 假设ε\mathbf{\varepsilon}的都是互不相关的
  • 同时f\mathbf{f}和ε\mathbf{\varepsilon}是无关的

{E(f)=0m×1Cov(f)=E(ffT)=I(m×m)E(ε)=0p×1Cov(ε)=E(εεT)=Ψp×p=[ψ10⋯00ψ2⋯0⋮⋮⋱⋮00⋯ψp]Cov(ε,f)=0p×m\begin{cases} E(\mathbf{f}) &= \mathbf{0}_{m\times 1} \\ Cov(\mathbf{f}) &= E(\mathbf{f}\mathbf{f}^T) = I_(m\times m) \\ \\ E(\mathbf{\varepsilon}) &= \mathbf{0}_{p\times 1} \\ Cov(\varepsilon) &= E(\varepsilon\varepsilon^T) = \Psi_{p\times p} = \begin{bmatrix} \psi_1 & 0 & \cdots & 0 \\ 0 & \psi_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \psi_p \end{bmatrix} \\ Cov(\mathbf{\varepsilon}, \mathbf{f}) &= \mathbf{0}_{p\times m} \end{cases}

  • 矩阵形式模型：y−u=Lf+ε\mathbf{y} - \mathbf{u} = L\mathbf{f} + \mathbf{\varepsilon}
  • 元素形式模型：Yj−μj=lj1F1+lj2F2+ljmFm+εj,j=1,⋯ ,pY_j - \mu_j = l_{j1}F_1 + l_{j2}F_2 + l_{jm}F_m + \varepsilon_j, j = 1,\cdots,p

Cov(y,f)=Cov(Lf+ε,f)=L\begin{aligned} Cov(\mathbf{y}, \mathbf{f}) &= Cov(L\mathbf{f} + \mathbf{\varepsilon}, \mathbf{f}) \\ &= L \end{aligned}

因此载荷ljkl_{jk}测度了第jj个变量与第kk个公共因子之间的关联Cov(Yj,Fk)=ljkCov(Y_j, F_k) = l_{jk}

Σ=Cov(y)=LLT+Ψσ=var(Yj)=hj2+ψj,hj2=lj12+lj22+⋯+ljm2\begin{aligned} \Sigma &= Cov(\mathbf{y}) = LL^T + \Psi \\ \sigma &= var(Y_j) = h^2_j + \psi_j,\quad h^2_j = l^2_{j1} + l^2_{j2} + \cdots + l^2_{jm} \end{aligned}

  • hj2h^2_j体现了共同性，指由mm个公共因子贡献的方差
  • ψj\psi_j称为唯一性或个体方差，指无法由公共因子贡献的方差部分
  • σjjT=Cov(Yj,YjT)=lj1lj′1+⋯+ljmlj′m,j≠j′\sigma_{jj}^T = Cov(Y_j,Y_j^T) = l_{j1}l_{j'1} + \cdots + l_{jm}l_{j'm}, j \neq j'

载荷估计方法

主成分法

y−u=Lf+ε\mathbf{y} - \mathbf{u} = L\mathbf{f} + \mathbf{\varepsilon}

通过因子模型的协方差矩阵分解

Σ=Lp×mLp×mT+Ψ\Sigma = L_{p\times m} L^T_{p\times m} + \Psi

利用谱分解

Σ=∑j=1pλjejejT=Λp×pΛp×pTΛ=(λ1e1,⋯ ,λpep)\Sigma = \sum^p_{j=1}\lambda_je_je^T_j = \Lambda_{p\times p} \Lambda^T_{p\times p} \quad \Lambda = (\sqrt{\lambda_1}\mathbf{e}_1, \cdots, \sqrt{\lambda_p}\mathbf{e}_p)

当最后p−mp - m个特征值很小的时候，我们可定义

L=(λ1e1,⋯ ,λpep)L = (\sqrt{\lambda_1}\mathbf{e}_1, \cdots, \sqrt{\lambda_p}\mathbf{e}_p)

则Σ=LLT\Sigma = LL^T，而Ψ\Psi可以补全Σ\Sigma的对角线部分

Ψ=diag(ψ1,⋯ ,ψp),ψj=σjj−∑k=1mljk2,j=1,⋯ ,p\Psi = diag(\psi_1, \cdots, \psi_p), \quad \psi_j = \sigma_{jj} - \sum^m_{k=1}l^2_{jk}, j =1,\cdots,p

定理：(λ^j,e^j),j=1,2,⋯ ,p(\hat{\lambda}_j, \hat{\mathbf{e}}_j), j=1, 2, \cdots, p为样本协方差矩阵SS的排序后标准化特征对，记m<pm < p为公共因子的数目，那么因子载荷矩阵估计的主成分分解为

L^=(λ^1e^1λ^2e^2⋯λ^me^m)\hat{L} = \begin{pmatrix} \sqrt{\hat{\lambda}_1}\hat{\mathbf{e}}_1 & \sqrt{\hat{\lambda}_2}\hat{\mathbf{e}}_2 &\cdots & \sqrt{\hat{\lambda}_m}\hat{\mathbf{e}}_m \end{pmatrix}

个体方差的估计为S−L^L^TS - \hat{L}\hat{L}^T的对角元素，即Ψ^=diag(ψ^1,ψ^2,⋯ ,ψ^p)\hat{\Psi} = diag(\hat{\psi}_1, \hat{\psi}_2, \cdots, \hat{\psi}_p)

  • ψ^j=sjj−∑k=1ml^jk2\hat{\psi}_j = s_{jj} - \sum^m_{k=1}\hat{l}^2_{jk}
  • 共同度：h^j2=l^j12+⋯+l^jm2\hat{h}^2_j = \hat{l}^2_{j1} + \cdots + \hat{l}^2_{jm}

第kk个因子的载荷估计与第kk个主成分的系数成比例

S的对焦元素等于L^L^T+Ψ^\hat{L}\hat{L}^T + \hat{\Psi}的对角元素，然而，S的非对角元素通常不能由L^L^T+Ψ^\hat{L}\hat{L}^T + \hat{\Psi}完全复原

第kk个因子对总方差s11+s22+⋯+spp=tr(S)s_{11} + s_{22} + \cdots + s_{pp} = tr(S)的贡献为

∑j=1pl^jk2=λ^k\sum^p_{j=1}\hat{l}^2_{jk} = \hat{\lambda}_k

贡献比例

λ^ktr(S),k=1,2,⋯ ,m\frac{\hat{\lambda}_k}{tr(S)}, \quad k =1, 2, \cdots, m

类似主成分分析，当变量的度量单位/量纲相差很多时，建议使用标准化后的变量进行因子分析，这等价于基于样本相关系数矩阵RR使用主成分法，即将SS换成RR

确定mm：参考主成分分析，评估被忽略的特征值的贡献，即可以使用百分比截点，平均截点和碎石图
还可以使用相关系数矩阵，把高度相关的变量分为一组为一个公共因子

主因子法

主成分方法中，忽略了Ψ\Psi，而主因子法。主轴法，则使用一个初始的估计值，从而对S−Ψ^(0)S - \hat{\Psi}^{(0)}或R−Ψ^(0)R - \hat{\Psi}^{(0)}使用与主成分方法相同的操作进行因子分析

我们可以迭代的更新估计值Ψ^(0)\hat{\Psi}^{(0)}以及S−Ψ^(0)S - \hat{\Psi}^{(0)}或R−Ψ^(0)R - \hat{\Psi}^{(0)}的分解直到收敛

因为S−Ψ^(0)S - \hat{\Psi}^{(0)}或R−Ψ^(0)R - \hat{\Psi}^{(0)}可能不是正定的，这个方法有可能得到负的特征值，使结果较难解释

极大似然法

当样本f1,f2,⋯ ,fn\mathbf{f}_1, \mathbf{f}_2, \cdots, \mathbf{f}_n和ε1,ε2,⋯ ,εn\mathbf{\varepsilon}_1, \mathbf{\varepsilon}_2, \cdots, \mathbf{\varepsilon}_n服从联合正态分布，y1,y2,⋯ ,yn\mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n也因此独立同分布的服从Np(μ,Σ)N_p(\mathbf{\mu}, \Sigma)分布时（Σ=LLT+Ψ\Sigma = LL^T + \Psi），Σ\Sigma的似然函数可以如下表示

L(Σ)∝∣Σ∣−n2exp⁡[−12tr{Σ−1(∑i=1n(yi−y‾)(yi−y‾)T)}]L(\Sigma) \propto |\Sigma|^{-\frac{n}{2}} \exp\left[ -\frac{1}{2}tr \left\lbrace \Sigma^{-1}(\sum^n_{i=1}(\mathbf{y}_i - \overline{\mathbf{y}})(\mathbf{y}_i - \overline{\mathbf{y}})^T) \right\rbrace \right]

其中μ^MLE=y‾\hat{\mathbf{\mu}}_{MLE} = \overline{\mathbf{y}}已经带入上式，那么LL和Ψ\Psi的极大似然估计可以通过迭代计算得到

估计因子得分

有时希望得到因子得分，f^i=(F^i1,F^i2,⋯ ,F^im),i=1,2,⋯ ,n\hat{\mathbf{f}}_i = (\hat{F}_{i1}, \hat{F}_{i2}, \cdots, \hat{F}_{im}),i = 1, 2, \cdots, n，即每个因子在不同个体上的取值，从而可以：查看不同个体的因子表现情况

  • 因子模型：yi−u=Lfi+εi\mathbf{y}_i - \mathbf{u} = L\mathbf{f}_i + \mathbf{\varepsilon}_i
  • 回归模型：y=Xβ+ε\mathbf{y} = X\mathbf{\beta} + \mathbf{\varepsilon}
    • β^=(XTX)−1XTy\hat{\beta} = (X^TX)^{-1}X^T\mathbf{y}

由于ε\varepsilon的方差不相同，我们可以通过加权最小二乘法来估计f\mathbf{f}：

f=(LTΨ−1L)−1LTΨ−1(y−μ)\mathbf{f} = (L^T\Psi^{-1}L)^{-1}L^T\Psi^{-1}(\mathbf{y} - \mathbf{\mu})

将已估计的参数L^,Ψ^\hat{L}, \hat{\Psi}和μ^=y‾\hat{\mu} = \overline{\mathbf{y}}代入上式：

f^i=(L^TΨ^−1L^)−1L^TΨ^−1(yi−μ),i=1,2,⋯ ,n\hat{\mathbf{f}}_i = (\hat{L}^T\hat{\Psi}^{-1}\hat{L})^{-1}\hat{L}^T\hat{\Psi}^{-1}(\mathbf{y}_i - \mathbf{\mu}), \quad i = 1, 2, \cdots, n

回归法：基于正态假设

(y−μf)∼Np+m(0[Σ=LLT+ΨLLTI])\begin{pmatrix} \mathbf{y} - \mathbf{\mu} \\ \mathbf{f} \end{pmatrix} \sim N_{p+m}\begin{pmatrix} \mathbf{0} & \begin{bmatrix} \Sigma = LL^T + \Psi & L \\ L^T & I \end{bmatrix} \end{pmatrix}

则f\mathbf{f}在给定y\mathbf{y}时的条件分布为正态分布，均值为

E(f∣y)=LTΣ−1(y−μ)E(\mathbf{f}|\mathbf{y}) = L^T\Sigma^{-1}(\mathbf{y} - \mathbf{\mu})

就可以得到第ii个因子得分的估计

f^i=L^T(L^L^T+Ψ^)−1(yi−y‾)orf^i=L^TS−1(yi−y‾)\hat{\mathbf{f}}_i = \hat{L}^T(\hat{L}\hat{L}^T + \hat{\Psi})^{-1}(\mathbf{y}_i - \overline{\mathbf{y}}) \quad or \quad \hat{\mathbf{f}}_i = \hat{L}^TS^{-1}(\mathbf{y}_i - \overline{\mathbf{y}})

因子旋转

y−u=Lf+ε\mathbf{y} - \mathbf{u} = L\mathbf{f} + \mathbf{\varepsilon}

以上因子模型等价于y−u=L∗f∗+ε\mathbf{y} - \mathbf{u} = L^*\mathbf{f}^* + \mathbf{\varepsilon}

  • L∗=LTL^* = LT
  • f∗=TTf\mathbf{f}^* = T^T\mathbf{f}
  • T→TTT=TTT=IT \rightarrow TT^{T} = T^TT = I

所以因子及其载荷矩阵并不唯一，可按照任意正交矩阵TT提供的方向旋转，寻找使因子及载荷结构更简单，解释更清晰的旋转方向TT

Y1−μ1=l11F1+l12F2+⋯+l1mFm+ε1Y2−μ2=l21F1+l22F2+⋯+l2mFm+ε2⋮Yp−μp=lp1F1+lp2F2+⋯+lpmFm+εp\begin{aligned} Y_1 - \mu_1 = l_{11}F_1 + l_{12}F_2 + \cdots + l_{1m}F_m + \varepsilon_1 \\ Y_2 - \mu_2 = l_{21}F_1 + l_{22}F_2 + \cdots + l_{2m}F_m + \varepsilon_2 \\ \vdots \\ Y_p - \mu_p = l_{p1}F_1 + l_{p2}F_2 + \cdots + l_{pm}F_m + \varepsilon_p \end{aligned}

  • 载荷矩阵LL代表原始变量和公共因子之间的关系
  • 我们希望每个原始变量都由某个因子主要决定
    • 对应载荷数值很大
    • 对应其他因子关系不大，载荷数值很小

几何的角度，L^\hat{L}的第jj行的载荷构成了原始变量YjY_j在因子/载荷空间的坐标

因子旋转的目标：让坐标轴靠近尽可能多的点（=0=0）

正交旋转

  • 原来垂直的坐标轴经过旋转后仍保持垂直
  • 角度和距离都保持不变
  • 共同度不变
  • 点的相对位置也维持原则
  • 只有参考系改变了

我们选择一个角度ϕ\phi来让坐标轴更加靠近点构成的聚类，新的选择载荷(l^j1∗,l^j2∗)(\hat{l}^*_{j1}, \hat{l}^*_{j2})可以通过图像测量出来，或者通过L^∗=LT\hat{L}^* = LT得到，其中

T=(cos⁡ϕ−sin⁡ϕsin⁡ϕcos⁡ϕ)T = \begin{pmatrix} \cos\phi & -\sin\phi \\ \sin \phi & \cos\phi \end{pmatrix}

对于维度大于2的情况，最常用的为最大方差法，也就是寻找能够最大化载荷矩阵中每一列载荷平方的方差的选择载荷

斜交旋转

  • 不要求轴保持垂直
  • 旋转更加自由
  • 让更多的点靠近轴
  • 共同度会变化

用非奇异变换矩阵QQ来得到f∗=QTf\mathbf{f}^* = Q^T\mathbf{f}，那么

Cov(f∗=QTIQ=QTQ≠I)Cov(\mathbf{f}^* = Q^TIQ = Q^TQ \neq I)

因此新的因子之间使相关的，不是正交的

聚类分析

无监督学习的分类，类别和个数及个体标签本身并不存在，通过相似性进行合理的聚集
对于nn个样本观测y1,y2,⋯ ,yn\mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_n，可计算距离矩阵

D=(dij)dij=d(yi,yj)D = (d_{ij}) \quad d_{ij} = d(\mathbf{y}_i, \mathbf{y}_j)

层级聚类

凝聚法

由单个个体开始，逐步合并最“相似”的个体，直到所有个体都合并为一个群组
层次聚类过程的结果可以利用图表展示为系统树图，用来展示层次聚类的每一个步骤及其结果，包括合并族群带来的距离的变化
凝聚法每一步需要合并“距离最小的两个族群”，不同族群间距离的定义方法决定了不同的聚类结果

  1. 建立nn个初始族群，每个族群中只有一个个体
  2. 计算nn个族群间的距离矩阵
  3. 合并距离最小的两个矩阵，计算新族群间的距离矩阵
  4. 重复步骤3直到只有一个族群
  5. 绘制系统树图
连接法
简单连接

定义族群间的距离为两族群中相隔最近的两个个体间的距离

D(A,B)=min⁡{d(yi,yj) for yi∈A AND yj∈B}D(A, B) = \min\lbrace d(\mathbf{y}_i, \mathbf{y}_j)\ \text{for}\ \mathbf{y}_i \in A\ \text{AND}\ \mathbf{y}_j \in B\rbrace

简单连接法存在“链式”问题，倾向于将新的个体归入已存在的族群，而不是创建新的族群

完全连接

定义族群间的距离为两族群中相隔最远的两个个体间的距离

D(A,B)=max⁡{d(yi,yj) for yi∈A AND yj∈B}D(A, B) = \max\lbrace d(\mathbf{y}_i, \mathbf{y}_j)\ \text{for}\ \mathbf{y}_i \in A\ \text{AND}\ \mathbf{y}_j \in B\rbrace

平均连接

定义族群间的距离为nAn_A个AA集合点和nBn_B个BB集合点产生的所有nAnBn_An_B个距离数值的平均

D(A,B)=1nAnB∑i=1nA∑j=1nBd(yi,yj)D(A, B) = \frac{1}{n_An_B}\sum^{n_A}_{i=1}\sum^{n_B}_{j=1}d(\mathbf{y}_i, \mathbf{y}_j)

质心连接

两族群的距离定义为两族群各自的质心，即样本均值向量之间的欧式距离

D(A,B)=d(y‾A,y‾B){y‾A=1nA=1nA∑i=1nAyiy‾B=1nB=1nB∑i=1nByiD(A, B) = d(\overline{\mathbf{y}}_A, \overline{\mathbf{y}}_B) \quad \begin{cases} \overline{\mathbf{y}}_A = \frac{1}{n_A} = \frac{1}{n_A}\sum^{n_A}_{i=1}\mathbf{y}_i \\ \overline{\mathbf{y}}_B = \frac{1}{n_B} = \frac{1}{n_B}\sum^{n_B}_{i=1}\mathbf{y}_i \end{cases}

合并后新的质心为

y‾AB=∑i=1nAyi+∑j=1nByjnA+nB=nAy‾A+nBy‾BnA+nB\overline{\mathbf{y}}_{AB} = \frac{\sum^{n_A}_{i=1}\mathbf{y}_i + \sum^{n_B}_{j=1}\mathbf{y}_j}{n_A + n_B} = \frac{n_A\overline{\mathbf{y}}_A + n_B\overline{\mathbf{y}}_B}{n_A + n_B}

如果两个族群合并之后，下一步合并时的最小距离反而减小，这种情况称为倒置，在系统树图中表现为交叉现象

基于中心质心连接

合并后新的质心为，不要加权平均

mAB=12(y‾A+t‾B)\mathbf{m}_{AB} = \frac{1}{2}(\overline{\mathbf{y}}_A + \overline{\mathbf{t}}_B)

Ward法

由合并前后的族群内方差平方和的差异定义距离

IAB=SSEAB−(SSEA+SSEB)I_{AB} = SSE_{AB} - (SSE_A + SSE_B)

SSEA=∑i=1nA(yi−y‾A)T(yi−y‾A) foryi∈ASSEB=∑i=1nB(yi−y‾B)T(yi−y‾B) foryi∈BSSEAB=∑i=1nA+nB(yi−y‾AB)T(yi−y‾AB) foryi∈ABy‾AB=(nAy‾A+nBy‾B)nA+nB\begin{aligned} SSE_A = \sum^{n_A}_{i=1}(\mathbf{y}_i - \overline{\mathbf{y}}_A)^T(\mathbf{y}_i - \overline{\mathbf{y}}_A)\ for \mathbf{y}_i \in A \\ SSE_B = \sum^{n_B}_{i=1}(\mathbf{y}_i - \overline{\mathbf{y}}_B)^T(\mathbf{y}_i - \overline{\mathbf{y}}_B)\ for \mathbf{y}_i \in B \\ SSE_{AB} = \sum^{n_A + n_B}_{i=1}(\mathbf{y}_i - \overline{\mathbf{y}}_{AB})^T(\mathbf{y}_i - \overline{\mathbf{y}}_{AB})\ for \mathbf{y}_i \in AB \\ \overline{\mathbf{y}}_{AB} = \frac{(n_A\overline{\mathbf{y}}_A + n_B\overline{\mathbf{y}}_B)}{n_A + n_B} \end{aligned}

合并合并之后方差增长小的族群

族群个数的选择

  • 可根据经验或业务解释预先设定
  • 也可由数据驱动：从系统树图中于给定距离水平下区分树图得到对应族群
  • 通常寻找合并组别时较大的距离变化的节点

分离法

凝聚法的反方向

K-均值聚类

层次聚类有点类似弹性算法，已分配群体不能再分配
非层次聚类：分割法

K-均值法试图寻找kk个族群(G1,G2,⋯ ,Gk)(G_1, G_2, \cdots, G_k)的划分方式，使得划分后的族群内方差（WGSS）最小

WGSS=∑l=ik∑i∈Gl∑j=1p(yij−y‾j(l))2=∑l=1k∑i∈Gl(yi−y‾i∈Gi(l))T(yi−y‾i∈Gi(l))\begin{aligned} \text{WGSS} &= \sum^k_{l=i}\sum_{i \in G_l}\sum^p_{j=1}(y_{ij} - \overline{y}^{(l)}_j)^2 \\ &= \sum^k_{l=1}\sum_{i \in G_l}(\mathbf{y}_i - \overline{\mathbf{y}}^{(l)}_{i\in G_i})^T(\mathbf{y}_i - \overline{\mathbf{y}}^{(l)}_{i\in G_i}) \end{aligned}

其中族群GlG_l中第jj个变量的均值

y‾j(l)=∑i∈Glyijniyi=(yi1,yi2,⋯ ,yip)Ty‾(l)=(y‾1(l),y‾2(l),⋯ ,y‾p(l))T\begin{aligned} \overline{y}^{(l)}_j &= \sum_{i \in G_l}\frac{y_{ij}}{n_i} \\ \mathbf{y}_i &= (y_{i1}, y_{i2}, \cdots, y_{ip})^T \\ \overline{\mathbf{y}}^{(l)} &= (\overline{y}^{(l)}_1, \overline{y}^{(l)}_2, \cdots, \overline{y}^{(l)}_p)^T \end{aligned}

  1. 选定kk个种子作为初始族群代表
  2. 每个个体归入距离其最近的种子所在的族群
  3. 归类完成后，将新产生的族群的质心定位新的种子
  4. 重复步骤2和3，直到不需要再移动

选取kk需要使WGSS足够小，但是不能最小的

用WGSS的碎石图来寻找最优的kk，通常选取拐点为最优的kk

选择初始种子

  • 在相互间隔超过某指定最小距离的前提下，随机选择kk个个体
  • 选择数据集前kk个相互间隔超过某指定最小距离个体
  • 选择kk个相互距离最远的个体
  • 选择kk个等距网格点，可能不是数据集的点

如果收敛速度极其缓慢或聚类结果每次都不同，可能数据原本就不存在族群

可以用层次聚类法聚类后，以各族群的质心作为kk-均值法的初始种子

参考