[学习笔记] - 信息安全

            graph LR
            plain_text--secret_key-->encryption-algorithm;
encryption-algorithm-->decryption-algorithm;
decryption-algorithm--secret_key-->decrypted_text;

密码系统

对称密钥模型

明文：plain text
密文：cipher text
密钥：key
加密算法：encipher
解密算法：decipher

可以用5元组表示(E, D, p, K, C)

基础假设：密码必须全寓与密钥

不能依赖算法不公开，这个系统是安全的。

密码分类

替代密码（Substitution）
置换密码（Transposition）
乘积密码（Product）

对称密钥密码（Symmetric）
非堆成密钥密码（Asymmetric）

分组密码（Block）
流密码（Stream）

设计好的密码

无条件安全：攻击者有无限的时间和计算资源也不能攻破算法（理论存在）
计算安全：攻击者的时间和资源是有限的假设下不能攻破

加密者的计算成本在攻击者不知道密钥的情况下破解的成本低就行了

在密文里，如何把明文的一些频率的统计规律给屏蔽掉
找key和明文一样长，不会循环使用
key在统计上和明文没有任何关系

Playfair密码

写下一个关键字
按照字母表顺序继续写(I和J不做区分)
进行分组
1. 2个字母一组
2. 对于重复字幕，或最后一个字母，进行填充
3. balloon -> ba lx lo on

MONAR
CHYBD
EFGIK
LPQST
UVWXZ

同行取右边
- ar -> rm
同列取下面
- mu -> cm
其他取交叉
- hs -> bp
- ea -> im

通过组合2个字母的表，就可以实现攻击

维吉尼亚密码

多字明表密码：我们有很多张字母表，根据Key选择不同的字母表进行加密

维吉尼亚密码每一行都是一个凯撒密码表

选一个key work
重复key到平文的长度
每一个平文按照key对应加密

1
2
3

key:        deceptivedeceptivedeceptive
text:       wearediscoveredsaveyourself
ciphertext: zicvtwqngrzgvtwavzhcqyglmgj

密钥是循环使用的，间隔一定周期后，会使用同样的字母表，知道了密钥的长度后，就可以攻击，找相同的字符串可以寻找
让key变得和明文一样长，这样的密码叫做Autokey Cipher（自动生成密钥密码）

Vernam密码

\begin{aligned} C_i &= P_i \oplus K_i \\ P_i &= C_i \oplus K_i \end{aligned}

$P_i$ ：明文的第 $i$ 个比特
$K_i$ ：密钥的第 $i$ 个比特
$C_i$ ：密文的第 $i$ 个比特

异或运算

A \oplus B = C \Rightarrow \begin{cases} A \oplus C &= B \\ B \oplus C &= A \end{cases}

置换密码

重新排列明文字母，达到信息加密的目的
与替换密码不同的是，原来明文中的字母同样出现在密文中顺序打乱

Rail Fence密码

明文：meet me after the toga party
顺序打乱，先纵向写2个字母，再横向写

1 2	m e m a t r h t g p r y e t e f e t e o a a t

密文：mematrhtgpryetefeteoaat

行置换密码

Key:      4 3 1 2 5 6 7
Plaintext a t t a c k p
          o s t o i n e
          d u n t i l t
          w o a m x y z

Ciphertext: TTNAAPTMTSUOAODWCOIXKNLYPETZ

填充（Padding）：如果出现字数不够，比如构不成行，就预先商量好填充字符

乘积密码

单次替换或置换方法构造密码技术并不安全
因此考虑联系多次使用简单的加密方法构造强密码
- 两次替换构成一个更复杂的替代密码
- 两次置换构成一个更复杂的置换密码
- 替代与置换的叠加同样
这是通向现代密码技术的基本道理

转子机

转子机是一种典型的乘积密码-古典密码的高峰
非常复杂的多轮替代技术

假设3个转子，根据3个转子，分类

快速转子
中速转子（快速转子转一轮 $\rightarrow$ 转一格）
慢速转子（中速转子转一轮 $\rightarrow$ 转一格）

总共有 $26^3$ 个字母表，所以有 $26^3$ 个字母表可以用来周期进行加密

公开密钥密码

在对称密钥密码的会话开始之前，双方需要交换密钥，这样就会进入一个死循环，所以我们需要一个可以公开密钥的密码

公钥：Public Key – 公开
私钥：Private Key – 保密

            graph LR
            plain_text--public_key-->encryption-algorithm;
encryption-algorithm-->decryption-algorithm;
decryption-algorithm--private_key-->decrypted_text;

非对称：通信双方地位不平等
- 私钥只有个人知道
应用数论的一些函数进行构造
补充而非取代堆成密钥密码技术
- 缺点：公钥密码的主要弱点是加密和解密速度慢

	RSA	Diffie-Hellman	DSA
保密通信	√	×	×
密钥交换	√	√	×
数字签名	√	×	√

公开密钥系统六要素

明文
公开密钥
私有密钥
加密算法
密文
解密算法

满足要求：

参与方B容易通过计算产生出一对密钥
发送方A很容易计算产生密文
接收方B通过计算解密密文
敌对方即使知道公开密钥，要确定私有密钥在计算上是不可行的
敌对方即使知道公开密钥和密文，在确定明文在计算上是不可行的
密钥对互相之间可以交换使用

数字签名

实现身份验证
不可否认

用私钥加密，如果通过公钥解密成功，则发送人只可能是拥有私钥的人

RSA密码

生成两个大素数 $p$ 和 $q$
计算这两个素数的乘积 $n = p \times q$
计算小于 $n$ 并且与 $n$ 互质的整数的个数，即欧拉函数 $\varphi(n) = (p-1)(q-1)$
选择一个随机数 $e$ 满足 $1 < e < \varphi(n)$ ，并且 $e$ 和 $\varphi(n)$ 互质，即 $\gcd(e, \varphi(n)) = 1$
解方程 $e \cdot d = 1 \pmod {\varphi(n)}$
公钥： $(e, n)$
私钥： $(d, n)$

简单C语言实现

// use gmp to deal with bignum
// complie with -lgmp option, ex: gcc -lgmp main.c
#include <gmp.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define mpz_rshift(a, b, c) mpz_tdiv_q_2exp(a, b, c)

typedef struct
{
    mpz_t n;
    mpz_t pub;
} Public;

typedef struct
{
    mpz_t n;
    mpz_t pri;
} Private;

// (a +/- b) % c = (a % c +/- b % c) % c
// (a * b) % c = (a % c) * (b % c) % c
// a^b % c = (a % c)^b % c
//
// b = b0 * 2^0 + b1 * 2^1 + b2 * 2^2 + b3 * 2^3 + ... + bn * 2^n
// a^b = a^{b0 * 2^0} * a^{b1 * 2^1} * a^{b2 * 2^2} * a^{b3 * 2^3} * ... * a^{bn * 2^n}
// a^b % c = a^{b0 * 2^0 % c} * a^{b1 * 2^1 % c} * a^{b2 * 2^2 % c} * a^{b3 * 2^3 % c} * ... * a^{bn * 2^n % c} % c
// a^b % c = a^{b1 * 2^1 % c} * a^{b2 * 2^2 % c} * a^{b3 * 2^3 % c} * ... * a^{bn * 2^n % c} % c
void encrypt(mpz_t encrypted, mpz_t msg, Public pub)
{
    mpz_t a, b, one, bone, res, aa;
    mpz_inits(a, b, one, bone, res, aa, (mpz_ptr)NULL);

    // init
    mpz_set_d(one, 1);
    mpz_set_d(res, 1);
    // a = msg
    mpz_set(a, msg);
    // b = pub.pub
    mpz_set(b, pub.pub);

    // b > 0
    while (mpz_cmp_d(b, 0) > 0)
    {
        // if (b & 1)
        // check b last == 1
        mpz_and(bone, b, one);
        if (mpz_cmp_d(bone, 0) != 0)
        {
            // res = res * a % pub.n
            mpz_mul(res, res, a);
            mpz_mod(res, res, pub.n);
        }

        // b = b >> 1 | 2 bin >> 1
        mpz_rshift(b, b, 1);

        // a = (a * a) % pub.n
        mpz_mul(aa, a, a);
        mpz_mod(a, aa, pub.n);
    }
    // encrypted = res
    mpz_set(encrypted, res);
}

// same as encrypt
void decrypt(mpz_t decrypted, mpz_t encrypted, Private pri)
{
    mpz_t a, b, one, bone, res, aa;
    mpz_inits(a, b, one, bone, res, aa, (mpz_ptr)NULL);

    // init
    mpz_set_d(one, 1);
    mpz_set_d(res, 1);
    // a = encrypted
    mpz_set(a, encrypted);
    // b = pri.pri
    mpz_set(b, pri.pri);

    // b > 0
    while (mpz_cmp_d(b, 0) > 0)
    {
        // if (b & 1)
        mpz_and(bone, b, one);
        if (mpz_cmp_d(bone, 0) != 0)
        {
            // res = res * a % pri.n
            mpz_mul(res, res, a);
            mpz_mod(res, res, pri.n);
        }

        // b = b >> 1
        mpz_rshift(b, b, 1);

        // a = (a * a) % pri.n
        mpz_mul(aa, a, a);
        mpz_mod(a, aa, pri.n);
    }
    // encrypted = res
    mpz_set(decrypted, res);
}

// Euclidean algorithm
void gcd(mpz_t r, mpz_t a, mpz_t b)
{
    mpz_t _a, _b, t;
    mpz_inits(_a, _b, t, (mpz_ptr)NULL);
    mpz_set(_a, a);
    mpz_set(_b, b);

    // b != 0
    while (mpz_cmp_d(_b, 0) != 0)
    {
        // t = b
        mpz_set(t, _b);
        // b = a % b
        mpz_mod(_b, _a, _b);
        // a = t
        mpz_set(_a, t);
    }
    mpz_set(r, _a);
}

// Extended Euclidean algorithm
void inverse(mpz_t d, mpz_t n, mpz_t phi)
{
    mpz_t a, b, x, y, x0, y0, q, temp;
    mpz_inits(a, b, x, y, x0, y0, q, temp, (mpz_ptr)NULL);

    // a = n
    mpz_set(a, n);
    // b = phi
    mpz_set(b, phi);

    // x = 0, x0 = 1
    // y = 1, y0 = 0
    mpz_set_d(x, 0);
    mpz_set_d(y, 1);
    mpz_set_d(x0, 1);
    mpz_set_d(y0, 0);

    mpz_t qx, qy;
    mpz_inits(qx, qy, (mpz_ptr)NULL);

    while (mpz_cmp_d(b, 0) != 0)
    {
        // q = a / b
        mpz_fdiv_q(q, a, b);
        // temp = a % b
        mpz_mod(temp, a, b);
        // a = b
        mpz_set(a, b);
        // b = temp
        mpz_set(b, temp);

        // temp = x
        mpz_set(temp, x);
        // x = x0 - q * x
        mpz_mul(qx, q, x);
        mpz_sub(x, x0, qx);
        // x0 = temp
        mpz_set(x0, temp);

        // temp = y
        mpz_set(temp, y);
        // x = x0 - q * x
        mpz_mul(qy, q, y);
        mpz_sub(y, y0, qy);
        // y0 = temp
        mpz_set(y0, temp);
    }

    // x0 < 0
    if (mpz_cmp_d(x0, 0) < 0)
        // x0 += phi
        mpz_add(x0, x0, phi);
    mpz_set(d, x0);
}

void hack(mpz_t hacked, mpz_t encrypted, Public pub)
{
    mpz_t p, q, pq, n, phi, e, d;
    mpz_inits(p, q, pq, n, phi, e, d, (mpz_ptr)NULL);

    // p = 2
    mpz_set_d(p, 2);
    mpz_set(n, pub.n);

    // Brute-force attack
    while (1)
    {
        mpz_fdiv_q(q, n, p);
        mpz_mul(pq, p ,q);
        if (mpz_cmp(pq, n) == 0)
            break;
        mpz_add_ui(p, p, 1);
    }

    // phi = (p - 1)(q - 1)
    mpz_t q1, p1, ephi_gcd;
    mpz_inits(q1, p1, ephi_gcd, (mpz_ptr)NULL);
    mpz_sub_ui(q1, q, 1);
    mpz_sub_ui(p1, p, 1);
    mpz_mul(phi, p1, q1);

    // calc d
    inverse(d, pub.pub, phi);

    // (n, d) private key
    Private pri = {*n, *d};

    // hack
    decrypt(hacked, encrypted, pri);

    printf("[hack result]\n");
    gmp_printf("p, q:      (%Zd, %Zd)\n", p, q);
    gmp_printf("phi:       %Zd\n", phi);
    gmp_printf("public:    (%Zd, %Zd)\n", pub.n, pub.pub);
    gmp_printf("private:   (%Zd, %Zd)\n", pri.n, pri.pri);
    gmp_printf("encrypted: %Zd\n", encrypted);
    gmp_printf("decrypted: %Zd\n", hacked);
}

int main(int argc, char const *argv[])
{
    // seed
    srand(time(0));

    mpz_t p, q, n, phi, e, d;
    mpz_inits(p, q, n, phi, e, d, (mpz_ptr)NULL);

    // set p, q
    mpz_set_d(p, 1000000007);
    mpz_set_d(q, 1000000009);

    // n = p * q
    mpz_mul(n, p, q);

    // phi = (p - 1)(q - 1)
    mpz_t q1, p1, ephi_gcd;
    mpz_inits(q1, p1, ephi_gcd, (mpz_ptr)NULL);
    mpz_sub_ui(q1, q, 1);
    mpz_sub_ui(p1, p, 1);
    mpz_mul(phi, p1, q1);

    // init rand e < 1000 << phi
    mpz_fdiv_q_ui(e, phi, rand() % 1000);
    while (mpz_cmp(e, phi) < 0)
    {
        // gcd(e, d) == 1 -> break
        gcd(ephi_gcd, e, phi);
        if (mpz_cmp_d(ephi_gcd, 1) == 0)
            break;

        // e += 1
        mpz_add_ui(e, e, 1);
    }

    // calc d
    inverse(d, e, phi);

    // (n, e) public  key
    Public pub = {*n, *e};
    // (n, d) private key
    Private pri = {*n, *d};

    // prepare
    mpz_t encrypted, decrypted, message;
    mpz_inits(encrypted, decrypted, message, (mpz_ptr)NULL);

    // init random message
    mpz_set_d(message, rand());
    // encrypt
    encrypt(encrypted, message, pub);
    // decrypt
    decrypt(decrypted, encrypted, pri);

    // result
    printf("[result]\n");
    gmp_printf("p, q:      (%Zd, %Zd)\n", p, q);
    gmp_printf("phi:       %Zd\n", phi);
    gmp_printf("public:    (%Zd, %Zd)\n", pub.n, pub.pub);
    gmp_printf("private:   (%Zd, %Zd)\n", pri.n, pri.pri);
    gmp_printf("message:   %Zd\n", message);
    gmp_printf("encrypted: %Zd\n", encrypted);
    gmp_printf("decrypted: %Zd\n", decrypted);

    // prepare hack
    mpz_t hacked;
    mpz_init(hacked);

    // start
    clock_t begin = clock();

    // hack
    hack(hacked, encrypted, pub);

    // end
    clock_t end = clock();

    // time
    double time_spent = (double)(end - begin) / CLOCKS_PER_SEC;
    printf("time: %lfs\n", time_spent);

    return 0;
}

使用模指数运算简化 $M^e \pmod n$

RSA加密时，明文以分组的方式加密：每一个分组的比特数应该小于 $\log_2n$ 比特，即： $M < n$
选取的素数 $p$ 和 $q$ 要足够大，从而乘积 $n$ 足够大，在事先不知道 $p$ 和 $q$ 的情况下分解 $n$ 是计算上不可行的

RSA算法的安全性

在理论上，RSA的安全性取决于模 $n$ 分解的困难性，目前最快的时间复杂度为 $O(e^{\sqrt{\ln(n)\ln(\ln(n))}})$
没有证明分解大数就是NP问题，对RSA的攻击困难程度不比大数分解难
RSA的一些变种算法已被证明等价于大数分解
由于是大数分解，RSA在最快的情况下也比DES慢几个数量级

RSA是目前最优秀的公钥方案之一

Diffie-Hellman密钥交换算法

是第一个公钥方案
使用在一些常用安全协议或产品（SSH）
密钥交换方案
- 不能直接用于有大量数据传输的保密通信
- 允许两个用户可以安全地建立一个共享的秘密信息，用于后续的通讯过程
- 该密码信息仅为两个参与者知道
算法的安全性依赖于有限域上计算离散对数的问题

通信双方/多方选择大素数 $p$ ，以及 $p$ 的一个原根 $a$
用户A选择一个随机数 $\text{X}_a < p$ ，计算 $\text{Y}_a = a^{\text{X}_a} \pmod p$
用户B选择一个随机数 $\text{X}_b < p$ ，计算 $\text{Y}_b = a^{\text{X}_b} \pmod p$
每一方保密X值，而将Y值交换给对方
双方获得一个共享密钥： $\text{K} = a^{\text{X}_a\text{X}_b}\pmod p$ $K = a^{X_{a} X_{b}} (m o d p)$
1. 对于用户 $A$ ，计算出 $\text{K} = Y_b^{\text{X}_a}\pmod p$
2. 对于用户 $B$ ，计算出 $\text{K} = Y_a^{\text{X}_b}\pmod p$

攻击者要获得K，需要求解离散对数

$p = 7, a = 3$
$X_a = 5 < 7, Y_a = 3^5\pmod 7 = 5$
$X_b = 2 < 7, Y_a = 3^2\pmod 7 = 2$
对于A: $K = 2^5\pmod 7 = 4$
对于B: $K = 5^2\pmod 7 = 4$

ElGamal加密算法

通信双方/多方选择大素数 $p$ ，以及 $p$ 的一个本原根 $a$ ，本原根的概念对应模q乘法群(需循环群)中的生成元
用户A
1. 选择一个随机数 $\text{X}_a < p - 1$
2. 计算 $\text{Y}_a = a^{\text{X}_a} \pmod p$
3. 私钥: $\text{X}_a$ ，公钥: $\lbrace q, a, Y_a \rbrace$
用户B
1. 选择一个随机数 $\text{X}_b < p - 1$
2. 计算私钥 $\text{Y}_b = (Y_a)^{\text{X}_b} \pmod p$
3. $C_1 = a^{X_b} \pmod p$
4. $C_2 = \text{Y}_b \times \text{M} \pmod p$
5. 发送 $(C_1, C_2)$
A收到明文对
1. 私钥 $\text{Y}_b = (C_1)^{\text{X}_a} \pmod p$
2. $M = C_2 \times \text{Y}_b^{-1} \pmod p$

椭圆曲线密码

Elliptic curve cryptography，缩写为 ECC，根据是有限域上的椭圆曲线上的点群中的离散对数问题 ECDLP。ECDLP 是比因子分解问题更难的问题，它是指数级的难度。

抗攻击性强
CPU占用少
内容使用少
网络消耗低
加密速度快

随着安全等级的增加，当前加密法的密钥长度也会成指数增加，而ECC密钥长度却只是成线性增加。例如，128位安全加密需要3072位RSA密钥，却只需要一个256位ECC密钥。增加到256位安全加密需要一个15360位RSA 密钥，却只需要一个512位ECE密钥。

//TODO

数论

模乘法群

对任意的正数 $m$ ，其既约剩余系关于模乘构成一个群，该群存在下面的性质：

封闭性：群中的任意元素 $a,b$ ， $c= a*b\pmod m$ ，则 $c$ 也在群中
逆元：若对任意的 $a$ 都存在 $b$ ，使得： $ab \equiv 1 \pmod m$ ，则称 $b$ 为 $a$ 的逆元，记为： $a^{-1}$

阶

阶的定义：设 $m > 1$ ，且 $\gcd(a, m) = 1$ (最大公约数)，那么使得 $a^r \equiv 1 \pmod m$ 成立的最小的正整数 $r$ 称为 $a$ 对模 $m$ 的阶，记为 $\delta_m(a)$ 。

\begin{aligned} 2^2 \equiv 1\pmod 3, 2\text{对模}3\text{的阶为}2 \\ 2^3 \equiv 1\pmod 7, 2\text{对模}7\text{的阶为}3 \end{aligned}

对于任意正整数 $a,m$ , 如果 $(a,m) = 1$ ,存在最小的正整数 $d$ 满足 $a^d \equiv1 \pmod m$ ，则有 $d$ 整除 $\varphi(m)$ ， $d$ 就是 $a$ 模 $m$ 的阶

原根

原根的定义：设 $m$ 为正整数， $a$ 为整数，如果满足 $a$ 对模 $m$ 的阶等于 $\varphi(m)$ (欧拉函数)，那么称 $a$ 为模 $m$ 的一个原根。

欧拉函数是小于或等于 $n$ 的正整数中与 $n$ 互质的数的数目

定理一
- 一个正整数m有原根的充要条件是 $m=2, 4, p^e, 2p^e$ ，其中， $p$ 奇素数， $e$ 为正整数。
定理二
- 每一个素数 $p$ 都有 $\varphi(p-1)$ 个原根，事实上，每一个正整数 $m$ 都有 $\varphi(\varphi(m))$ 个原根
定理三
- 若 $g$ 是 $m$ 的一个原根，则 $g,g^2,\cdots,g^{\varphi(m)}$
- 各数对 $m$ 取模的非负最小剩余就是小于 $m$ 且与 $m$ 互质的 $\varphi(m)$ 个数的一个排列。

原根的求法

首先求 $\varphi(m)$ 的素幂分解式：

\varphi(m) = p^{e_1}_1\times p^{e_2}_2 \times \cdots \times p^{e_k}_k

然后枚举 $g$ ，若恒满足

g^{\frac{\varphi(m)}{p_i}} \neq 1(mod\ m) \quad i=1,2,...,k

则 $g$ 是 $m$ 的一个原根。

原根例子

设 $m = 7$ ，则 $\varphi(7)$ 等于 $6$
设 $a = 2$ $a = 2$ ，由于
- $2^3 \equiv 1\pmod 7$
- $2^6 \equiv 1\pmod 7$
- 它们相等了，所以 $2$ 不是模 $7$ 的一个原根。设 $a = 3$ ，由于
- $3^1 \equiv 3\pmod 7$
- $3^2 \equiv 2\pmod 7$
- $3^3 \equiv 6\pmod 7$
- $3^4 \equiv 4\pmod 7$
- $3^5 \equiv 5\pmod 7$
- $3^6 \equiv 1\pmod 7$
- 全部不相同，所以 $3$ 是模 $7$ 的一个原根。

离散对数

设 $g$ 为素数 $p$ 的模循环群的原根，对任意的 $a$ ，计算：

b=g^a \pmod p

是容易的（通过幂取模算法）。反过来，给定 $b$ 计算满足（1）式的 $a$ 是非常困难的， $a$ 称为以 $g$ 为基 $b$ 的离散对数。如果只是实数领域的指数运算，则可解出 $a = \log_gb$ ，因为取模运算导致上式无法表达为该形式，但仍称 $a$ 为离散对数

因为 $a, b$ 均为整数，不像实数那么"连续"，故称离散对数。
因为限定 $a, b$ 都属于模 $p$ 的循环群，而该群的大小为： $\phi(p)=p-1$ ，故称"有限域"上的离散对数

费马小定理

若 $p$ 是素数, $a$ 是正整数且不能被 $p$ 整除, 则 $a^{p-1} \equiv 1 \pmod p$

a^p \equiv a\pmod p

假定集合 $\lbrace 1, 2, \cdots, p - 1 \rbrace$ ， $p$ 与每一个元素都互质
对每一个元素，我们都 $\times a \% p$ ，得到

\lbrace a\ \%\ p, 2a\ \%\ p, \cdots, (p - 1)a\ \%\ p\rbrace

很明显，原本元素就互质乘上不能被 $p$ 整除的 $a$ ，依旧不能被整除，所以新的集合中所有的元素都不等于 $0$ 并且各个元素都不相等，其差不是p的倍数（所以不会有相同余数）。说明2个集合的元素相同，只是顺序不同。

若n不能整除 $a-b$ ， $x>0$ ， $(x,n)=1$ ，则 $n$ 也不能整除 $x(a-b)$

因此

\begin{aligned} 1 \cdot 2 \cdot 3 \cdots (p - 1)\pmod p &= a \cdot 2a \cdot 3a \cdots (p - 1)a\pmod p \\ &= W \cdot a^{p-1}\pmod p \end{aligned}

因为 $W = 1 \cdot 2 \cdot 3 \cdots (p - 1)$ ，且 $\gcd(W, p) = 1$ ，所以可以得到

a^{p-1} \equiv 1 \pmod p

欧拉定理

若 $n,a$ 为正整数，且 $n,a$ 互素（即 $\gcd(a, n)=1$ ），则

a^{\varphi (n)}\equiv 1{\pmod n}

即 $a^{\varphi (n)}$ 与 $1$ 在模 $n$ 下同余, $\varphi(n)$ 为欧拉函数

证明：

所有与 $n$ 互质的同余类构成一个群，些同余类构成一个群，称为整数模 $n$ 乘法群，因为此群阶为 $\varphi(n)$ ，所以 $a^{\varphi (n)}\equiv 1{\pmod n}$ 。

当 $n$ 是素数的时候， $\varphi(n)= n - 1$

单向函数

对于一个函数 $f(x)$ ，如果对于其定义域上的任意 $x$ ， $f(x)$ 都容易计算，同时，对于其值域中几乎所有的取值 $y$ ，计算其逆函数 $f^{-1}(y)$ 都是不可行的，则函数 $f(x)$ 被称为单向函数

可以提供单向函数的三大数学难题

大整数分解问题（IFP）
离散对数问题（DLP）
椭圆曲线离散对数问题（ECDLP）

单向陷门函数

对于一个单向函数 $f(x)$ ，如果其逆函数 $f^{-1}(y)$ 在已知某些辅助信息的情况下容易求解得出，则称该单向函数 $f(x)$ 为单向陷门函数

构造公钥密码系统的关键是如何在求解某个单向函数的逆函数的NP完全问题中设置合理的陷门

报文鉴别

安全服务与安全需求

通信保密不能概括所有安全需求
- 保密性（Confidentiality）
  - 防止未经授权的访问
- 完整性（Integrity）
  - 防止未经授权的修改
- 可用性（Availablilty）
  - 在任何时候，合法用户的访问请求可以被允许
- 可认证（Authentication）
  - 可认证我们通信的人的身份
- 抗否认（Non-repudiation）
  - 通信发生之后，不能抵赖发过这个报文

ITSEC：Information Technology Security Evaluation Criteria

报文鉴别安全需求

泄密
流量分析
修改内容
破坏数据包收到的先后顺序
不承认发送过某个报文
冒名顶替
浏览器网银

保护报文的完整性
- 报文加密
验证发送者的身份
- 报文鉴别码
抗抵赖：防止报文发送者抵赖
- HASH函数

对称密钥报文加密

报文加密在提供保密性的同时，本身也能提供某些报文假别的安全服务

英文只有发生在和接收者知道这个对称密钥
接收者知道发送者创建了他
知道报文内容在通信过程中没有被篡改

不能提供抗抵赖

非对称密钥报文加密

公钥加密：

无法实现报文鉴别所包括的任何一项安全服务：因为任何人都知道公钥，只能提供保密性

私钥加密：

不具备保密性：因为任何人都知道公钥，但是可以实现报文鉴别的所有需求

完整性，需要特定的格式
证实发送者的身份
每一方都可以用 $PU_a$ 验证签名

叠加使用：用私钥对报文签名，然后使用接收者的公钥加密

同时提供保密性和报文鉴别的所有三种安全服务
代价是需要使用俩个公钥

	保密性	完整性	可认证	抗抵赖
公钥加密	√
私钥加密		√	√	√
共私钥加密	√	√	√	√

报文鉴别码

加密整个报文，开销较大

报文鉴别码
- 固定长度比特串
- 由报文鉴别码算法生成
  - 算法的输入包括：报文和密钥
  - 算法设计类似于对称密钥加密，但不可逆
- 附加到报文上用于报文鉴别
接收者对报文执行相同方向的计算并检查它是否与收到的MAC匹配
确保报文来自声称的发送者且传输过程中没被篡改

$A \rightarrow B: M||C(K, M)$ $A \to B : M ∣ ∣ C (K, M)$
- 完整性
- 可验证
- 因为使用对称密钥，不能抗抵赖
$A \rightarrow B: E(K_2, M||C(K_1, M))$ $A \to B : E (K_{2}, M ∣ ∣ C (K_{1}, M))$ : 先计算明文的鉴别码，再加密
- 完整性
- 可验证
- 不能抗抵赖
- 保密性
$A \rightarrow B: E(K_2, M) || C(K_1, E(K_2, M))$ $A \to B : E (K_{2}, M) ∣ ∣ C (K_{1}, E (K_{2}, M))$ : 先加密，再计算密文的鉴别码
- 完整性
- 可验证
- 不能抗抵赖
- 保密性

报文鉴别码无法实现抗抵赖

对报文的攻击： $M' \neq M, C_K(M') = C_K(M)$
MAC应该均匀分布
MAC应该影响报文的每一位

哈希函数

将任意长度的报文压缩到固定长度的二进制串
通常哈希函数是公开且没有密钥
用于检测报文是否被更改
经常用于创建数字签名

哈希函数要求

可应用于任意大小的报文M
生成固定长度的输出h
很容易计算报文M的哈希值
已知哈希值，不能计算得到x（单向性）
弱抗碰撞性
强抗碰撞性

哈希函数应用

            graph LR
            报文--hash-->哈希值
报文-->合并
哈希值-->合并
合并--私钥-->接受者
接受者--私钥-->解密
解密--计算报文哈希值-->结果
解密--哈希值-->比较
结果-->比较

保密性
完整性
可认证

            graph LR
            报文--hash-->哈希值
哈希值--对称密钥加密-->加密哈希值
报文-->合并
加密哈希值-->合并
合并-->接受者
接受者--对称密钥加密哈希值-->结果1
接受者--计算报文哈希值-->结果2
结果1-->比较
结果2-->比较

完整性
可验证

            graph LR
            报文--hash-->哈希值
哈希值--私钥加密-->加密哈希值
报文-->合并
加密哈希值-->合并
合并-->接受者
接受者--公钥解密加密哈希值-->结果1
接受者--计算报文哈希值-->结果2
结果1-->比较
结果2-->比较

完整性
可验证
抗抵赖

            graph LR
            报文--hash-->哈希值
哈希值--私钥加密-->加密哈希值
报文-->合并
加密哈希值-->合并
合并--对称密钥-->接受者
接受者--对称密钥-->解密
解密--计算报文哈希值-->结果1
解密-->加密哈希值1
加密哈希值1--公钥-->结果2
结果1-->比较
结果2-->比较

保密性
完整性
可验证
抗抵赖

            graph LR
            报文-->合并
随机数--hash-->哈希值
哈希值-->合并
合并-->接受者
接受者--计算随机数哈希值-->结果1
接受者-->哈希值1
哈希值1-->比较
结果1-->比较

完整性
可验证

用于口令文件等等

            graph LR
            报文-->合并
随机数--hash-->哈希值
哈希值-->合并
合并--对称密钥-->接受者
接受者--对称密钥-->解密
解密--计算随机数哈希值-->结果1
解密-->哈希值1
哈希值1-->比较
结果1-->比较

保密性
完整性
可验证

哈希函数实现

将报文分组，报文分组异或运算的结果作为哈希值

可以防止随机的报文比特错，但不够安全

哈希算法的一般结构：利用分组，通过上一个hash结构，并加上当前段的内容，进行hash到最后一组
常见Hash

MD5
SHA1
- SHA-256
- SHA-384
- SHA-512
RIPEMD-160

生日攻击

找到具有相同生日的两个人与找到哈希碰撞时一回事，当有30个人的时候，两人生日相同概览大概为75%

泰勒展开：

\begin{aligned} e^x &= 1 + x + \frac{x^2}{2!} + ... \approx 1 + x \\ (1 - \frac{n}{356}) = e^{\frac{n}{356}} \end{aligned}

n个人生日不相同的概览为

\begin{aligned} \approx& 1 \cdot e^{\frac{-1}{356}} \cdot e^{\frac{-2}{356}} \cdots e^{\frac{-n + 1}{356}} \\ =& e^{-\frac{1+2+3+\cdots+(n-1)}{365}} \\ =& e^{-\frac{n(n - 1)}{2 * 365}} \\ =& e^{-\frac{n(n - 1)}{730}} \end{aligned}

至少两个人生日相同概率为：

1 - e^{\frac{-n^2}{730}}

更一般的：N个对象，选择r个

P(\text{same}) = 1 - e^{\frac{-r^2}{2N}}

选择

\frac{r^2}{2N} = \ln(2)

当 $r \approx 1.177\sqrt{N}$ ，那么2人选择同一对象概率为50%
当有N个可能性，我们有一个 $\sqrt{N}$ 个元素，则匹配可能性为50%

哈希函数的输出不够大，可以使用生日攻击来哈希碰撞

Web和电子商务

Web外网可见
复杂的软件会隐藏漏洞
Web占用容易配置
可作为跳板进行内网攻击
没有威胁意识存在

SSL/TLS协议

在传输层加密

在应用层加固
- 把加密的步骤交给程序员
在网络层/传输层
- 可以作为公共服务
- SSL只能在主机上实现
- IPsec可以在路由器上实现

安全套接字协议SSL有3个版本

V1.0
V2.0
V3.0

称为Internet标准后，改名为TLS，TLS的第一版可以认为是SSL V3.1

SSL/TLS子协议

底层：SSL记录协议
- 建立在可靠的传输协议之上
- 提供连接的安全性
  - 保密性
  - 完整性
- 用来封装高层协议
上层：
- SSL握手协议
  - 客户和故武器之间相互认证
  - 协商加密算法和密钥
  - 它提供连接安全性
    - 身份认证，至少对一方实现认证，也可双向
    - 协商得到的共享密钥是安全的，中间人不能知道
    - 协商过程是可靠的
- SSL密码变换协议
- SSL警告协议

SSL工作流程

先握手
- 单项身份认证，双向认证
- 协商SSL会话密钥等
SSL记录协议
- 加密会话数据
- 提供完整性，保密性支持

struct {
  ContentType type;
  ProtocolVersion version;
  uint16 length;

  EncryptedData fragment;
} SSLCiphertext;

            sequenceDiagram
            autonumber
client->>server: client_hello
server->>client: server_hello

交换Hello消息，对于算法，交换随机值等协商一致

client_hello
- 版本
- 随机数（32位为时间戳+28位随机序列）
- 会话ID
- 客户支持密码算法列表
- 客户支持压缩方法列表

            sequenceDiagram
            server->>client: certificate
server->>client: server_key_exchange
server->>client: certificate_request
server->>client: server_hello_done

certificate: 如果已经有证书了就不需要
server_key_exchange: 协商不一致
certificate_request: 需要对客户机进行认证

            sequenceDiagram
            client->>server: certificate
client->>server: client_key_exchange
client->>server: certificate_verify

certificate: 上一阶段如果有server_key_exchange
certificate_verify: 如果需要对客户机进行认证
client_key_exchange: 完成密钥的交换
- 用server的公钥加密一个对称密钥
- 用这个对称密钥进行大量通信

            sequenceDiagram
            client->>server: change_cipher_spec
client->>server: finished
server->>client: change_cipher_spec
server->>client: finished

SET协议

开放的安全电子交易安全规范
保护Internet上的信用卡支付交易
一系列安全协议与规范

因为太复杂了，后续系统都是根据其子集进行设计的

通过安全的交易通道
- 保密性
- 完整性
基于X.509证书提供交易方之间的信任
- 基于公钥密码实现身份认证
强调隐私保护
- 仅限参与方能获取自己知道的信息

双重数字签名

            graph LR
            PI--Hash-->PIMD-->合并--Hash-->POMD-->E-->Dual_Signature
OI--Hash-->OIMD-->合并
KRc-->E

PI: 支付信息
OI: 订单信息
PIMD: 支付信息哈希结果
OIMD: 订单信息哈希结果
POMD: 支付信息和订单信息的哈希结果
KRc: 客户（cikaren）私钥

公开密钥基础设置PKI

如何提供数字签名功能
如果实现不可否认的服务
公钥和身份如果建立联系
- 为什么要相信这是某个人的公钥
- 公钥的权限
公钥如何管理

数字证书：实现身份和公钥绑定
需要具有公信力的第三方进行证明
- CA（Certification Authority）

数字证书结构

主体身份信息
主体的公钥
CA名称
CA签名

            graph LR
            主体身份信息-->合并
主体的公钥-->合并
CA名称-->合并
合并--Hash-->CA签名

PKI

用公钥的原理和技术实施和提供安全服务的具有普适性的安全基础设施

证书授权中心（CA）
证书库
证书注销
密钥备份和恢复
自动密钥更新
密钥历史档案
交叉认证
支持不可否认
时间戳
客户端软件

数字证书格式

证书（certificate），简称为cert

证书是一个机构颁发给一个安全主题的证明，所以证书的权威性取决于该机构的权威性
一个证书中，最重要的信息是主体的名字，主体的公钥，机构的签名，算法和用途
签名的证书和加密证书公开
最常用的证书格式是：X.509.v3

            classDiagram
            class X509
  X509 : Version
  X509 : -----------
  X509 : Certificate Serial Number
  X509 : -----------
  X509 : algorithm
  X509 : parameters
  X509 : -----------
  X509 : Issuer Name
  X509 : -----------
  X509 : not before
  X509 : not after
  X509 : -----------
  X509 : Subject Name
  X509 : -----------
  X509 : algorithm
  X509 : parameters
  X509 : key
  X509 : -----version1------
  X509 : Issuer Unique Identifier
  X509 : -----------
  X509 : Subject Unique Identifier
  X509 : -----version2------
  X509 : Extensions
  X509 : -----version3------
  X509 : algorithm
  X509 : parameters
  X509 : encrypted

PKI信任关系

当一个安全主体看到另外一个安全主体出示证书时，它是否信任此证书
可信CA
- 如果一个主体假设CA能够建立并维持一个准确的"主体-公钥属性"之间的绑定，则他可以信任该CA
信任模型
- 基于层次结构的信任模型
- 交叉认证

对于一个运行CA的大型权威机构而言，签发证书的工作不能仅仅由一个CA来完成，可以建立一个CA层次结构

根CA
- 中间CA
  - 叶CA

根CA具有一个自签名的证书
根CA依次对它下面的CA进行签名
层次结构中叶子节点上的CA用于对安全主体进行签名
对于主体而言，它需要信任根CA，中间的CA可以不必关系，同时它的证书是由底层CA签发的
在CA的机构中，需要维护这棵树
- 在每个节点CA上，需要保护两种cert
  - Forward Certificates：其他CA发给它的certs
  - Reverse Certificates：它发给其他CA的certs

两个CA进行信任

一个CA承认另外一个CA在一定名字空间范围内的所有被授权签发的证书
- 单向交叉认证
- 双向交叉认证
交叉认证的约束
- 名字约束
- 路径长度约束
- 策略约束

身份认证

宣称者向验证方出示证据，证明其身份的交互过程
至少涉及两个参与者
分为：双向认证，单项认证

身份认证具有实时性，动态的，需要保证身份验证的鲜活性，对于身份认证的攻击为"重放攻击"

身份认证基本方法

宣称者所知道的
宣称者所拥有的
宣称者的生物特征

用短的PIN码锁住长的密钥

基于口令的身份认证

初始化阶段
- 设置密码
- 哈希密码储存
身份认证阶段
- 用户登录
- 计算比较哈希

攻击：

重放攻击
穷举攻击
字典攻击
- 在线字典攻击
- 离线字典攻击

撒盐防攻击

动态口令

基本实现：利用hash函数不断hash上一次的hash值，或者采用其他的算法。

质问与应答的基本逻辑

B要完成对A的认证

身份认证基于A所知道的密码
首先B给A发生一个随机数
A收到后，作某种变换，返回回复
回复同时依赖于随机数和知道的密码
B收到后，即可验证

在有的协议中，这个chanllenge也称为Nonce
A生成的Response报文的典型变换有

A的密钥加密，说明A知道这个密钥
有时会对challenge简单运算，比如+1，在做加密处理

使用对称密钥

            sequenceDiagram
            Bob->>Alice: Challenge
Alice->>Bob: Alice, E(K, Challenge)
Bob->>Alice: OK

单项身份认证

$Bob \rightarrow Alice: r_b$
$Alice \rightarrow Bob: E_K(r_b, B)$
检测 $r_b$ ，和 $B$ （标记了报文的方向）
$r_b$ 要求不能重复

反射攻击时对质疑-应答身份认证协议的一种攻击方式，攻击者在两个方向上使用相同的协议，也就是说，攻击者让服务器对自己这个方向进行Challenge

使用时间戳

$Alice \rightarrow Bob: E_k(T, B)$ $A l i c e \to B o b : E_{k} (T, B)$
- $T$ : Alice的本地时钟当前的时间戳
Bob解密后检验时间戳是否课接受

双向认证

$Bob \rightarrow Alice: r_b$
$Alice \rightarrow Bob: E_k(r_a, r_b, B)$
$Bob \rightarrow Alice: E(r_a, r_b)$

要求参与方实现完成对称密钥的交换，可扩展性是个问题

使用报文鉴别码

$MAC = h_K(M)$ ， $M$ 是报文

接收方检验：同样的方法计算收到报文的MAC值，与收到的MAC值比对

$Bob \rightarrow Alice: r_b$
$Alice \rightarrow Bob: r_a, H_k(r_a, r_b, B)$
$Bob \rightarrow Alice: H_K(r_a, r_b, A)$

单向认证

$Bob \rightarrow Alice: r_b$
$Alice \rightarrow Bob: r_a, H_k(r_a, r_b, B)$

使用公开密钥

$Bob \rightarrow Alice: r_b$
$Alice \rightarrow Bob: cert_a, r_a, B, S_a(r_a, r_b, B)$
Bob进行验证
- 用公钥证书里的公钥验证A的签名
- 参数B标记报文方向
- 随机数 $r_a$ 防止选择文本攻击

基于时间戳： $Alice \rightarrow Bob: cert_a, t_a, B, PR_a(t_a, B)$

双向认证

$Bob \rightarrow Alice: r_b$
$Alice \rightarrow Bob: cert_a, r_a, B, S_a(r_a, r_b, B)$
$Bob \rightarrow Alice: cert_b, A, S_b(r_a, r_b, A)$

Needham-Schroeder协议

假设n个通信参与者

没有可信的第三方，需要 $n(n-1)/2$ 个对称密钥
如果有，只需要 $n-1$ 个对称密钥

基于可信第三方实现密钥分发与身份认证的协议
协议种，可信第三方记作Trent
Trent又被称作是密钥分发中心
- 生成密码，一次会话一个密钥
使用Trent的服务，可以实现任何两个最终用户之间的安全通信
会话结束后，可以完全放弃密钥

前提：

Alice和Trent又共享的对称密钥 $K_{AT}$
Bob和Trent又共享的对称密钥 $K_{BT}$

            sequenceDiagram
            Alice->>Trent: 随机数Na，Bob
Note right of Trent: 生成随机数K
Trent->>Alice: {Na, K, Bob, {K, ALice}_KBT}_KAT
Note right of Alice: 解密，检查Na
Alice->>Bob: Trent, {K, Alice}_KBT
Note right of Bob: 解密，生成Nb
Bob->>Alice: {I'm Bob! Nb}_K
Alice->>Bob: {I'm Alice! Nb - 1}_K

在步骤3可以进行中间人攻击，没有保证报文的鲜活性

            sequenceDiagram
            Alice->>Trent: 随机数Na，Bob
Note right of Trent: 生成随机数K
Trent->>Alice: {Na, K, T, Bob, {K, ALice}_KBT}_KAT
Note right of Alice: 解密，检查Na
Alice->>Bob: Trent, {K, Alice, T}_KBT
Note right of Bob: 解密，生成Nb
Bob->>Alice: {I'm Bob! Nb}_K
Alice->>Bob: {I'm Alice! Nb - 1}_K

Kerbeos协议

基于一个集中的认证服务器AS，把各个应用服务器上共有的认证功能抽象剥离，集中到AS上
利用对称密钥实现，没有使用公开密钥

最早的单点登录SSO

解决的问题：分布式环境下的认证

用户伪装另外一个用户访问服务器
用户更改工作站的网络地址
用户窃听报文交换过程，利用重放攻击进入服务器

Kerbeos符合

C: 客户
AS: 认证服务器（存放所有用户口令）
V: 服务器
IDc: 在C上的用户标识符
IDv: V的标识符
Pc: 在C上的用户口令
ADc: C的网络地址
Kv: AS和V共享的加密密钥

Kerbeos引入协议

            sequenceDiagram
            C->>AS: IDc, Pc, IDv
Note right of AS: Ticket=E_Kv(IDc, ADc, IDv)
AS->>C: Ticket
C->>AS: IDc, Tickeet

要求用户频繁输入口令
申请不同服务。用户需要新的票据
口令是明文传输

增加票据许可服务器TGS，剥离授权功能

            sequenceDiagram
            C->>AS: IDc, IDtgs
Note right of AS: E_Kv: Hashed user 
password as secret key
AS->>C: E_Kc(Ticket_tgs)
C->>TGS: IDc, IDv, Ticket_tgs
TGS->>C: Ticket_v
C->>V: IDc, Ticket_v

$\text{Ticket}_{tgs} = \text{E}_{\text{K}_{tgs}}(\text{ID}_c, \text{AD}_c, \text{ID}_{tgs}, \text{TS}_1, \text{Lifetime}_1)$
$\text{Ticket}_v = \text{E}_{K_v}(\text{ID}_c, \text{AD}_c, \text{ID}_v, \text{TS}_2, \text{Lifetime}_2)$

通过TGS进行每一个服务器的授权， $\text{Lifetime}_1 > \text{Lifetime}_2$

事先共享

            graph LR
            客户机C--用户口令-->认证服务器AS
认证服务器AS--用户口令-->客户机C
认证服务器AS--K_tgs-->TGS
TGS--K_tgs-->认证服务器AS
TGS-->K_v-->V
V-->K_v-->TGS

每一张Ticket的有效期的设置
- 太短：用户频繁认证
- 太长：重放攻击
可能被窃取 $\text{Ticket}_v$
服务器无法向用户认证自己

Kerbeos完整协议

$\text{K}_v$ : TGS和V的共享加密密钥
$\text{K}_{tgs}$ : TGS和AS的共享加密密钥

客户机的密钥可以通过计算客户机口令的单向函数得到
每个客户机与AS有共享的密码-客户机密钥
TGS与AS有共享的对称密钥 $\text{K}_{tgs}$
每个应用服务器都与TGS有共享的对称密钥 $\text{K}_v$

            sequenceDiagram
            C->>AS: IDc, IDtgs, TS_1
Note right of AS: K_c,tgs: AS服务器给
C和TGS的会话密钥
AS->>C: E_Kc(K_c,tgs, ID_tgs, TS_2, Lifetime_2, Ticket_tgs)
C->>TGS: IDv, Ticket_tgs, Authenticator_c
Note right of C: Authenticator_c:
E_Kc,tgs(IDc, ADc, TS_3)
TGS->>C: E_Kc,tgs(K_c,v, IDv, TS_4, Ticket_v)
C->>V: Ticket_v, Authenticator_c
V->>C: E_Kc,v(TS_5 + 1)

$\text{Ticket}_{tgs} = \text{E}_{\text{K}_{tgs}}(\text{K}_{c,tgs}, \text{ID}_c, \text{AD}_c, \text{ID}_{tgs}, \text{TS}_2, \text{Lifetime}_2)$
$\text{Ticket}_v = \text{E}_{K_v}(\text{K}_{c,v}, \text{ID}_c, \text{AD}_c, \text{ID}_v, \text{TS}_4, \text{Lifetime}_4)$
$\text{Authenticator}_c = \text{E}_{\text{K}_{c,v}}(\text{ID}_c, \text{AD}_c, \text{TS}_5)$ $Authenticator_{c} = E_{K_{c, v}} (ID_{c}, AD_{c}, TS_{5})$
- 完成对C的认证，避免重放攻击

            sequenceDiagram
            C->>AS: 请求认证
AS->>C: 颁发Ticket_tgs
C->>TGS: 请求V的服务
TGS->>C: 颁发Ticket_v
C->>V: 发送Ticket_v
V->>C: 向C证明V的身份

区块链

面向数字货币记账系统设计的密码解决方案

无比特币不谈区块链

账本公开机制: 每人手里都可有一份账本，都是真的
账本上不再记载每户参与者的余额，而只记载每一笔交易
- 即记载每一笔交易的付款人，收款人，付款金额
- 只要账本的初始状态确定，每一笔交易记录可靠并有序，每个人的持有金额可以推算出来
账本由私有改为公开，只要任何参与者需要，都可以获得当前完整的账本，账本上记录了从账本创建开始到当前所有的交易记录
基本假设: 大家都必须诚实守信，或者说一半以上的人需要诚实守信，即承认真的账本确实是真的，即使有少部分人集体伪造账本，也不会被替代

区块

区块链的实质: 账本就是比特币系统中的区块，多个区块连接在一起就是区块链
一个区块记录着多笔交易
区块是有顺序的，一个区块会有唯一的夫区块
区块和区块链最重要的安全需求: 完整性

比特币完整性

交易历史的完整性
- 整个账本链条的完整性
  - 交易发送后不可逆，交易历史记录完整，可追溯
交易本身的完整性
- 账本上所有交易记录完整
  - 不可篡改

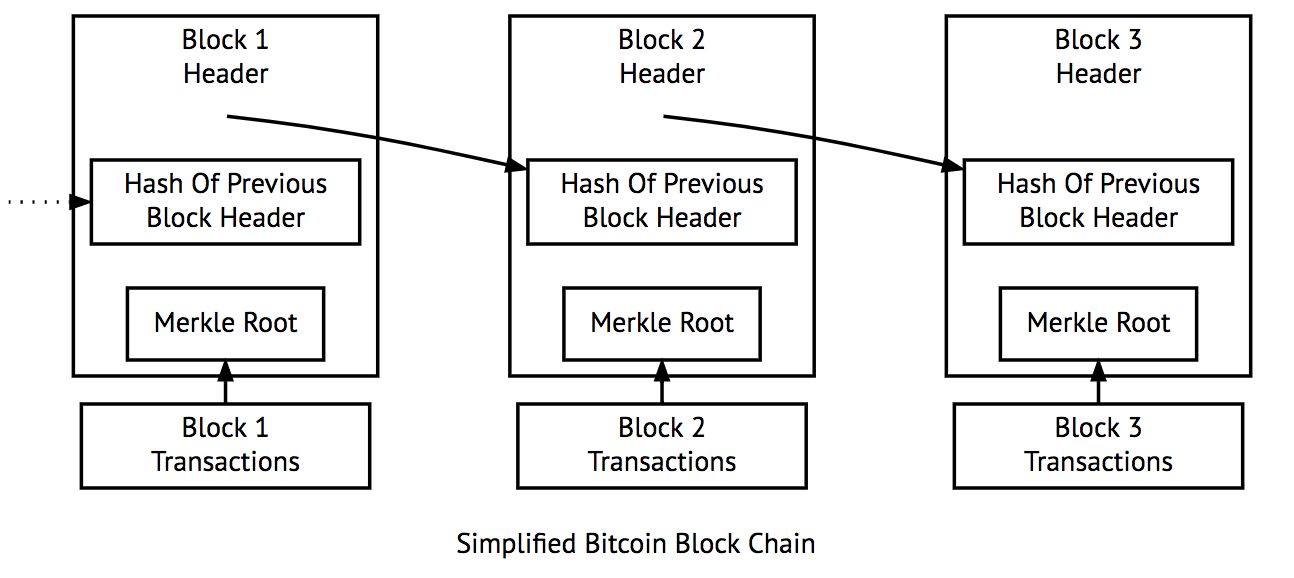
            graph LR
            区块头-->区块体

区块头
- 记录当前区块的元信息
- 前一区块头Hash: 交易历史的完整性
- Merkle树根Hash: 交易本身的完整性
区块提
- 记录实际交易数据

字节长度	字段	说明
4	区块版本号	区块版本号
32	前一区块头Hash	前一个区块头的哈希值
32	Merkle树根Hash	交易列表生成的默克尔树根哈希
4	时间戳	该区块产生的近似事件
4	难度目标	难度目标，挖矿难度值
4	Nonce	挖矿过程中使用的随机值

            graph LR
            区块8--SHA-256-->区块1--SHA-256-->区块2

Merkle树

Merkle树是一种Hash二叉树，它是一种用作快速归纳和校验大规模数据完整性的数据结构
生成整个交易集合的数字指纹，提供了一种校验区块是否存在某交易的高效途径
至多计算 $2\log_2(N)$ 次就能查询出任意某数据元素是否在该树中，该数据结构非常高效
在比特币的Merkle树中，交易被两次使用SHA-256算法，称为double-SHA256

Merkle根: 实质上是整个交易集合的Hash

            graph LR
            HA-->H_AB
HB-->H_AB

$H_A = \text{SHA256}(\text{SHA256}(A))$
$H_{AB} = \text{SHA256}(\text{SHA256}(H_A + H_B))$

其中A为Block Header

# Version
ver = 1
# Persious BLock Hash
prev_block = "000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f"
# Merkle Root
mrkl_root = "0e3e2357e806b6cdb1f70b54c3a3a17b6714ee1f0e68bebb44a74b1efd512098"
# Timestamp
time = 1231469665
# Difficulty Target
bits = 486604799
# Nonce
nonce = 2573394689

def deal_str(big_endian):
    # [::-1] 改变字节序
    return big_endian.decode("hex")[::-1]

def deal_int(n):
    # < 代表小端序
    # L 代表 unsigned long
    return struct.pack("<L", n)

header_bin = deal_int(ver) + deal_str(prev_block) + deal_str(mrkl_root) + deal_int(time) + deal_int(bits) + deal_int(nonce)
# 两次 sha256
hash = hashlib.sha256(hashlib.sha256(header_bin).digest()).digest()
# 大端序
cur_block = hash[::-1].encode('hex')
# 结果
print(cur_block)

区块数据结构

            classDiagram
            class Block
  Block : BlockSize
  Block : Hash
  Block : BlockHeader
  Block : Transaction Counter
  Block : Transactions

class Transaction
  Transaction : Version
  Transaction : Input Counter
  Transaction : Inputs
  Transaction : Output Counter
  Transaction : Outputs
  Transaction : Lock time

class BlockHeader
  BlockHeader : Version
  BlockHeader : Persious BLock Hash
  BlockHeader : Merkle Root
  BlockHeader : Timestamp
  BlockHeader : Difficulty Target
  BlockHeader : Nonce

class TransactionInput
  TransactionInput : Transaction Hash
  TransactionInput : Output Index
  TransactionInput : Unlocking-Script Size
  TransactionInput : Unlocking-Script
  TransactionInput : Sequence Number

class TransactionOutput
  TransactionOutput : Amount
  TransactionOutput : Locking-Script Size
  TransactionOutput : Locking-Script

Block -- Transaction
Block -- Block Header
Transaction -- TransactionInput
Transaction -- TransactionOutput

Full Peer: 储存完整的Block
- BlockSize
- BlockHeader
- Transaction Counter
- Transactions
SPV Client
- Block Size
- Block Header

            graph LR
            Full_Peer-->SPV_Client
SPV_Client-->Full_Peer

工作量证明

比特币参与者有两个身份
- 交易者
- 矿工
矿工从事比特币挖矿活动: 即将最近发送的交易记录在账本上
- 生成区块，并加入到链条中
矿工有一定可能性获得报酬
矿工可以随时退出，也可以随时有新的矿工加入
挖矿有一定难度，矿工之间存在竞争关系

收集交易单

每笔交易的付款人，不但要将交易单交到付款人，还要同期把交易单投递到每个矿工小组的收件箱里
矿工定期到自己收件箱里把收集到的交易单一并取出

填写账本

按笔填写交易记录
填写区块头，前一区块头Hash值，Nonce值等
Nonce值可任意填一个数字

满足条件

新区块记录的交易需要得到其他矿工的确认
新区块头的Hash必须满足计算量要求
- 矿工需要选择适合的随机数Nonce
  - H(prev_hash, Nounce, Merkle_root, 其他投币字段) $<$ E
  - E是系统规定难度，如0x00000000FFFFFFFFFFFFFFFFFFFFFFFF...

人为的制造成本

            graph LR
            矿工1-->最后一个区块
矿工2-->最后一个区块
矿工3-->最后一个区块
矿工-->最后一个区块
矿工n-->最后一个区块
最后一个区块-->区块

当其他矿工按照你的区块作为最后一个区块并开始计算时，记为认可

认证Verification非常简单，但是实现很难

考虑256bit
低于前n位是0的情况，计算出结果是完全随机的
对于n位0，需要平均算 $2^{n-1}$ 次尝试

需要维持区块生成的速度

难度值设置原则: 区块链被设计为平均每10分钟生成一个新区块
需要定期更新难度值E
- 全网均会自动统计过去2016个区块生成耗时，重新计算出下一个2016区块难度值的目标值
按10分钟一个区块生成速度，2016个区块生成时间为2016*10分钟=14天
新目标值=当前目标值*实际2016个区块出块时间/理论2016个区块出块时间

共识机制

每一个区块的交易清单第一条交易为：系统给这个矿工支付50个比特币
如果某矿工生成了一张合法的区块，并且被所有挖矿小组接受确认了，那么就意味着这条交易也被接受了，该矿工获得了50个比特币
某矿工生成了一个区块，为了得到奖励，必须立刻让其他矿工确认
系统规定当某个矿工接到其他矿工送来的新区块时，必须立刻停下手里的挖矿工作进行确认
需要确认的信息有三个
- 区块HASH满足难度值要求
- 区块的前一个区块有效
  - 前一区块确实时自己的最后一个区块，且HASH正确
- 交易清单有效
  - 如：付款人有余额

公布新区块

当新生成的区块发送出去后，如果收到新的区块，且前一个区块时自己发送出去的，则工作成功被其他人认可了
任何一个矿工当新生成有效区块或确认了别的矿工的区块，就将最新被这个矿工承认的交易写到公告牌上，收款人只要发现相关交易被哥哥矿工认可了，基本就可以认为这笔钱已经到了自己的帐上，后面它就可以在付款时将钱的来源指向这笔交易

同时收到两个合法的区块

矿工工作是并行的

它们收拾基于当前这个矿工的区块链的最后一个区块
并且区块内容都完全合法
区块头HASH满足难度值要求

不应该以线性的方式组值账本，而应该以树状组织账本，任何时刻，都以当前最长分支作为主账本，但是保留其他分支

            graph LR
            O-->A-->A1
O-->B-->B1-->B2

收款人在公告挂出时不能立即确认交易完成，而是需要等待一段时间，等到各个挖矿小组再挂出6张确认区块，并且之前的区块没有被取消，才能确认钱已到账

攻击者想要在落后6个区块的情况下从另外一个分支赶超当前主分支时非常困难的，除非攻击者拥有超过全部1/2的算力

通货膨胀

刚开始协议每生成一页账本（一个区块），奖励矿工50个比特币
每当账本增加21000页，奖励就减半
当账本达到693000页后，新生成的账本页就没有奖励了，比特币数量大约 $21000000$ 个

到时，矿工的收益会由生成的区块所得变为收取手续费，转账时可以指定1%作为手续费，矿工会挑选手续费高的交易单进行确认

防止篡改

改变区块内交易记录: Merkle根对应不上
改变区块内交易记录和Merkle根: 区块Hash对应不上
没有达到难度要求就提交了区块: 51%的人都承认这个错误就攻击失败
改变区块内容和区块Hash: 导致本区块下一个区块头内保存的prev_hash对应不上
即便掌握了51%甚至更高算力: 称为合法的良民收益会更大更安全

基于公开密钥实现身份标识，交易签名

对于每笔交易

有唯一的编号
付款人签名
前面看放在交易记录中
- 付款人私钥(当前交易+收款人的Public Key)
任何人可以验证
任何人都可有追踪交易历史

比特币交易没有找零交易

input: None
Output: 25.0 -> ALice
---
input: 1[0]
Output: 17.0 -> Bob, 8.0 -> ALice
Signed(Alice)
---
input: 2[0]
Output: 8.0 -> Carol, 9.0 -> Bob
Signed(Bob)
---
input: 2[1]
Output: 6.0 -> David, 2.0 -> ALice
Signed(Alice)

将公钥转化为钱包地址
和之前的交易输出的钱包地址做比较
- 相等: 有效
用Bob的公钥验证签名
- 证实Bob的确拥有之前交易的钱
- 本次交易时Bob发起的
- 保证了本次交易的完整性
输入的钱大于等于输出的钱

钱包地址

            graph LR
            RANDOM-->私钥-->SECP256K1-->公钥-->SHA256-->RIPEMD160-->公钥哈希

            graph LR
            公钥哈希--double-SHA256-->前4个字节
前4个字节-->公钥哈希+4位校验
公钥哈希-->公钥哈希+4位校验
公钥哈希+4位校验-->BASE58编码-->钱包地址

公钥算法时SECP256K1（基于ECC），考虑到算法强度和较短的公钥

            graph LR
            私钥 --> 公钥
公钥 --不可逆--> 私钥
公钥 --> 公钥哈希
公钥哈希 --不可逆--> 公钥
公钥哈希 --> 钱包
钱包 --> 公钥哈希

虽然每个人给公钥是匿名的，但是账本是公开的，能看到比特币拥有者的公钥，即可查出所有账本
每个公钥后面真实的人的身份都是保密的，并且可以拥有无限多的公钥

如果每一次交易用不同的公钥，这样就追查不到同一个人的所有账目了

防火墙

防火墙设计的基本目标 - 定义一个必经之点

对于一个网络来说，所有通过内部和外部的流量都要警告防火墙
通过一些策略，来保证只有经过授权的流量才可以通过防火墙
防火墙本身必须建立再安全的操作系统之上

防火墙的访问控制能力

服务器控制，确定哪些服务可以被访问
方向控制，对于特定的服务，确定运行哪个方向能够通过防火墙
用户控制，根据用户来控制对服务的访问
行为控制，控制一个特定的服务的行为

绕过防火墙的攻击是防御不了的
不能防御内部的攻击
防火墙不能防止被病毒感染的程序、文件或邮件等
防火墙有性能要求

入侵检测系统IDS

访问控制
- 在复杂的系统中，这些策略无法充分
入侵检测
- 通过计算机网络等关键点收集信息并进行分析
- 从而只能地发现网络或系统中是否有违反安全策略的行为和被攻击的迹象
  - 信息收集
  - 分析引擎
  - 相应部件

基于主机
基于网络
基于内核
基于应用

包过滤路由

对于每个进来的包，适用一组规则，然后决定转发或者丢弃该包
往往配置成双向的
过滤的规则以IP和传输层的头中的域为基础
- 包括源和目标的IP地址，IP协议域，源和目标端口，标志位
  - 标志位: SYN RST FIN ACK PSH URG
过滤器往往建议一组规则，根据IP包是否匹配规则中指定的条件来做出决定
- 如果匹配到一条规则，则根据此规则决定转发或者丢弃
- 如果所有规则否不匹配，则根据缺省策略
  - 没有被拒绝的流量都可以通过
  - 没有被允许的流量都要拒绝

Telnet服务

往外包的特征	往内包的特征
IP源是内网地址	IP源是server
目标地址为server	目标地址是内网地址
TCP协议，目标端口23	TCP协议，源端口23
源端口>1023	目标端口>1023
连接的第一个包ACK=0，其他包	所有往内的包都是ACK=1

IP地址欺骗
- 假冒内网IP地址
- 在外部接口上禁止内网地址
源路由攻击: 即由源指定路由
- 禁止这样的选项
小碎片攻击
- 丢弃分片太小的分片
利用复杂协议和配置失误进入防火墙
- 利用ftp进行内网扫描

应用层网关

代理服务器

所有连接都通过防火墙，防火墙作为网关
在应用层上实现
可以监视包的内容
可以实现基于用户的认证
所有应用需要单独实现
可以提供理想的日志功能
非常安全，但是开销比较高

有些服务要求之间连接，无法使用代理

防火墙部署

堡垒主机: 对外部网络暴露，同时也是内部网络用户的主要连接点
双宿主主机: 至少有两个网络接口的通用计算机系统
DMZ: 在内部网络和外部网络之间增加的一个子网
包过滤
- 所有的流量都哦通过堡垒主机
单宿主堡垒主机
- 只允许堡垒主机可以与外部之间通讯
- 两层保护: 包过滤+应用层网关
- 一旦包过滤路由器被攻破，则内部网络暴露
双宿主堡垒主机
- 从物理上把内部网络和Internet隔开，必须通过2层屏障
- 两层保护: 包过滤+应用层网关
屏蔽子网防火墙
- 三层防护
- 外面的router只向Internet暴露屏蔽子网中的主机
- 内部的router只向内部私有网暴露屏蔽子网中的主机

参考

信息安全——复旦大学（MOOC 优质课程）