[数理统计] - 线性回归

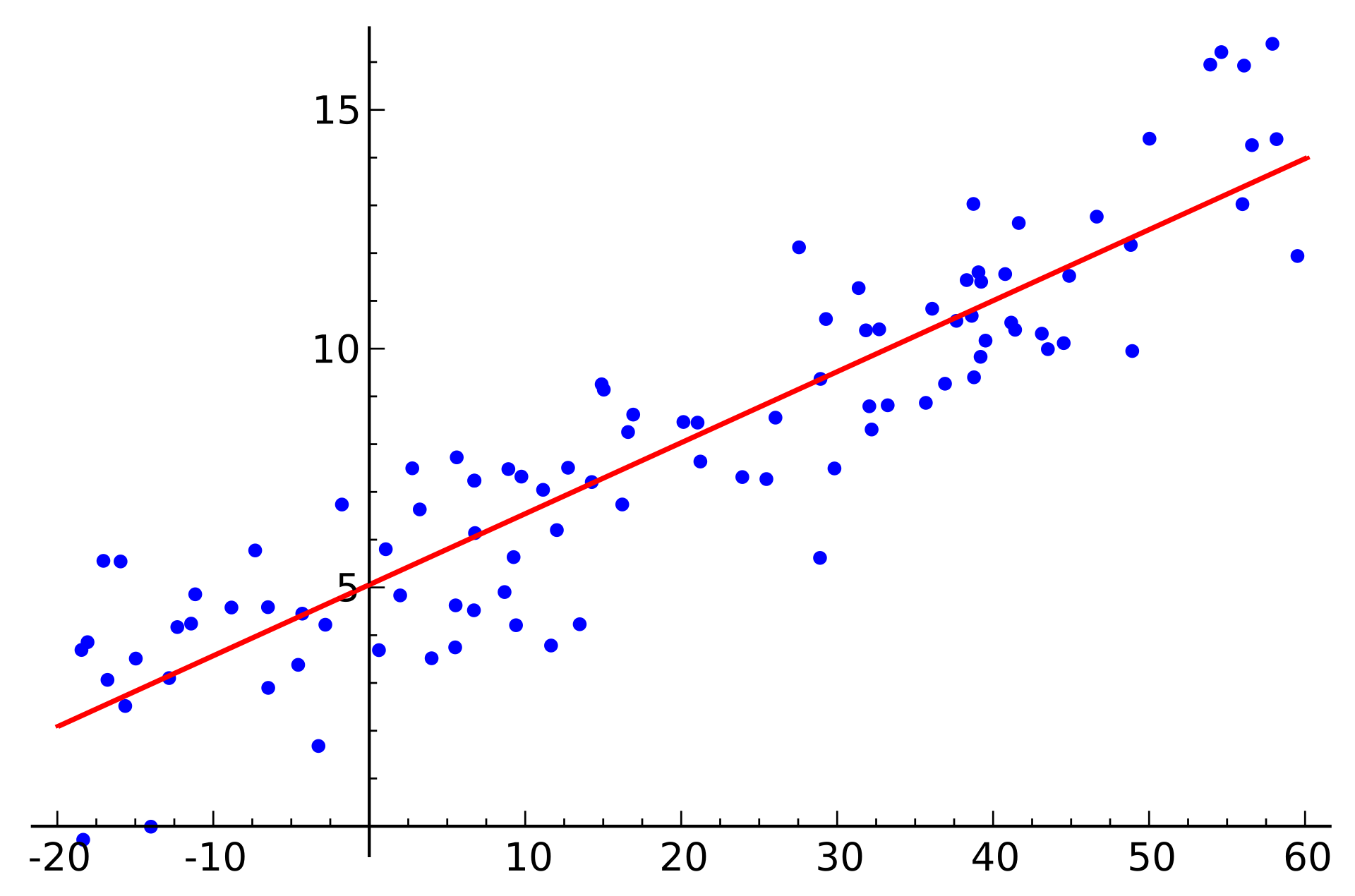
线性回归分析，可以通过一个已知的变量的值，进而推断一个未知的变量的确切的值。

我们对于$x$取定一组不完全相同的值$x_1, x_2, \cdots, x_n$，设$Y_1, Y_2, \cdots, Y_n$分别是在$x_1, x_2, \cdots, x_n$处对$Y$的独立观察结果，称

$(x_1, Y_1), (x_2, Y_2), \cdots, (x_n, Y_n)$

是一个样本，对应的样本值记为

$(x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)$

一元线性回归

假设对于$x$（在某个区间内）的每一个值有

$Y \sim N(a + bx, \sigma^2)$

其中$a,b$及$\sigma^2$都是不依赖于$x$的未知参数，记$\varepsilon = Y - (a + bx)$，对$Y$作这样的正态假设，即

$Y = a + bx + \varepsilon, \quad \varepsilon \sim N(o, \sigma^2)$

其中未知参数$a, b$及$\sigma^2$都是不依赖于$x$的未知参数，上式称为一元线性回归模型，其中$b$称为回归系数

a，b的估计

取$x$的$n$个不全相同的值$x_1, x_2, \cdots, x_n$作独立实验，得到样本

$(x_1, Y_1), (x_2, Y_2), \cdots, (x_n, Y_n)$

由一元线性回归模型得到

$Y_i = a + bx_i + \varepsilon_i, \quad \varepsilon_i \sim N(o, \sigma^2).\text{各}\varepsilon_i\text{相互独立}$

于是得到$Y_i \sim N(a + bx_i, \sigma^2), i = 1, 2, \cdots, n$，由$Y_1, Y_2, \cdots, Y_n$的独立性，知道$Y_1, Y_2, \cdots, Y_n$的联合分布为

$\begin{aligned} L &= \prod^n_{i=1}\frac{1}{\sigma \sqrt{2\pi}} \exp \Big[ -\frac{1}{2\sigma^2}(y_i - a -bx_i) \Big] \\ &= (\frac{1}{\sigma \sqrt{2\pi}})^n \exp \Big[ -\frac{1}{2\sigma^2}\sum^n_{i=1}(y_i - a -bx_i) \Big] \end{aligned}$

利用最大似然估计法来估计未知参数$a,b$，对于任意一组观察值$y_1, y_2, \cdots, y_n$上式就是样本的似然函数，只要$L$取最大值，即右式方括号中的平方和最小，即

$\min \quad Q(a,b) = \sum^n_{i=1}(y_i - a -bx_i)^2$

取$Q$分布关于$a,b$的偏导数，令它们等于$0$

$\begin{cases} \frac{\partial Q}{\partial a} &= -2 \sum^n_{i=1} (y_i - a - bx_i) = 0 \\ \frac{\partial Q}{\partial b} &= -2 \sum^n_{i=1} (y_i - a - bx_i)x_i = 0 \end{cases}$

得到方程组

$\begin{cases} na + (\sum^n_{i=1}x_i)b = \sum^n_{i=1}y_i \\ (\sum^n_{i=1}x_i)a + (\sum^n_{i=1}x^2_i)b = \sum^n_{i=1}x_iy_i \end{cases}$

称上式为正规方程组，上述线性方程的行列式

$\begin{vmatrix} n & \sum^n_{i=1}x_i \\ \sum^n_{i=1}x_i & \sum^n_{i=1}x^2_i \end{vmatrix} = n\sum^n_{i=1}x^2_i - (\sum^n_{i=1}x_i)^2 = n\sum^n_{i=1}(x_i - \overline{x})^2 \neq 0$

故方程式由唯一的解，解得$a,b$的最大似然估计值为

$\begin{aligned} \hat{b} &= \frac{n\sum^n_{i=1}x_iy_i - (\sum^n_{i=1}x_i)(\sum^n_{i=1}y_i)}{n\sum^n_{i=1}x^2_i - (\sum^n_{i=1}x_i)^2} \\ &= \frac{\sum^n_{i=1}(x_i - \overline{x})(y_i - \overline{y})}{\sum^n_{i=1}(x_i - \overline{x})^2} \\ \\ \hat{a} &= \frac{1}{n}\sum^n_{i=1}y_i - \frac{\hat{b}}{n} \sum^n_{i=1}x_i = \overline{y} - \hat{b}\overline{x} \end{aligned}$

于是对于给定的$x$，取$\hat{a} + \hat{b}x$作为回归函数$\mu(x) = a + bx$的估计，则

$\hat{y} = \hat{a} + \hat{b}x$

称为$Y$关于$x$的经验回归方程，简称回归方程，其图形称为回归直线

回归方程的简化表示

引入下述记号

$\begin{aligned} S_{xx} &= \sum^n_{i=1}(x_i - \overline{x})^2 \\ S_{yy} &= \sum^n_{i=1}(y_i - \overline{y})^2 \\ S_{xy} &= \sum^n_{i=1}(x_i - \overline{x})(y_i - \overline{y}) \end{aligned}$

$a,b$的估计值可以写作

$\begin{aligned} \hat{b} &= \frac{S_{xy}}{S_{xx}} \\ \hat{a} &= \frac{1}{n}\sum^n_{i=1}y_i - (\frac{1}{n}\sum^n_{i=1}x_i)\hat{b} \end{aligned}$

回归拟合优度

变量$y$的取值是不同的，其原因有2各方面

• 自变量$x$的取值不同
• 除$x$以外的其他因素

离差

离差的大小可以用实际观测值$y$与均值$\overline{y}$的差$y - \overline{y}$来表示，其性质

• $\sum^n_{i=1} (y_i - \overline{y}) = 0$
• $\sum^n_{i=1} x_i(y_i - \overline{y}) = 0$，即自变量$x_i$与残差直接没有关系

对于$n$次观察值的总离差，则可以用离差的平方和来表示，称为总平方和，也叫总变差，记为SST，即

$SST = \sum^n_{i=1}(y_i - \overline{y})^2$

残差

残差的大小可以用实际观测值$y$与理论值$\hat{y}$的差$e = y - \hat{y}$来表示，其性质

• $E(e) = 0$
• $Cov(e, \hat{b}) = 0$
• $D(e) = \sigma^2(I - H)$

对于$n$次观察值的残差，则可以用残差的平方和来表示，称为残差平方和，记为SSE，即

$SSE = \sum^n_{i=1}(y_i - \hat{y}_i)^2$

由上图，可以得出

$\begin{gathered} y - \overline{y} = (\hat{y} - \overline{y}) + (y - \hat{y}) \\ \Downarrow \\ \sum^n_{i=1}(y_i - \overline{y})^2 = \sum^n_{i=1}(\hat{y}_i - \overline{y})^2 + \sum^n_{i=1}(y_i - \hat{y}_i)^2 + 2\sum^n_{i=1}(\hat{y}_i - \overline{y})(y_i - \hat{y}_i) \end{gathered}$

其中$2\sum^n_{i=1}(\hat{y}_i - \overline{y})(y_i - \hat{y}_i)= 0$，即可得出

$\begin{aligned} \sum^n_{i=1}(y_i - \overline{y})^2 &= \sum^n_{i=1}(\hat{y}_i - \overline{y})^2 + \sum^n_{i=1}(y_i - \hat{y}_i)^2 \end{aligned}$

也就是

$\begin{aligned} \text{总平方和（SST）} &= \text{回归平方和（SSR）} + \text{残差平方和（SSE）} \end{aligned}$

决定系数

可以从图中看出，如果回归直线拟合较好，那么残差平方和（SSE）应该是比较低的，定义以下变量为决定系数或判定系数（coefficient of determination）

$\begin{aligned} R^2 &= \frac{\text{回归平方和}SSR}{\text{\ \ \ \ 总平方和}SST} = 1 - \frac{\text{残差平方和}SSE}{\text{\ \ \ \ 总平方和}SST} \\ &= \frac{\sum^n_{i=1}(\hat{y}_i - \overline{y})^2}{\sum^n_{i=1}(y_i - \overline{y})^2} = 1 - \frac{\sum^n_{i=1}(y_i - \hat{y}_i)^2}{\sum^n_{i=1}(y_i - \overline{y})^2} \end{aligned}$

• 如果所有观测点都落在直线上，拟合是完全的，则$R^2 = 1$
• 如果$y$的变换与$x$无关，此时$\hat{y} = \overline{y}$，则$R^2 = 0$

SSE代表了$x$不能解释的一部分变动，它越小说明模拟拟合的越好

经调整决定系数

决定系数会随着自变量的增多，趋近于$1$，为了修正这一点，引入经调整决定系数（Adjusted coefficient of determination）

$R^2_f = 1 - \dfrac{\frac{\sum^n_{i=1}(y_i - \hat{y}_i)^2}{n - k - 1}}{\frac{\sum^n_{i=1}(y_i - \overline{y})^2}{n - 1}}$

• 比较自变量数不同的回归模型的时候，使用调整决定系数
• 决定系数或调整决定系数越高，说明回归直线拟合越好

方差的估计

由

$Y = a + bx + \varepsilon, \quad \varepsilon \sim N(o, \sigma^2)$

得到

$E[(Y - (a + bx))^2] = E[\varepsilon^2] = D(\varepsilon) + E(\varepsilon)^2 = \sigma^2$

其表示$\sigma^2$越小，回归函数$\mu(x) = a + bx$作为$Y$的近似导致的均方差误差就越小。这样利用回归函数$\mu(x) = a + bx$去研究随机变量$Y$与$x$的关系就越有效，不过一般情况下$\sigma^2$是未知的，所以我们需要从样本取估计$\sigma^2$

---

记$x_i$处的残差$y_i - \hat{y}_i$为

$\hat{y}_i = \hat{y}|_{x = x_i} = \hat{a} + \hat{b}x_i$

则残差平方和为

$\begin{aligned} Q_e &= \sum^n_{i=1}(y_i - \hat{y}_i)^2 \\ &= \sum^n_{i=1}(y_i - \hat{a} - \hat{b}x_i)^2 \end{aligned}$

对$Q_e$做如下分解

$\begin{aligned} Q_e &= \sum^n_{i=1}(y_i - \hat{y}_i)^2 \\ &= \sum^n_{i=1}(y_i - \overline{y} - \hat{b}(x_i - \overline{x}))^2 \\ &= \sum^n_{i=1}(y_i - \overline{y})^2 - 2\hat{b}\sum^n_{i=1}(x_i - \overline{x})(y_i - \overline{y}) + \hat{b}^2\sum^n_{i=1}(x - \overline{x})^2 \\ &= S_{yy} - 2\hat{b}S_{xy} + \hat{b}^2S_{xx} \end{aligned}$

其中$\hat{b} = S_{xy}/S_{xx}$，化简得到$Q_e$的一个分解式

$Q_e = S_{yy} - \hat{b}S_{xy}$

对于上式的残差平方和的统计量$Q_e$，我们先令$y = Y$

$\begin{aligned} S_{YY} &= \sum^n_{i=1}(Y_i - \overline{Y})^2 \\ S_{xY} &= \sum^n_{i=1}(x_i - \overline{x})(Y_i - \overline{Y}) \end{aligned}$

则统计量$Q_e$为

$Q_e = S_{YY} - \hat{b}S_{xY}$

其服从$\chi^2(n -2)$分布

$\frac{Q_e}{\sigma^2} \sim \chi^2(n -2)$

可以得到期望

$E(\frac{Q_e}{\sigma^2}) = n - 2$

于是从$E(\frac{Q_e}{n-2}) = \sigma^2$，就得到$\sigma^2$的无偏估计量

$\hat{\sigma}^2 = \frac{Q_e}{n-2} = \frac{1}{n-2}(S_{YY} - \hat{b}S_{xY})$

线性假设的显著性检验

我们都是假定$Y$关于$x$的回归$\mu(x)$具有$a+b$形式，但是我们无法断定$\mu(x)$是否为$x$的线性函数，一般需要通过假定检验才能确定，若$Y = a + bx + \varepsilon$满足实际，则$b$不应为$0$，若$b = 0$，则$E(Y) = \mu(x)$不依赖于$x$，因此检验假设

$\begin{aligned} H_0: \quad b = 0 \\ H_1: \quad b \neq 0 \end{aligned}$

利用$t$检验法，我们可以知道

$\hat{b} \sim N(b, \frac{\sigma^2}{S_{xx}})$

由

$\begin{cases} \frac{Q_e}{\sigma^2} \sim \chi^2(n -2) \\ \hat{\sigma}^2 = \frac{Q_e}{n-2} = \frac{1}{n-2}(S_{YY} - \hat{b}S_{xY}) \end{cases}\Rightarrow \frac{(n - 2)\hat{\sigma}^2}{\sigma^2} = \frac{Q_e}{\sigma^2} \sim \chi^2(n - 2)$

且$\hat{b}$与$Q_e$独立，可以得到

$\frac{\frac{\hat{b} - b}{\sqrt{\frac{\sigma^2}{S_{xx}}}}}{\sqrt{\frac{\frac{(n - 2)\hat{\sigma}^2}{\sigma}}{n - 2}}} \sim t(n - 2)$

也就是

$\frac{\hat{b} - b}{\hat{\sigma}} \sqrt{S_{xx}} \sim t(n - 2), \quad \hat{\sigma} = \sqrt{\hat{\sigma}^2}$

当$H_0$为真的时候，$b = 0$，此时统计量$t$的值为

$t = \frac{\hat{b}}{\hat{\sigma}}\sqrt{S_{xx}} \sim t(n - 2)$

且$E(\hat{b}) = b = 0$，即得到$H_0$的拒绝域为

$|t| = \frac{|\hat{b}|}{\hat{\sigma}}\sqrt{S_{xx}} \geq t_{a/2}(n - 2)$

当假设$H_0: b = 0$被拒绝时，也就是系数不为$0$，认为回归效果时显著的，反之，认为回归效果不显著，其原因可能为

• 影响$Y$取值的，除$x$及随机误差外还有其他不可忽略的因素
• $E(Y)$与$x$的关系不是线性的，而存在其他的关系
• $Y$与$x$不存在关系

在实际中，我们还可能使用$t$的值计算出P-值（$Pr(>|t|)$），然后再进行检定

系数b的置信区间

当回归效果显著时，可能需要对系数$b$作区间估计，由$\frac{\hat{b} - b}{\hat{\sigma}} \sqrt{S_{xx}} \sim t(n - 2)$得到$b$的置信水平为$1 - a$的置信水平为$1 - a$的置信区间为

$(\hat{b} \pm t_{a/2}(n - 2) \times \frac{\hat{\sigma}}{\sqrt{S_{xx}}})$

可化为一元线性回归的例子

$Y = ae^{\beta x} \cdot \varepsilon, \quad \ln \varepsilon \sim N(0,\sigma^2)$

其中$a, \beta, \sigma^2$是与$x$无关的未知参数，两边取对数得到

$\ln Y = \ln a + \beta x + \ln \varepsilon$

令$\ln Y = Y', \ln a = a, \beta = b, x = x', \ln \varepsilon = \varepsilon'$，则

$Y' = a + bx' + \varepsilon', \quad \varepsilon' \sim N(0, \sigma^2)$

---

$Y = ax^\beta \cdot \varepsilon, \quad \ln \varepsilon \sim N(0, \sigma^2)$

其中$a, \beta, \sigma^2$是与$x$无关的未知参数，两边取对数得到

$\ln Y = \ln a + \beta \ln x + \ln \varepsilon$

令$\ln Y = Y', \ln a = a, \beta = b, \ln x = x', \ln \varepsilon = \varepsilon'$，则

$Y' = a + bx' + \varepsilon', \quad \varepsilon' \sim N(0, \sigma^2)$

---

$Y = a + \beta h(x) + \varepsilon, \quad \varepsilon \sim N(0,\sigma^2)$

其中$a, \beta, \sigma^2$是与$x$无关的未知参数，$h(x)$是$x$的已知函数，
令$a = a, \beta = b, h(x) = x'$，则

$Y = a + bx' + \varepsilon, \quad \varepsilon' \sim N(0, \sigma^2)$

上述得到$Y$关于$x'$的回归方程后，再将原自变量$x$代回，就得到$y$关于$x$的回归方程，它的图形是一条曲线，也称为曲线回归方程

回归分析表

假设回归模型为(R语言)

$y = a + \beta_1 \times R_1 + \beta_2 \times \log(R_2) + \text{残差}$

Coefficients:
              Estimate    Std. Error      t value       Pr(>|t|)
(Intercept)  -1.283e+03    1.137e+02      -11.278       1.39e-15
population   -6.617e-02    1.046e-02       -6.326       5.87e-08
log(gdp)      1.757e+02    1.175e+01       14.959        < 2e-16
---

Residual standard error: 103.5 on 52 degrees of freedom
Multiple R-squared: 0.821      Adjusted R-squared: 0.8141
F-statistic: 119.2 on 2 and 52 DF,     p-value: < 2.2e-16

翻译过来即

计算结果:
                参数估计列    参数的标准差      t value       Pr(>|t|)
(参数a的估计值)   -1.283e+03    1.137e+02      -11.278       1.39e-15
population      -6.617e-02    1.046e-02       -6.326       5.87e-08
log(gdp)         1.757e+02    1.175e+01       14.959        < 2e-16
---

残差的标准差: 103.5 on 自由度: 52
决定系数: 0.821      经调整决定系数: 0.8141
F统计量: 119.2  自由度: (2, 52),     p值: < 2.2e-16

• Coefficients：表示参数估计的计算结果。
• Estimate：为参数估计列。Intercept行表示常数参数a的估计值 ，x行表示自变量x的参数b的估计值。
• Std. Error：为参数的标准差，sd(a), sd(b)
• t value：为t值，为T检验的值
• Pr(>|t|)：表示P-value值，用于T检验判定，匹配显著性标记
• Residual standard error：表示残差的标准差，自由度为n-2
• Multiple R-squared：为相关系数$R^2$的检验，越接近1则越显著。
• Adjusted R-squared：为相关系数的修正系数，解决多元回归自变量越多，判定系数$R^2$越大的问题
• F-statistic：表示F统计量，自由度为$(1, n-2)$
• p-value：用于F检验判定，匹配显著性标记

Pr(>|t|)如果小于$0.05$，那么我们就有95%的信心相信，这个自变量的系数不是0，也就是原假设不成立。

多元线性回归

实际问题中，随机变量$Y$可能与多个普通变量$x_1, x_2, \cdots, x_p,(p > 1)$有关，对于自变量$x_1, x_2, \cdots, x_p$的一组确定的值，$Y$有他的分布，若$Y$的数学期望存在，则它是$x_1, x_2, \cdots, x_p$的函数，这里研究的是$\mu(x_1, x_2, \cdots, x_p)$是$x_1, x_2, \cdots, x_p$的线性函数的情况，即

$Y = b_0 + b_1x_1 + \cdots b_px_p + \varepsilon, \quad \varepsilon \sim N(0, \sigma^2)$

其中$b_0, b_2, \cdots, b_p, \sigma^2$都是$x_1, x_2, \cdots, x_p$无关的未知参数，设

$\begin{aligned} (x_{11}, x_{12}, &\cdots, x_{1p}, y_1) \\ (x_{21}, x_{22}, &\cdots, x_{2p}, y_2) \\ &\vdots \\ (x_{n1}, x_{n2}, &\cdots, x_{np}, y_n) \end{aligned}$

是一个样本，类似一元线性回归的情况，采用最大似然估计法来估计参数，取$\hat{b}_0, \hat{b}_1, \cdots, \hat{b}_p$，使当$b_0 = \hat{b}_0, b_1 = \hat{b}_1, \cdots, b_p = \hat{b}_p$时

$Q = \sum^n_{i=1}(y_i - b_0 - b_1x_{i1} - b_2x_{i2} - \cdots - b_px_{ip})^2$

达到最小，对$Q$求分别关于$b_0, b_2, \cdots, b_p$的偏导数，并令它们等于零，得到

$\begin{aligned} \frac{\partial Q}{\partial b_0} &= -2 \sum^n_{i=1}(y_i - b_0 - b_1x_{i1} - \cdots - b_px_{ip}) = 0 \\ \frac{\partial Q}{\partial b_j} &= -2 \sum^n_{i=1}(y_i - b_0 - b_1x_{i1} - \cdots - b_px_{ip})x_{ij} = 0, \quad j = 1,2,\cdots,p \end{aligned}$

化简后得到

$\begin{aligned} b_0 n + b_1\sum^n_{i=1}x_{i1} + b_2\sum^n_{i=1}x_{i2} + \cdots + b_p\sum^n_{i=1}x_{ip} &= \sum^n_{i=1}y_i \\ \\ b_0\sum^n_{i=1}x_{i1} + b_1\sum^n_{i=1}x_{i1} + b_2\sum^n_{i=1}x_{i1}x_{i2} + \cdots + b_p\sum^n_{i=1}x_{i1}x_{ip} &= \sum^n_{i=1}x_{i1}y_i \\ \vdots \\ b_0\sum^n_{i=1}x_{ip} + b_1\sum^n_{i=1}x_{ip} + b_2\sum^n_{i=1}x_{ip}x_{i2} + \cdots + b_p\sum^n_{i=1}x_{ip}x_{ip} &= \sum^n_{i=1}x_{ip}y_i \end{aligned}$

上式称为正规方程组，为了更方便的表达，将上式写作矩阵的形式

$X = \begin{pmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1p} \\ 1 & x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \vdots & \ddots &\vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{np} \end{pmatrix}, \quad Y = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}, \quad B = \begin{pmatrix} b_0 \\ b_1 \\ \vdots \\ b_p \end{pmatrix}$

即可化简为

$X^TXB = X^TY$

即为正规方程式的矩阵形式，若$X^TX$可逆，则可以得到

$\hat{B} = \begin{pmatrix} \hat{b}_0 \\ \hat{b}_1 \\ \vdots \\ \hat{b}_p \end{pmatrix} = (X^TX)^{-1}X^TY$

即为$(b_0,b_1,\cdots,b_p)^T$的最大似然估计，取

$\hat{b}_0 + \hat{b}_1x_1 + \cdots + \hat{b}_px_p$

作为$\mu(x_1, x_2, \cdots, x_n)$的估计，方程

$\hat{y} = \hat{b}_0 + \hat{b}_1x_1 + \cdots + \hat{b}_px_p$

称为$p$元经验线性回归方程，简称回归方程

多元线性假设的显著性检验

类似一元线性回归，多元线性假设的显著性检验需要检验假设

$\begin{aligned} H_0&: \quad b_1 = b_2 = \cdots = b_p = 0 \\ H_1&: \quad b_i \neq 0, \quad i =1,2,\cdots,p \end{aligned}$

总结

在实际问题中，与$Y$有关的因素可能有很多，有些自变量对$Y$的影响很小，删除后可以使回归方程变得简洁，易于应用，且能明确哪些因素的改变对$Y$由显著的影响，需要按照情况具体分析