最优化问题
最优化问题的数学模型一般形式为
mins.t.f0(x)fi(x)=0,fi(x)≥0i=1,⋯,mi=m+1,⋯,p
无约束最优化问题:无任何约束的最优化问题
minf(x),x∈Rn
约束最优化问题:只要问题中存在任何约束条件,就称为约束最优化问题
等式约束问题:只有等式的约束的情况
mins.t.f(x)fi(x)=0,i=1,⋯,m
不等式约束问题:只有不等式的约束的情况
mins.t.f(x)fi(x)≥0,i=1,⋯,m
二次规划问题:所有约束都是x的线性函数的时候
mins.t.f(x)=21xTGx+cTx+dAix=b1A2x≥b2
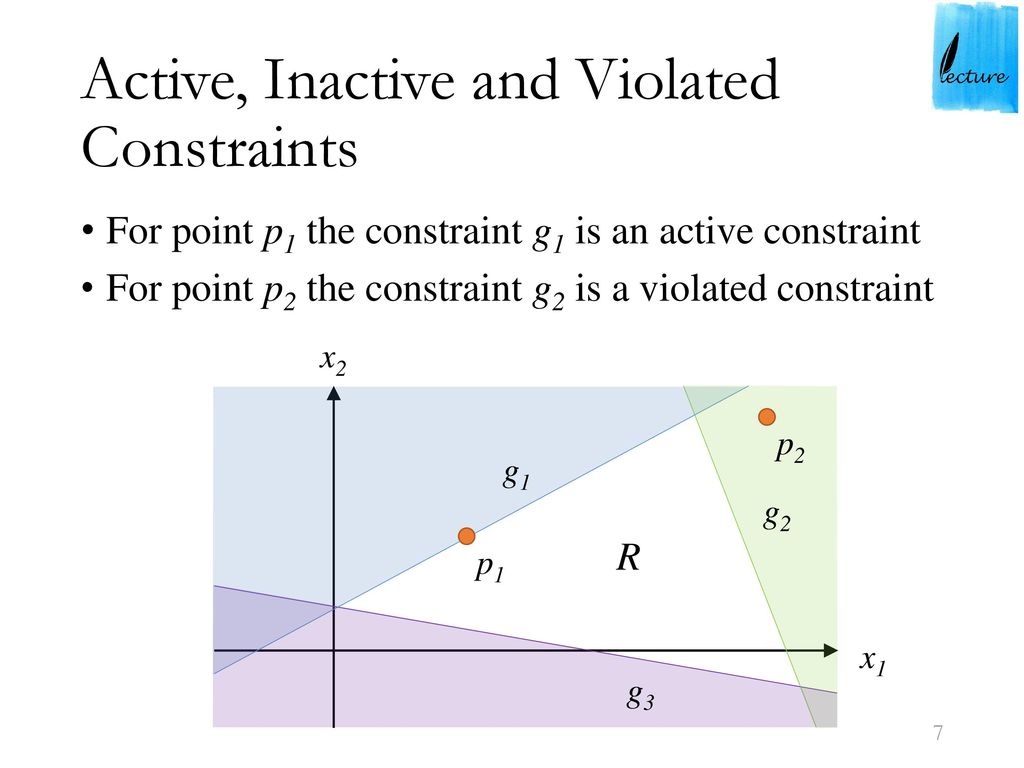
可行点:点满足最优化模型中所有约束条件
可行域:所有可行点的全体
- 最优化问题一般很难解决
- 一般解决方法多少有一些妥协
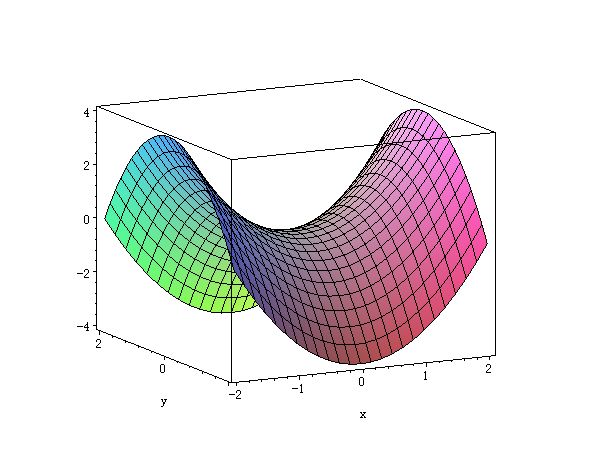
凸优化问题
mins.t.f0(x)fi(x)<0,aiTx=bi,i=1,⋯,mi=1,⋯,p
上述优化问题中,fi(x)是凸函数,此类问题称为凸优化问题
对比优化文图:目标函数和不等式约束为凸函数,等式约束时仿射函数的优化问题属于凸优化问题。
- 凸优化的最优解集是凸集
- 凸优化的局部最优解都是全局最优解
优化问题隐式约束
x∈D=i=0⋂mfi∩i=2⋂pdomhi
- D:问题的定义域,定义域外返回:+∞
- fi(x)≤0,hi(x)=0是显性约束条件
- 问题是有约束,如果没有显性约束条件(m=p=0)
相同的优化问题
2个问题可以是等价的,如果其中一个解能轻易的从另外一个问题中获得
例子
mins.t.f0(x)fi(x)<0,aiTx=bi,i=1,⋯,mi=1,⋯,p
和
mins.t.f0(Fz+x0)fi(Fz+x0)<0,i=1,⋯,m
是等价的,其中F,x0对于一些z满足
mins.t.f0(A0x+b0)fi(Aix+b0)<0,i=1,⋯,m
等价于
mins.t.f0(y0)fi(yi)<0,yi=Aix+bi,i=1,⋯,mi=1,⋯,m
优化问题基本概念
- 凸集:定义目标函数和约束函数的定义域。
- 凸函数:定义优化相关函数的凸性限制。
- 凸优化:中心内容的标准描述。
- 凸优化问题求解:核心内容。相关算法,梯度下降法、牛顿法、内点法等。
- 对偶问题:将一般优化问题转化为凸优化问题的有效手段,求解凸优化问题的有效方法。
convexity means non-negative curvature, it means it curves up.
超平面
设D1,D2为两个非空凸集,若存在a=0,∀β∈R,使得
H={x∈Rn ∣ aTx=β}
分离了集合D1和D2,称H为超平面
∀d∈D1→aTd≥β∀d∈D2→aTd≤β
- 二维分割需要一条线,三维分割需要一个面,所以N维分割需要N−1维的超平面
- 超平面可以表示为aTx=β
多面体
多面体被定义为有限个线性等式和不等式的解集
P={x ∣ aTx≤bj,j=1,2,⋅,m,cjT=dj,j=1,2,⋅,p}
- 几何上来看,多面体是有限个半空间和超平面的交集
- 多面体是凸集,有界多面体也成为多胞形,表示为P={x ∣ Ax≤b,Cx=d}
- 以下几何都是多面体
向量不等式
符号:⪯,>
代表Rm上的向量不等式或分量不等式
uui≤vi,⪯v表示1=1,2,⋯,m
广义不等式
称锥K⊆Rn为正常锥,如果它满足下列条件
- K是凸的
- K是闭的
- K是实的,即具有非空内部
- K是尖的,即不包含直线(x∈K,−x∈K⇒x=0)
正常锥K可以用来定义广义不等式,即Rn上的偏序关系
x⪯Ky⇔y−x
单纯形
单纯体是一类多面体,设k+1个点v0,⋅,vk∈Rn仿射独立,即
v1−v0,⋅,vk−v0
线性独立,则这些点决定了一个单纯形
C=conv{v0,⋅,vk}={θ0v0,⋅,θ0vk ∣ θ>0,1Tθ=1}
- 其中1表示所有分量均为1的向量
- 这个单纯形的仿射维数为k,称为Rn空间的k维单纯形
- 常见单纯性
- 1维单纯形:一条线段
- 2维单纯形:一个三角形
- 3维单纯形:一个四面体
锥
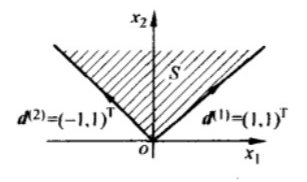
对于任意x∈C和θ≥0都有θx∈C,我们称集合C是锥或者非负齐次。
如果集合C是锥,并且是凸的,则称C为凸锥,即对∀x1,x2∈C和θ1,θ2≥0,都有
θ1x1+θ2x2∈C
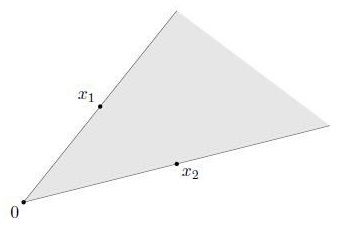
在几何上,具有此类形式的点构成了二维的扇形,这个扇形以0为顶点,边通过x1和x2

半正定锥
用Sn表示对称n×n矩阵的集合,即
S+n={X∈Rn×n∣X=XT}
这是一个维数为n(n+1)/2的向量空间,我们用S+n表示对称半正定矩阵的集合
S+n={X∈Sn∣X>0}
用S++n表示对称正定矩阵的集合
S++n={X∈Sn∣X≻0}
- R+:表示非负实数
- R++:表示正实数
极点
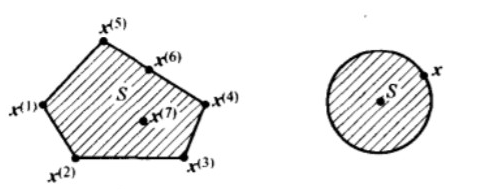
设S为非空集合,x∈S,若x不能表示成S中两个不同点的凸组合,即
x=λx1+(1−λ)x2,λ∈(0,1).x1,x2∈S
则必有x=x1=x2,则称x是凸集S的极点

极方向
设S为Rn中的闭凸集,d为非零向量,如果对S中的每一个x,都有射线
{x+λd ∣ λ≤0}⊂S
则称向量d为S的方向,又设d1,d2为S的两个反向,若对任意整数λ,有d1=λd2,则称d1,d2是两个不同的方向,若S的方向d不能表示成集合的两个不同方向的正的线性组合,则称d为S的极方向

有界集不存在方向,也不存在极方向,无界集才有方向的概念
凸集
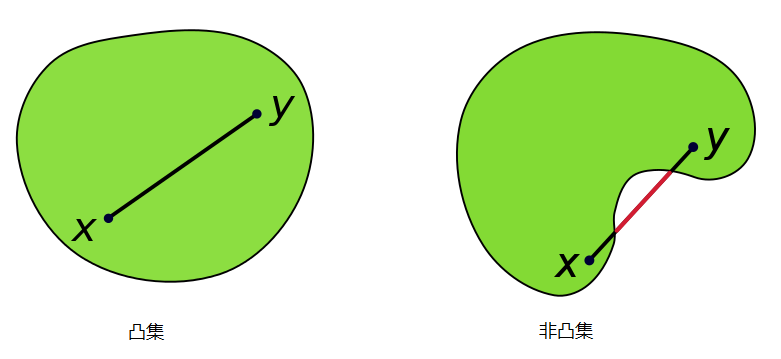
凸集(convex set)是一个点集合,其中每两点之间的直线点都落在该点集合中。

设S∈Rn(实或复向量空间的集), 若对于所有x,y∈S,和所有λ∈[0,1]存在λx+(1−λ)y∈S,则S是凸集,其中λx+(1−λ)y称作点x,y之间的凸连接
例子:
设A∈Rm×n,b∈Rn,证明S={x∈Rn∣Ax=b,x≥0}是凸集。
证明流程:
{x,y∈Sλ∈[0,1]⇔(Ax=b,x≥0Ay=b,y≥0)
w=λx+(1−λ)y∈S⇔(Aw=b,w≥0)
典型的凸集
- 线段,射线,直线
- 超平面,半空间
- 仿射集
- 欧几里得球,范数球,椭球等
- 凸锥,范数锥等
凸函数
函数f:Rn→R定义域domf是凸集,且对于∀x,y∈domf和∀θ,0≤θ≤1有
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
则称函数f是凸函数

凸函数与凸集合的关系:
下水平集:函数f的下水平集Ca={x∈domf ∣ f(x)≤a}是其定义域的子集,凸函数的下水平集是凸集
上镜图:函数f:Rn→R的上镜图epif={(x,t) ∣ x∈domf,f(x)≤t},他是Rn+1空间的子集。
狭义凸函数
f(θx+(1−θ)y)<θf(x)+(1−θ)f(y)
凸函数与凸集合的关系
定理:如果S是Rn中的一个凸集,f是定义在S上的凸函数,则f在S内部连续
凸函数与凸集的关系:一个函数是凸函数,当且仅当其上镜图是凸集
典型凸函数
- 线性函数和仿射函数:f(x)=aTx+b
- 指数函数
- 负熵
- 范数:∥x∥p
设f,g:Rn→R是凸函数,λ>0
- f+g
- λf
- max(f,g)
都是凸函数
| 函数 |
式子 |
∇f(x) |
∇2f(x) |
| 二次型 |
f(x)=21xTPx+qTx+r |
∇f(x)=Px+q |
∇2f(x)=P |
| 最小二乘 |
f(x)=∥Ax−b∥22 |
∇f(x)=2AT(Ax−b) |
∇2f(x)=2ATA |
凸函数性质
凸函数的重要特性:任意局部最优解也是全局最优解
设f:Rn→R
x∗全局的最小解:f(x∗)≤f(x),∀x∈Rn
x∗局部的最小解:∃ε>0,f(x∗)≤f(x),∀x→∣x∗−x∣<ε
一般来说:找到局部的最小解即可
一阶条件
可微函数f是凸函数的充要条件是
- 定义域domf是凸集
- 对于∀x,y∈R有
[∇f(x)−∇f(y)]T(x−y)≥0
- 对于∀x,y∈domf有
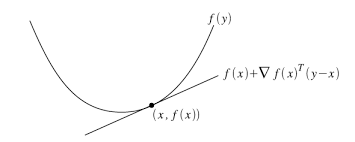
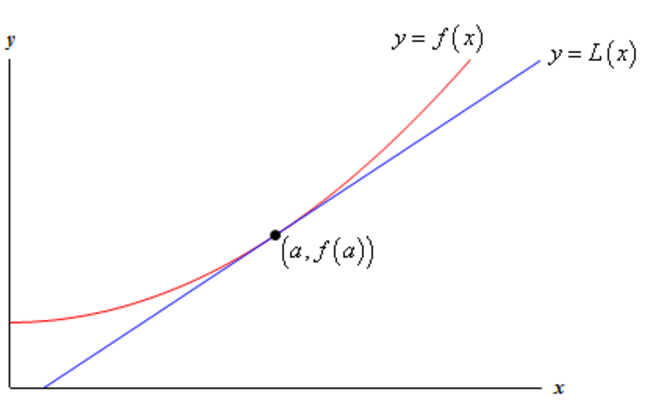
f(y)≥f(x)+∇f(x)T(y−x)
f(x)+∇f(x)T(y−x)即函数f(y)在点x附近的Taylor近似。对于一个凸函数

- 其一阶Taylor近似实质上是原函数的一个全局下估计
- 某函数的一阶Taylor近似总是全局下估计,则这个函数是凸的
简单的来说:对于函数在定义域的任意取值,函数的值都大于或等于对这个函数在这一点的一阶近似
二阶条件
函数f的二阶偏导函数称为函数f的Hessian矩阵(黑塞矩阵)
对于函数f定义域domf内任意一点,其Hessian矩阵存在,则函数f是凸函数的充要条件是
∀x∈domf→∇2f(x)>0
同理可以等价于:
- Hessian矩阵是半正定矩
- 对于R上的函数,可以简化为f′′(x)≥0(f导函数非减)
- 从几何上理解就是函数图像在点x处有正(向上)的曲率
保凸运算
非负加权求和
如果函数f1和f2都是凸函数,则f1+f2也是凸函数
复合仿射映射
假设函数f:Rn→R,A∈Rn×m,以及b∈Rn,定义g:Rm→R为
g(x)=f(Ax+b)
其中domg={x ∣ Ax+b∈domf}
- 若函数f是凸函数,则函数g是凸函数
- 若函数f是凹函数,则函数g是凹函数
逐点最小和逐点下确界
如果函数f1和f2均为凸函数,则二者的逐点最小函数f
f(x)=min(f1(x),f2(x))
其定义域为domf=domf1∩domf2,仍然时凸函数
证明:
∀θ∈[0,1],x,y∈domf,则
f(θx+(1−θ)y)=min(f1(θx+(1−θ)y),f2(θx+(1−θ)y))≤min(θf1(x)+(1−θ)f1(y),θf2(x)+(1−θ)f2(y))≤θmin(f1(x),f2(x))+(1−θ)min(f1(y),f2(y))=θf(x)+(1−θ)f(y)
同理,可得出
f(x)=min(f1(x),f2(x),⋯,fm(x))
仍然是凸函数
铸点最大的性质可以扩展至无限个凸函数的逐点下确界。如果对于任意y∈A,函数f(x,y)关于x都是凸的,则函数g
g(x)=y∈Ainff(x,y)
关于x也是凸函数,定义域为
domg={x ∣ (x,y)∈domf∀y∈A,y∈Ainff(x,y)<∞}
inf:最大下界
- ∀s∈S⇒s≥inf(S)
证明:
f(θx1+(1−θ)x2)=inff(θx1+(1−θ)x2,y)≤f(θx1+(1−θ)x2,θy1+(1−θ)y2)≤θf(x1,y1)+(1−θ)f(x2,y2)=θg(x1)+(1−θ)g(x2)+ϵ
对∀ϵ成立,于是
f(θx1+(1−θ)x2)=θg(x1)+(1−θ)g(x2)
逐点最大和逐点上确界
如果函数f1和f2均为凸函数,则二者的逐点最大函数f
f(x)=max(f1(x),f2(x))
其定义域为domf=domf1∩domf2,仍然时凸函数
证明:
∀θ∈[0,1],x,y∈domf,则
f(θx+(1−θ)y)=max(f1(θx+(1−θ)y),f2(θx+(1−θ)y))≤max(θf1(x)+(1−θ)f1(y),θf2(x)+(1−θ)f2(y))≤θmax(f1(x),f2(x))+(1−θ)max(f1(y),f2(y))=θf(x)+(1−θ)f(y)
同理,可得出
f(x)=max(f1(x),f2(x),⋯,fm(x))
仍然是凸函数
铸点最大的性质可以扩展至无限个凸函数的逐点上确界。如果对于任意y∈A,函数f(x,y)关于x都是凸的,则函数g
g(x)=y∈Asupf(x,y)
关于x也是凸函数,定义域为
domg={x ∣ (x,y)∈domf∀y∈A,y∈Asupf(x,y)<∞}
sup:最小上界
- ∀s∈S⇒s≤sup(S)
标量复合函数
假设函数f:Rn→R,h:R→R,令
f(x)=h(g(x))
满足以下条件的时,f是凸函数
- h是凸函数,g是凸函数,h~是非减的
- h是凸函数,g是凹函数,h~是非增的
- h~:extended value extension of h
证明:
f′′(x)=h′′(g(x))g′(x)2+h′(g(x))g′′(x)
在实数域上,若g是凸函数,则g′′>0,若h是凸函数且非减,则h′′≥0,h′≥0,可以得出f′′≥0,即函数f是凸函数
| h |
g |
f |
| 凸函数,非减 |
凸函数 |
凸函数 |
| 凸函数,非增 |
凹函数 |
凸函数 |
| 凹函数,非减 |
凹函数 |
凹函数 |
| 凹函数,非增 |
凸函数 |
凹函数 |
矢量复合函数
f(x)=h(g(x))=h(g1(x),g2(x),⋯,gk(x))
满足以下条件的时,f是凸函数
- h是凸函数,g是凸函数,h~对于每个参数都是非减的
- h是凸函数,g是凹函数,h~对于每个参数都是非增的
- h~:extended value extension of h
证明:
f′′(x)=g′(x)T∇2h(g(x))g′(x)+∇h(g(x))Tg′′(x)
Jensen不等式及其扩展
基本不等式,也称Jensen不等式,如果f是凸函数,对于任意0≤θ≤1
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
如果f是凸函数,对于任意z∈domf,有
f(Ez)f(θ1x1+⋯+θkxk)θ1+≤Ef(z)⇓≤θ1f(x1)+⋯+θkf(xk)⋯+θk=1
共轭函数
方向导数
设S是Rn中的一个集合,f是定义在S上的实函数,x∈∫S(表示集合S的内部),d是非零向量,f在x沿着方向d的方向导数Df(x;d)定义为
Df(x;d)=λ→0limλf(x+λd)−f(x)
- fz在x处沿着方向d的右侧导数
Df(x;d)=λ→0+limλf(x+λd)−f(x)
- fz在x处沿着方向d的左侧导数
Df(x;d)=λ→0−limλf(x+λd)−f(x)
−D+f(x;−d)=D−f(x;d)
如果对某个x和方向d有
D+f(x;d)=D−f(x;d)
则存在方向导数
- 若方向d为单位向量ei,则f在x处沿方向导数正好等于f对xi的偏导数
- 如果f在x可微,则f在x处沿任何方向d的方向导数是有限的⇒Df(x,d)=dT∇f(x)
设f是一个凸函数,x∈Rn,在x处函数f(x)取有极值,则f在x处沿任何方向d的左侧导数及左侧导数都存在
梯度
定义函数:f:Rn→R
函数f的梯度为
∇f(x)=⎝⎜⎛∂x1∂f⋮∂xn∂f⎠⎟⎞∈Rn
- 是一个矢量
- 其方向上的方向导数最大,其大小正好是此最大方向导数
- 所有方向导数中会存在并且只存在一个最大值
- 偏导数连续才有梯度存在
通俗的来说,二维平面函数每个点只有一个切线,三位平面上一个点有无数个切线,而梯度就是这个点导数最大的切线的矢量。
Hessian矩阵
函数f所有二阶偏导数都存在并在定义域内连续,那么函数f的Hessian矩阵为
∇2f(x)=[成分(i,j)=∂xixj∂2f的矩阵]
- Hessian矩阵是对称矩阵
- Hessian矩阵的特征值形容其在该点附近特征向量方向的凹凸性,特征值越大,凸性越强。
假设在开集S⊂Rn上f∈C2(S),则f在x∈S的一阶泰勒展开式为
f(x)=f(x)+∇f(x)T(x−x)+o(∥x−x∥)
其中o(∥x−x∥)是当∥x−x∥→0时,关于∥x−x∥的高阶无穷小量
二阶泰勒展开式为
f(x)=f(x)+∇f(x)T(x−x)+21(x−x)T∇2f(x)(x−x)+o(∥x−x∥2)
其中o(∥x−x∥2)是当∥x−x∥2→0时,关于∥x−x∥2的高阶无穷小量
Hessian矩阵相关公式
设c,Q∈Rn
- ∇(cTx)=c
- ∇(xQTx)=Q+QTx=2Qx
- ∇2(xTQx)=Q+QT=2Q
- ∇f(x)=Qx+c, ∇2f(x)=Q
二次函数的Hessian矩阵
二次函数可以写成以下形式
f(x)=21xAx+bTx+c
- 其中A是对称矩阵,b是n维向量
- 梯度:∇f(x=Ax+b
- Hessian矩阵:∇2f(x)=A
无约束优化问题
设函数f:Rn→R是二次可微函数(意味着domf是开集),求解
minf(x)
由于函数可微,则最优点x∗应该满足
f(x∗)=0,(x∗:local min)
- 可以通过解析求解最优性方程
- 采用迭代算法求解方程f(x∗)=0
- 即计算点列x0,x1,⋯,xk∈domf
- 使k→∞时,f(xk)→infxf(x)
- 当f(xk)−infxf(x)≤ε时,算法终止,ε容许误差值
停留点

2变量的情况:
| 条件 |
结果 |
| {fxxfyy−fxy2>0fxx>0 |
极大点 |
| {fxxfyy−fxy2>0fxx<0 |
极小点 |
| fyy−fxy2<0 |
鞍点 |
| fyy−fxy2=0 |
不确定 |
多变量的情况:
| 条件 |
结果 |
| ∇f(x)=0,∇2f(x) 正定矩阵 |
局部极小点 |
| ∇f(x)=0,∇2f(x) 负定矩阵 |
局部极大点 |
| ∇f(x)=0,∇2f(x) 不定矩阵 |
鞍点 |
| det∇2f(x)=0 |
不确定 |
泰勒定理
设f:Rn→R,设Δd∈Rn,存在t∈(0,1),有
| 阶数 |
公式 |
对应方法 |
| C1函数 |
f(x+Δd)=f(x)+∇f(x+tΔd)TΔd |
最速下降法 |
| C2函数 |
f(x+Δd)=f(x)+∇f(x+tΔd)TΔd+21ΔdT∇2f(x+tΔd)Δd |
牛顿法,拟牛顿法 |
一阶近似的最优解
其意义是:函数从f(x)→f(x+Δd)的变化等于f在某一点的梯度和向量Δd的点积,这个点总能在x和x+Δd之间找到,但是每个Δd对应着不同的t,如果允许一定误差的话,可以用∇f(x)代替∇f(x+tΔd)进行估测,即
f(x+Δd)=f(x)+∇f(x)TΔd
因为
[f(x)+∇f(x)TΔd]−[f(x)+∇f(x+tΔd)TΔd]=(∇f(x)−∇f(x+tΔd))TΔd
如果Δd足够小,那么∇f(x)−∇f(x+tΔd)也足够小,从而误差也同样小

在几何上的表现为,假设f是一个一维函数,上诉做法即在点(x,f(x))做一条切线(一阶泰勒展开),在Δd足够小的情况下,这条切线和实际函数非常接近
泰勒定理为我们提供了一种搜索一个函数极小点的方法,我们可以选择一个初始点x0,如果选择一个方向Δd∈R且满足∇f(x)TΔd<0,则存在t>0,使得
f(x+tΔd)<f(x)
如此迭代下去,f(x)的取值会越来越小,最后收敛到一个局部最小点,这样的方法称作直线搜索,其主要问题就是找到
二阶近似的最优解
同理一阶近似的最优解,

1次:f(x+d)=f(x∗)+∇f(x)Td+残差
2次:f(x+d)=f(x∗)+∇f(x)Td+21dT∇2f(x)d+残差
1元:f(x+d)=f(x)+f′(x)d+21f′′(x)Td2+残差
下降方法
goal∇f(x∗)=0,(x∗:local min)
本算法将产生一个优化点列xk,k=1,2,⋯,其中
xk+1=xk+tkΔdk
并且tk>0(除非xk已经是最优点)
- 搜索步径:Δdk
- 比例因子:tk第k次迭代的步进
只要xk不是最优点,则有
f(xk+1)<f(xk)
对于xk∈domf,由凸性可知
∇f(xk)T(y−xk)y−xkyf(y)≥0≥0≥xk≥f(xk)
因此下降方法中搜索方向必须满足
∇f(xk)TΔdk<0
即
t→+0limtkf(xk+tkΔdk)−f(xk)<0
也就是负梯度方向的夹角必须是锐角(毕竟锐角才是向下的),这样的方向叫做下降方向
下降方法算法
求解初期点x∈domf,k:=0
重复进行:
- 停止条件:∥∇f(xk)∥<ε
- 决定下降方向:Δd
- 直线探索,选择步长:t>0
- 计算下一个点:xk+1=xk+tkΔdk
- k:=k+1
精确直线搜索
有时候我们会用一种叫做精确直线搜索的方法,其中t是通过沿着射线{x+tΔd∣t≥0}优化f而确定的
t=args≥0minf(x+sΔd)
考虑正定对称矩阵A∈Rn×n,b∈Rn,求解二次型函数
minf(x)=21xTAx+bTx
根据下降方法的定义,函数将变为f(xk+sΔdk),将这个形式写作ϕ(a)
ϕ(a)=f(xk+aΔdk)=21(xk+aΔdk)TA(xk+aΔdk)+bT(xk+aΔdk)=21(ΔdkTAΔdk)a2+(ΔdkT∇f(xk))a+f(xk)
这是一个关于a的二次函数,其中∇f(x)=Ax+b,由于A是正定矩阵,可以知道ΔdkTAΔdk>0,为了求得ϕ(a)的最小值,求得使dadϕ(a)=0的a即可
dadϕ(a)=(ΔdkTAΔdk)a+ΔdkT∇f(xk)=0
解得
ak=−ΔdkTAΔdkΔdkT∇f(xk)
这里ΔdkT∇f(xk)<0,所以ak>0
回溯直线搜索(Armijo条件)
实践中主要采用非精确直线搜索方法,因为实际中精确直线搜索一般无法使用,沿着射线{x+tΔd ∣ t≥0}优化f确定步长,只要f有足够的减少即可
回溯直线搜索算法
确定参数a∈(0,0.5),β∈(0,1),t=1,k:=0
重复进行:
- 如果f(x+tΔd)>f(x)+at∇f(x)TΔd,则t:=βt,k:=k+1
- 否则返回t
回溯直线搜索收束性
由于Δd是降下方向,∇f(x)TΔd<0,所以只要满足t足够小,就一定有
f(x+tΔd)≈f(x)+t∇f(x)TΔd<f(x)+at∇f(x)TΔd
因此回溯直线搜索方法最终会停止
- 常数a表示可以接受的f的减少量占基于线性外推预测的减少量比值
- a需要小于0.5
- 正常一般在0.01∼0.3之间,表示我们可以接受的f的减少量在基于线性外推预测的减少量的1%和30%之间
- β正常取值:
- 接近0.1:非常粗糙的搜索
- 接近0.8:不太粗糙的搜索
Wolfe条件
Wolfe条件是在Armijo条件基础之上的条件。
Wolfe条件算法
确定参数0<a1<a2<0.5,β∈(0,1),t=1,k:=0
重复进行:
- 如果
f(x+tΔd)a2∇f(x)TΔd>f(x)+a1t∇f(x)TΔd>∇f(x+tΔd)TΔd
则t:=βt,k:=k+1,否则返回t
直线搜索方法的收敛性
为了获得全局最优解,我们需要得到
其中最速下降方向−∇f(xk)与搜索步径Δd的夹角为
cosθk=∥−∇f(xk)∥⋅∥Δd∥−∇f(xk)TΔd
利普希茨连续条件(Zoutendijk条件)
假定函数f是在Rn下有界,且在初始点x0的开集合N={x ∣ f(x)≤f(x0)上连续可导,那么∀x,y∈N,∃L,使得
∥∇f(x)−∇f(y)∥≤L∥x−y∥
其中L称为利普希茨定数,不等式称为利普希茨连续,当下降法,比例因子满足Wolfe条件的时候,其点阵xk,k=1,2,⋯,满足以下不等式
k=0∑∞(∥dk∥∇f(xk)Tdk)2<∞
化简后得到Zoutendijk条件
k=0∑∞(∥∇f(xk)∥⋅cosθk)2<∞
由无限级数的收束条件可得
k→∞lim∥dk∥∇f(xk)Tdk=0⇕k→∞lim∥∇f(xk)T∥⋅cosθk=0
如果对于∀k,存在δ>0使得cosθk≥δ,则
k→∞lim∥∇f(xk)T∥=0
上式展现了生成点阵的全局的收束性,也就是说,满足∀k,存在δ>0使得cosθk≥δ的点阵xk,k=1,2,⋯如果存在,则
k→∞liminf∥∇f(xk)T∥=0
梯度下降方法
goal∇f(x∗)=0,(x∗:local min)
本算法用负梯度作搜索方向,即
Δdk=−∇f(xk)
梯度下降方法算法
求解初期点x∈domf,k:=0
重复进行:
- 停止条件:∥∇f(xk)∥<ε
- 决定下降方向:Δdk=−∇f(xk)
- 通过精确或回溯直线探索,选择步长t>0
- 计算下一个点:xk+1=xk+tkΔdk
- k:=k+1
梯度下降方法收敛性
// TODO
最速下降方法
对f(x+v)在x处进行一阶泰拉展开
f(x+v)≈f^(x+v)=f(x)+∇f(x)Tv
- ∇f(x)Tv:是f在x处沿方向v的方向导数
- 近似给出了f沿小的步径v会发生的变化
- 如果方向导数是负数,则步径v是下降方向
如选择v使其方向导数尽可能小
- 由于方向导数∇f(x)Tv是v的线性函数
- v→+∞,则方向导数充分小
- 为了使问题有意义,还必须限制v的大小
我们定义一个规范化的最速下降方向
Δdnsd=argmin{∇f(x)Tv ∣ ∥v∥=0}
一个最速下降方向使因为上述优化问题可能有多个最优解- 一个规范化的最速下降方向Δdnsd是一个能使f的线性近似下降最多的具有单位范数的步径
我们也可以把规范化的最速下降方向Δdnsd定义为
Δdnsd=argmin{∇f(x)Tv ∣ ∥v∥≤0}
- 单位球体中在−∇f(x)的方向上投影最长的方向
还可以将规范化的最速下降方向乘以一个特殊的比例因子,从而考虑下述非规范的最速下降方向Δdsd
Δdsd=∥∇f(x)∥∗∇f(x)TΔdnsd=−∥∇f(x)∥∗2
最速下降方法算法
求解初期点x∈domf,k:=0
重复进行:
- 停止条件:∥∇f(xk)∥<ε
- 决定下降方向:Δdsd或者Δdnsd
- 通过精确或回溯直线探索,选择步长t>0
- 计算下一个点:xk+1=xk+tkΔdsd/nsd
- k:=k+1
如果采用精确直线搜索方向,下降方向的比例因子不起作用,因此规范化或非规范化的方向都能用
- 采用
Euclid范数:
- Δdsd=−∇f(x)
- 采用
二次范数:
- Δdnsd=−(∇f(x)TP−1∇f(x))−1/2P−1∇f(x)
- Δdsd=−P−1∇f(x)
最速下降方法收敛性
// TODO
牛顿法
牛顿法采用的是二阶近似,见二阶近似的最优解
牛顿步径
对于x∈domf,称向量
Δdnt=−∇2f(x)−1∇f(x)
为f在x处的牛顿步径
- 除非∇f(x)=0,从∇2f(x)的正当性可知∇f(x)TΔdnt为下降方向
∇f(x)TΔdnt=−∇f(x)T∇2f(x)−1∇f(x)<0
牛顿法算法
求解初期点x∈domf,k:=0
重复进行:
- 停止条件:∥∇f(xk)∥<ε
- 决定牛顿方向:Δdnt
- 计算下一个点:xk+1=xk+Δdnt
- k:=k+1
牛顿减量
对于原始牛顿法,由于没有比例因子,对于非二次型目标函数,有时会使函数值上升,表明原始牛顿法不能保证函数值稳定的下降,于是我们定义
λ(z)=⎩⎪⎨⎪⎧(∇f(x)T∇2f(x)−1∇f(x))1/2or(ΔdntT∇2f(x)Δdnt)1/2
为x处的牛顿减量,我们可以将牛顿减量与二阶近似联系到一起
f(x)−yinff^(x)=f(x)−f^(x+Δdnt)=21λ(x)2
另外牛顿减量也出现在回溯直线搜索中,即
∇f(x)TΔdnt=−λ(x)2
这是在回溯直线搜索中使用的常数,也可以解释为f在x处沿牛顿步径方向的方向导数
−λ(x)2=∇f(x)TΔdnt=dtdf(x+Δdntt)∣∣∣t=0
阻尼牛顿法
在原始牛顿法的基础上,引入比例因子λ,也就是牛顿减量
λk=λ∈Rargminf(xk+λΔdnt)
阻尼牛顿法算法
求解初期点x∈domf,k:=0
重复进行:
- 计算牛顿步径和减量
- λ2=∇f(x)T∇2f(x)−1∇f(x)
- Δdnt=−∇2f(x)−1∇f(x)
- 如果λ2/2≤ϵ,则停止
- 通过回溯直线探索,选择步长t>0
- 计算下一个点:xk+1=xk+tΔdnt
- k:=k+1
拟牛顿法
在牛顿法的迭代中,需要计算Hessian矩阵
- 此计算时间复杂度较大
- 有时候Hessian矩阵不是正定矩阵
于是我们可以使用一个n阶矩阵Gk=G(xk)来近似代替∇2f(x)−1,且必须和∇2f(x)由相同的性质即正定对称矩阵
由
f(x+Δd)=f(x)+∇f(x+tΔd)TΔd+21ΔdT∇2f(x+tΔd)Δd
得到
f(x)≈f(xk+1)+∇f(xk+1)T(x−xk+1)+21(x−xk+1)T∇2f(xk+1)(x−xk+1)
此时,对两边取梯度
∇f(x)≈∇f(xk+1)+∇2f(xk+1)(x−xk+1)
取x=xk,化简可得
∇f(xk+1)−∇f(xk)≈∇2f(xk+1)(xk+1−xk)
上述就是拟牛顿法,当我们对∇2f(xk+1)做近似Bk+1,即可得到
∇f(xk+1)−∇f(xk)≈Bk+1(xk+1−xk)
拟牛顿法(DFP)
该算法通过对迭代的方法,对∇2f(xk+1)−1做近似,其格式为
Dk+1=Dk+ΔDk,k=0,1,2,⋯
其中D0一般取单位矩阵I,我们将ΔDk待定为
ΔDk=auuT+βvvT
其中a,β为待定系数,u,v为待定向量,这种形式保证了矩阵的对称性,我们将其带入式子中
xk+1−xk=(Dk+ΔDk)(∇f(xk+1)−∇f(xk))=(Dk−auuT+βvvT)(∇f(xk+1)−∇f(xk))
其中注意到以下式子,我们进行以下的赋值
{auT(∇f(xk+1)−∇f(xk))=1βvT(∇f(xk+1)−∇f(xk))=−1
得到
{a=uT(∇f(xk+1)−∇f(xk))1β=vT(∇f(xk+1)−∇f(xk))−1
我们再将上面的式子代回去,可以得到
u−v=(xk+1−xk)−Dk(∇f(xk+1)−∇f(xk))
为了使上式成立,我们可以取
{u=(xk+1−xk)v=Dk(∇f(xk+1)−∇f(xk))
再将此带入到a,β进行求值
aβ=(xk+1−xk)T(∇f(xk+1)−∇f(xk))1=(∇f(xk+1)−∇f(xk))T⋅Dk⋅(∇f(xk+1)−∇f(xk))−1
令s=xk+1−xk,y=∇f(xk+1)−∇f(xk),得到
∇Dk+1=skTykskskT−ykTDkykDkyk(Dkyk)T
DFP算法
求解初期点x∈domf,k:=0,D0=I
重复进行:
- 停止条件:∥∇f(xk)∥<ε
- 决定下降方向:Δdnt=−Dk∇f(xk)
- 计算比例因子
- 利用直线搜索得到步长:λk
- 令sk=λkΔdnt
- 计算下一个点:xk+1=xk+sk
- 令yk=∇f(xk+1)−∇f(xk)
- 计算Dk+1=Dk+skTykskskT−ykTDkykDkykykTDk
- k:=k+1
拟牛顿法(BFGS)
BFGS算法与DFP算法完全类似,只是把s,y的位置进行了对调
Bk+1=Bk+ΔBk,k=0,1,2,⋯
其中B0一般取单位矩阵I,我们将ΔBk待定为
ΔBk=auuT+βvvT
其中a,β为待定系数,u,v为待定向量,这种形式保证了矩阵的对称性,我们将其带入式子中
∇f(xk+1)−∇f(xk)=(Bk+ΔBk)(xk+1−xk)=(Bk−auuT+βvvT)(xk+1−xk)
我们进行以下的赋值
{auT(∇f(xk+1)−∇f(xk))=1βvT(∇f(xk+1)−∇f(xk))=−1
得到
{a=uT(∇f(xk+1)−∇f(xk))1β=vT(∇f(xk+1)−∇f(xk))−1
我们再将上面的式子代回去,可以得到
u−v=(∇f(xk+1)−∇f(xk))−Bk(xk+1−xk)
为了使上式成立,我们可以取
{u=∇f(xk+1)−∇f(xk)v=Bk(xk+1−xk)
再将此带入到a,β进行求值
aβ=(∇f(xk+1)−∇f(xk))T(xk+1−xk)1=(xk+1−xk)T⋅Bk⋅(xk+1−xk)−1
令s=xk+1−xk,y=∇f(xk+1)−∇f(xk),得到
∇Bk=ykTskykykT−skTBkskBksk(Bksk)T
BFGS算法
求解初期点x∈domf,k:=0,B0=I
重复进行:
- 停止条件:∥∇f(xk)∥<ε
- 决定下降方向:Δdnt=−(Bk)−1∇f(xk)
- 计算比例因子
- 利用直线搜索得到步长:λk
- 令sk=λkΔdnt
- 计算下一个点:xk+1=xk+sk
- 令yk=∇f(xk+1)−∇f(xk)
- 计算Bk+1=Bk+ykTskykykT−skTBkskBksk(Bksk)T
- k:=k+1
Sherman-Morrison公式
这是线性代数中,这是求解逆矩阵的一种方法
设A∈Rn×n为可逆矩阵,u,v为列向量,则当
{vTA−1u=−1uTv=−1
则
(A+uvT)−1=A−1−1+vTA−1uA−1vvTA−1
证明:
令X=A+uvT,Y=A−1−1+vTA−1uA−1uvTA−1
XY=(A+uvT)(A−1−1+vTA−1uA−1uvTA−1)=AA−1+uvTA−1−1+vTA−1uAA−1uvTA−1+uvTA−1uvTA−1=I+uvTA−1−1+vTA−1uuvTA−1+uvTA−1uvTA−1=I+uvTA−1−1+vTA−1uu(1+vTA−1u)vTA−1=I+uvTA−1−uvTA−1=I
Sherman-Morrison公式应用
令A=I,则有I+uvT可逆当且仅当vTu=−1
(I+uvT)−1=I−1+vTuuvT
若v=u,则1+uTu>0,所以I+uuT可逆
(I+uuT)−1=I−1+uTuuuT
拟牛顿法(H-BFGS)
还可以通过近似Hessian逆矩阵,进一步优化BFGS方法
Bk+1Bk+1−1=Bk+ΔBk=Bk+ykTskykykT−skTBkskBksk(Bksk)T=((Bk+ykTskykykT)−skTBkskBksk(Bksk)T)−1=(Bk+ykTskykykT)−1−1+skTBksk−(Bksk)T(Bk+ykTskykykT)−1(Bksk)(Bk+ykTskykykT)−1(−skTBkskBksk(Bksk)T)(Bk+ykTskykykT)−1=(Bk+ykTskykykT)−1+(Bk+ykTskykykT)−1skTBksk−(Bksk)T(Bk+ykTskykykT)−1(Bksk)Bksk(Bksk)T(Bk+ykTskykykT)−1
令(Bk+ykTskykykT)=H,化简得到
Bk+1−1=H−1+H−1skTBksk−(Bksk)T(H−1)(Bksk)Bksk(Bksk)TH−1
我们再来看看H=(Bk+ykTskykykT)
H−1=(Bk+ykTskykykT)−1=Bk−1−1+yTs1yTB−1yB−1yTsyyTB−1=Bk−1−yTs+yTB−1yB−1yyTB−1
我们现在关注H−1skTBksk−(Bksk)T(H−1)(Bksk)Bksk(Bksk)TH−1
=======H−1skTBksk−(Bksk)T(H−1)(Bksk)Bksk(Bksk)TH−1(Bk−1−yTs+yTB−1yB−1yyTB−1)skTBksk−(Bksk)T(Bk−1−yTs+yTB−1yB−1yyTB−1)(Bksk)Bksk(Bksk)T(Bk−1−yTs+yTB−1yB−1yyTB−1)(Bk−1−yTs+yTB−1yB−1yyTB−1)skTBksk−skTBksk+yTs+yTB−1ysTyyTsBksk(Bksk)T(Bk−1−yTs+yTB−1yB−1yyTB−1)sTyyTsyTs+yTB−1y(Bk−1−yTs+yTB−1yB−1yyTB−1)BssTB(Bk−1−yTs+yTB−1yB−1yyTB−1)sTyyTsyTs+yTB−1y(ssTB−yTs+yTB−1yB−1yyTB−1)(Bk−1−yTs+yTB−1yB−1yyTB−1)sTyyTsyTs+yTB−1y(ssT−yTs+yTB−1yssTyyTB−1−yTs+yTB−1yB−1yyTssT+(yTs+yTB−1y)2B−1yyTssTyyTB−1)sTyyTs(yTs+yTB−1y)ssT−sTyyTsssTyyTB−1−sTyyTsB−1yyTssT+(yTs+yTB−1y)sTyyTsB−1yyTssTyyTB−1sTyyTs(yTs+yTB−1y)ssT−sTysyTB−1−sTyB−1ysT+yTs+yTB−1yB−1yyTB−1
于是
Bk+1−1=H−1+H−1skTBksk−(Bksk)T(H−1)(Bksk)Bksk(Bksk)TH−1=H−1+sTyyTs(yTs+yTB−1y)ssT−sTysyTB−1−sTyB−1ysT+yTs+yTB−1yB−1yyTB−1=Bk−1−yTs+yTB−1yB−1yyTB−1+sTyyTs(yTs+yTB−1y)ssT−sTysyTB−1−sTyB−1ysT+yTs+yTB−1yB−1yyTB−1=Bk−1+sTyyTs(yTs+yTB−1y)ssT−sTysyTB−1−sTyB−1ysT=(I−sTysyT)B−1−B−1sTyysT+(sTy)2(yTs+yTB−1y)ssT=(I−sTysyT)B−1−(I−sTysyT)B−1sTyysT+sTyssT=(I−sTysyT)B−1(I−sTyysT)+sTyssT
通过使用2次公式,最终得到
Bk+1−1=(I−sTysyT)B−1(I−sTyysT)+sTyssT
H-BFGS算法
求解初期点x∈domf,k:=0,D0=I
重复进行:
- 停止条件:∥∇f(xk)∥<ε
- 决定下降方向:Δdnt=−Bk−1∇f(xk)
- 计算比例因子
- 利用直线搜索得到步长λk
- 令sk=λkΔdnt
- 计算下一个点:xk+1=xk+sk
- 令yk=∇f(xk+1)−∇f(xk)
- 计算Bk+1−1=(I−sTysyT)B−1(I−sTyysT)+sTyssT
- k:=k+1
约束优化问题
一阶约束优化问题的本质是在梯度的下降方向上,沿着约束的方向进行优化,最后达到与约束条件的梯度相同的一点,即局部最优点,然后利用凸函数的性质,即可得到全局最优点,
等式约束条件
拉格朗日乘数法
求定义域内约束在某个区域内函数的极值, 可使用Lagrange乘子法
mins.t.z=f(x,y)φ(x,y)=0
我们假定在(x0,y0)的某一领域内f(x,y)与φ(x,y)均有连续的一阶偏导数,而φy(x0,y0)=0,由隐函数存在定理可知,φ(x0,y0)=0确定一个连续且具有连续偏导数的函数y=ψ(x),将其带入后,得到
z=f(x,ψ(x))
于是原函数在(x0,y0)处所求的极值,变为函数z=f(x,ψ(x))在x=x0处取得的极值,由一元可导函数取得极值的必要条件可得
dxdz∣x=x0=fx(x0,y0)+fy(x0,y0)dxdy∣x=x0=0
由隐函数求导公式,得
dxdy∣x=x0=−φy(x0,y0)φx(x0,y0)
代入后得到
fx(x0,y0)−fy(x0,y0)φy(x0,y0)φx(x0,y0)=0
设φy(x0,y0)fy(x0,y0)=−λ,上述条件变为
⎩⎪⎨⎪⎧fx(x0,y0)+λφx(x0,y0)=0fy(x0,y0)+λφy(x0,y0)=0φ(x0,y0)=0
上述条件可以看作在点(局部最小点)(x0,y0)的f的梯度的方向与φ的梯度方向同线,且满足φ(x0,y0)=0
引进辅助函数(拉格朗日函数)
L(x,y)=f(x,y)+λφ(x,y)
可以看出
Lx(x,y)Ly(x,y)=fx(x0,y0)+λφx(x0,y0)=0=fy(x0,y0)+λφy(x0,y0)=0
将L(x,y)称为拉格朗日函数,参数λ称为拉格朗日乘子
拉格朗日乘数法算法
L(x,y)=f(x,y)+λφ(x,y)
- 分别求对x,y的一阶偏导数,使之为0,然后与所有方程进行联立
⎩⎪⎨⎪⎧fx(x,y)+λφx(x,y)=0fy(x,y)+λφy(x,y)=0φ(x,y)=0
由上述方程解出x,y,λ,这样得到的(x,y)就是函数f(x,y)在附加条件φ(x,y)=0下可能的极值点
拉格朗日乘数法算法推广
mins.t.u=f(x,y,z,t)φ(x,y,z,t)=0ϕ(x,y,z,t)=0
L(x,y,z,t)=f(x,y,z,t)+λφ(x,y,z,t)+μϕ(x,y,z,t)
其中λ,μ均为参数,求其一阶偏导数,并使之等于0,与原条件连理起来即可求解,即
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧fx(x,y,z,t)+λφx(x,y,z,t)+μϕx(x,y,z,t)=0fy(x,y,z,t)+λφy(x,y,z,t)+μϕy(x,y,z,t)=0fz(x,y,z,t)+λφz(x,y,z,t)+μϕz(x,y,z,t)=0ft(x,y,z,t)+λφt(x,y,z,t)+μϕt(x,y,z,t)=0φ(x,y,z,t)=0ϕ(x,y,z,t)=0
求解后得出的(x,y,z,t)就是函数f(x,y,z,t)在附加条件下的可能极值点,至于是否为真正的极值点,需要在实际问题中根据问题本身的性质来判定
拉格朗日乘数法算法总结
mins.t.f(x)hi(x)=0,i=1,2,⋯,n
拉格朗日函数
L(x,λ)=f(x)+i=1∑nλihi(x),i=1,2,⋯,n
对其求导
Lxi(x,λ)=fxi(x)+i=1∑nλihixi(x),i=1,2,⋯,n
联立原条件方程后即可得到解
Lxi(x,λ)=fxi(x)+i=1∑nλihixi(x)hi(x)=0i=1,2,⋯,n
不等式约束条件
不等式约束问题的一阶最优性条件
考虑下方非线性规划问题
mins.t.f(x)gi(x)>0,i=1,2,⋯,m
这个问题的可行域为
S={x∣gi(x)≥0,i=1,2,⋯,m}
对于x∈S,将约束条件gi(x)分为以下2中情况(其他I为下标集,即下标的集合)
I={i∣gi(x)=0}
- gi(x)=0,i∈I
满足等号的等式,在x的附近限制了可行点的范围,也就是在某些方向稍微移动一点,仍能满足约束条件,但是沿着另外一些方向,无论移动多少,也会违背约束条件,通俗的说就是在边界上。这样的约束条件称为在x处起作用的约束
- gi(x)>0,i∈/I
反之,对于大于号的不等式,在x的附近无论哪个方向,稍微离开一些距离都不会违背约束,通俗的说就是在不在边界上。这样的约束条件称为在x处不起作用的约束

可以用集合
G0={d∣∇gi(x)Td>0,i∈I}
取代可行域。
定理:设x∈S,f(x)和gi(x)(i∈I)在x可微,gi(x)(i∈/I)在x连续,如果x是非线性规划问题的局部最优解,则
下降方向集∩G0=∅
Fritz John条件
设
- x∈S
- I={i∣gi(x)=0}
- f,gi(i∈I)在x处可微
- gi(i∈/I)在x处连续
如果x是非线性规划问题的局部最优解,则存在不全为0的非负数w0,wi(i∈I),使得
w0∇f(x)−i∈I∑wi∇gi(x)=0
证明:根据上面下降方向集∩G0=∅,即不等式
{∇f(x)Td<0−∇gi(x)Td<0,i∈I
无解,再由超平面分离定理(两个凸集分离,直观地看是指两个凸集合没有交叉和重合的部分,因此可以用一张超平面将两者隔在两边),必存在非零向量
w=(w0,wi,i∈I)≥0
使得
w∇f(x)−i∈I∑wi∇gi(x)=0
在使用Fritz John条件时,可能出现w0=0的情况,这时候Fritz John条件中不包含目标函数的任何数据,只是把起作用的约束的梯度组合成了零向量。这样的解的描述没有价值,我们需要w0=0的情况,为了保证这样,我们需要添加某种限制,这样的限制称为约束规格,在定理Fritz John条件中,如果增加起作用约束的梯度线性无关的约束规格,则给出不等式约束问题的K-T条件
Kuhn-Tucker条件
考虑非线性规划问题,设
- x∈S
- I={i∣gi(x)=0}
- f,gi(i∈I)在x处可微
- gi(i∈/I)在x处连续
- {∇gi(x)∣i∈I}线性无关
如果x是非线性规划问题的局部最优解,则存在非负数wi,i∈I,使得
∇f(x)−i∈I∑mwi∇gi(x)=0
证明:
根据Fritz John条件,有
w0∇f(x)−i∈I∑mwi∇gi(x)=0
w0不能为0,如果为0,则会导致{∇gi(x)∣i∈I}线性相关,于是可以使
wi=w0wi^,i∈I
从而得到
{∇f(x)−∑i∈Imwi∇gi(x)=0wi≥0,i∈I
若gi(i∈/I)在x处可微,则K-T条件可写成等价形式:
⎩⎪⎨⎪⎧∇f(x)−∑i=1mwi∇gi(x)=0wigi(x)=0,i=1,⋯,mwi≥0,i=1,⋯,m
- 当i∈/I时,gi(x)=0,由上面的条件可以知道wi=0,这时,项wigi(x)自然消去,得到上面的等式。
- 当i∈I时,gi(x)=0,因此条件wigi(x)=0对wi没有限制
条件wigi(x)称为互补松弛条件
- ∇f(x)−∑i=1mwi∇gi(x)=0含有m+n个未知量及m+n个方程的方程组
- 如果给定点x,验证它是否为K-T点,只需要解方程组∇f(x)−∑i∈Iwi∇gi(x)=0
- 如果x没有给定,欲求问题的K-T点,就需要解上述的等价形式的方程
∇f(x)−∑i=1mwi∇gi(x)=0实质是在x时,f的梯度方向等于g的方向
对于凸优化,也有最优解的一阶充分条件
定理:在非线性规划问题中,设
- f是凸函数
- gi(i=1,⋯,m)是凹函数
- S为可行域,x∈S
- I={i∣gi(x)=0}
- f,gi(i∈I)在x处可微
- gi(i∈/I)在x处连续
- 在x处K-T条件成立
则x为全局最优解
一般约束问题的一阶最优性条件
记
g(x)=⎝⎜⎜⎜⎛g1(x)g2(x)⋮gm(x)⎠⎟⎟⎟⎞,h(x)=⎝⎜⎜⎜⎛h1(x)h2(x)⋮hl(x)⎠⎟⎟⎟⎞
将非线性规划问题写作
mins.t.s.t.f(x),x∈Rng(x)≥0h(x)=0
正则点
定义:设x为可行点,不等式约束中在x起作用约束下标集记作I,如果向量组
{∇gi(x),∇hj(x)∣i∈I,j=1,2,⋯,l}
线性无关,就称x为约束g(x)≥0和h(x)=0的正则点
切平面
点集{x=x(t)∣t0≤t≤t1}称为曲面S={x∣h(x)=0}上的一条曲线,如果对所有t∈[t0,t1]均有
h(x(t))=0
显然,曲线上的点是参数t的函数,如果导数x′(t)=dtdx(t)存在,则称曲线是可微的
- 曲线x(t)的一阶导数x′(t)是曲线在点x(t)处的切向量
- 曲面S上在点x处所有可微曲线的切向量组成的集合,称为曲面S在点x的切平面,记作T(x)
为了表达切平面,定义下列子空间
H={d∣∇h(x)Td=0}
其中∇h(x)=(∇h1(x),∇h2(x),⋯,∇h1(x)),∇hj(x)是hj(x)的梯度
根据切平面T及子空间H的定义,在点x,若向量d∈T(x),则有
d∈Hdef{d∣∇h(x)Td=0}
反之不一定成立,但若x是约束h(x)=0的正则点,反之也成立
定理:设x是曲面S={x∣h(x)=0}上一个正则点(即∇hi(x)线性无关),则在点x的切平面T(x)等于子空间H={d∣∇h(x)Td=0}
Fritz John条件丨最优解的一阶必要条件
定理:设在约束极值问题中
- x为可行点
- I={i∣gi(x)=0}
- f,gi(i∈I)在x处可微
- gi(i∈/I)在x处连续
- 且∇hi(x)∣i=1,2,⋯,l}线性无关
如果x是非线性规划问题的局部最优解,则在x处,有
下降方向集∩G0∩切平面=∅
如果x是局部最优解,则存在不全为0的w0,wi(i∈I)和vj(j=1,⋯,j),使得
w0∇f(x)−i∈I∑wi∇gi(x)−j=1∑lvj∇hj(x)=0,w0,wi≥0,i∈I
证明:
如果∇hi(x)线性相关,则存在不全为0的数,使得∑j=1lvj∇hj(x)=0,令w0,wi=0即可得出答案。
如果线性无关,由下降方向集∩G0∩切平面=∅,即不等式组
⎩⎪⎨⎪⎧∇f(x)Td<0−∇gi(x)Td<0,i∈I∇hj(x)Td=0,j=1,⋯,l
无解
- 令A是以∇f(x)T,−∇gi(x)T为行组成的矩阵
- 令B是以−hj(x)T为组成的矩阵
上述不等式组化为
{Ad<0Bd=0
非空凸集的分离定理:设S1和S2是Rn中两个非空凸集,S1∩S2=∅,则存在非零向量p,使得
inf{pTx∣x∈S1}≥sup{pTx∣x inS2}
定义两个集合
S1S2={[y1y2]∣y1=Ady2=Bd,d∈Rn}={[y1y2]∣y1<0y2=0}
它们都是非空凸集,并且
S1∩S2=∅
根据非空凸集的分离定理,存在非零向量
p=[p1p2]
使得对任意d∈Rn及每一个点[y1y2]∈clS2成立
p1TAd+p2TBd≥p1Ty1+p2Ty2
因为令y2=0,且y1的每个分量可为任意负数,因此p1≥0,在令
[y1y2]=[00]∈clS2
则又可得出
p1TAd+p2TBd≥0
因为d∈Rn,令d=−(ATp1+BTp2),带入后得到
−∥ATp1+BTp2∥2≥0
于是得到
ATp1+BTp2=0
- 将p1的分量记作w0和wi(i∈I)
- 将p2的分量记作vj(j=1,⋯,l)
则上式变为
w0∇f(x)−i∈I∑wi∇gi(x)−j=1∑lvj∇hj(x)=0,w0,wi≥0,i∈I
同理,为了保证w0不为零,需要非约束条件加上某种限制,即为K−T必要条件
Kuhn-Tucker条件丨最优解的一阶必要条件
设在非线性规划问题
- x为可行点
- I={i∣gi(x)=0}
- f,gi(i∈I)在x处可微
- gi(i∈/I)在x处连续
- 且∇gi,∇hi(x)∣i=1,2,⋯,l}线性无关
如果x是非线性规划问题的局部最优解,则存在wi,i∈I,使得
∇f(x)−i∈I∑wi∇gi(x)−j=1∑lvj∇hj(x)=0,wi≥0,i∈I
证明:
根据Fritz John条件,有不全为0的w0,wi(i∈I)和vj(j=1,⋯,l),使得
w0∇f(x)−i∈I∑wi∇gi(x)−j=1∑lvj∇hj(x)=0,w0,wi≥0,i∈I
由向量组∇gi,∇hi(x)∣i=1,2,⋯,l}线性无关,比得出w0=0,若不然会导致线性相关,令
wivj=w0wi,=w0vj,i∈Ij=1,⋯,l
带入化简后得到
∇f(x)−i∈I∑m∇gi(x)−j=1∑lvj∇hj(x)=0,wi≥0,i∈I
与不等式约束的情形类似,当gi(i∈/I)在点x也可微时,令其相应的乘子wi=0,于是可将上述K-T条件转化为下列等价形式
⎩⎪⎨⎪⎧∇f(x)−∑i∈Im∇gi(x)−∑j=1lvj∇hj(x)=0wigi(x)=0,i=1,2,⋯,mwi≥0,i=1,2,⋯,m
其中wigi(x)=0仍被称为互补松弛条件
∇f(x)−∑i∈Im∇gi(x)−∑j=1lvj∇hj(x)=0实质是在x时,f的梯度方向等于g的梯度方向等于h的梯度方向
广义拉格朗日
定义广义的拉格朗日函数
L(x,w,v)=f(x)−i=1∑mwigi(x)−j=1∑lvihj(x)
在K-T条件下,若x为非线性规划问题的局部最优解,则存在乘子向量w≥0和v,使得
∇xL(x,w,v)=0
这样,K-T乘子w和v也称为拉格朗日乘子,此时一般情形的一阶必要条件可以表达为
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∇xL(x,w,v)=0∇vL(x,w,v)=h(x)=0∇wL(x,w,v)=g(x)>0wigi(x)=0,i=1,⋯,mwi≥0,i=1,⋯,m
对于凸优化,也有最优解的一阶充分条件
定理:在非线性规划问题中,设
- f是凸函数
- gi(i=1,⋯,m)是凹函数
- hj(j)=1,⋯,l是线性函数
- S为可行域,x∈S
- I={i∣gi(x)=0}
- 在x处K-T条件成立
即存在wi≥0(i∈I)及vj(j=1,⋯,l),使得
∇f(x)−i∈I∑mwi∇gi(x)−j=1∑lvj∇hj(x)=0
则x为全局最优解
不是凸优化的话,K-T条件只是极小值点的必要条件,不是充分条件,K-T点是驻点,是可能的极值点。
K-T条件总结
| 问题 |
拉格朗日函数 |
K-T条件 |
| mins.t.f(x)g(x)=0 |
L(x,λ)=f(x)−λg(x) |
{∇xL(x,λ)=∇f(x)−λ∇g(x)=0∇λL(x,λ)=g(x)=0 |
| mins.t.f(x)g(x)≥0 |
L(x,λ)=f(x)−λg(x) |
⎩⎪⎪⎪⎨⎪⎪⎪⎧∇xL(x,λ)=∇f(x)−λ∇g(x)=0∇λL(x,λ)=g(x)≥0λg(x)=0λ≥0 |
| mins.t.f(x)g(x)≤0 |
L(x,λ)=f(x)+λg(x) |
⎩⎪⎪⎪⎨⎪⎪⎪⎧∇xL(x,λ)=∇f(x)+λ∇g(x)=0∇λL(x,λ)=g(x)≤0λg(x)=0λ≥0 |
| mins.t.f(x)g(x)≥0h(x)=0 |
L(x,λ,μ)=f(x)−λg(x)−μh(x) |
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∇xL(x,λ,μ)=∇f(x)−λ∇g(x)−μ∇h(x)=0∇λL(x,λ,μ)=g(x)≥0∇μL(x,λ,μ)=h(x)=0λg(x)=0λ≥0 |
| mins.t.f(x)g(x)≤0h(x)=0 |
L(x,λ,μ)=f(x)+λg(x)−μh(x) |
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∇xL(x,λ,μ)=∇f(x)+λ∇g(x)−μ∇h(x)=0∇λL(x,λ,μ)=g(x)≤0∇μL(x,λ,μ)=h(x)=0λg(x)=0λ≥0 |
参考文献