huhu's Blog

FLOWER ON THE PRECIPICE

[线性代数] - 四个子空间

发表于 更新于 分类于
本文字数： 3.8k 阅读时长 ≈ 3 分钟

定义

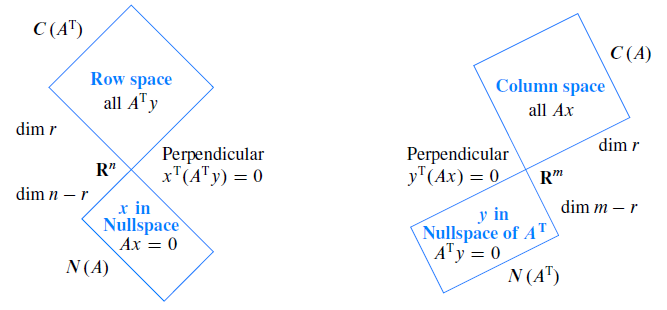
设A\mathbf{A}是m×nm \times n的矩阵，定义以下四个子空间

名称 符号 集合 维数
列空间 C(A)C(\mathbf{A}) {Ax ∣ ∀x∈Rn}\lbrace{}\mathbf{A}\mathbf{x}\ \mid \ \forall \mathbf{x} \in \mathbb{R}^n\rbrace{} rr
行空间 C(AT)C(\mathbf{A}^T) {ATy ∣ ∀y∈Rm}\lbrace{}\mathbf{A}^T\mathbf{y}\ \mid\ \forall \mathbf{y} \in \mathbb{R}^m\rbrace{} rr
零空间 N(A)N(\mathbf{A}) {x ∣ ∀x∈Rn,Ax=0}\lbrace{}\mathbf{x}\ \mid\ \forall \mathbf{x} \in \mathbb{R}^n, \mathbf{A}\mathbf{x} = 0\rbrace{} n−rn-r
左零空间 N(AT)N(\mathbf{A}^T) {y ∣ ∀y∈Rm,ATy=0}\lbrace{}\mathbf{y}\ \mid\ \forall \mathbf{y} \in \mathbb{R}^m, \mathbf{A}^T\mathbf{y} = 0\rbrace{} m−rm-r

性质1

C(A)⊥N(AT)C(AT)⊥N(A)\begin{aligned} C(\mathbf{A}) \perp N(\mathbf{A}^T) \\ C(\mathbf{A^T}) \perp N(\mathbf{A}) \end{aligned}

也就是在Rm\mathbb{R}^m中

C(A)=N(AT)⊥orC(A)⊥=N(AT)C(\mathbf{A}) = N(\mathbf{A}^T)^\perp \quad or \quad C(\mathbf{A})^\perp = N(\mathbf{A}^T)

在Rn\mathbb{R}^n中

C(AT)=N(A)⊥orC(AT)⊥=N(A)C(\mathbf{A}^T) = N(\mathbf{A})^\perp \quad or \quad C(\mathbf{A}^T)^\perp = N(\mathbf{A})

证明C(A)⊥=N(AT)C(\mathbf{A})^\perp = N(\mathbf{A}^T)

取∀x∈N(AT), ∀y∈C(A)\forall \mathbf{x} \in N(\mathbf{A}^T),\ \forall \mathbf{y} \in C(\mathbf{A})。则∃z∈Rn\exists \mathbf{z} \in \mathbb{R}^n，使得

y=Az\mathbf{y} = \mathbf{A}\mathbf{z}

计算xTy\mathbf{x}^T\mathbf{y}，其中注意到ATx=0\mathbf{A}^T\mathbf{x} = 0

xTy=xTAz=(ATx)Tz=0\mathbf{x}^T\mathbf{y} = \mathbf{x}^T\mathbf{A}\mathbf{z} = (\mathbf{A}^T\mathbf{x})^T\mathbf{z} = 0

即可得出

x⊥y→x∈C(A)⊥\mathbf{x} \perp \mathbf{y} \rightarrow \mathbf{x} \in C(\mathbf{A})^\perp

所以

N(AT)⊆C(A)⊥N(\mathbf{A}^T) \subseteq C(\mathbf{A})^\perp

取∀x∈C(A)⊥, ∀y∈C(A)\forall \mathbf{x} \in C(\mathbf{A})^\perp,\ \forall \mathbf{y} \in C(\mathbf{A})。则∃z∈Rn\exists \mathbf{z} \in \mathbb{R}^n，使得

y=Az\mathbf{y} = \mathbf{A}\mathbf{z}

则因为x,y\mathbf{x},\mathbf{y}的空间互为正交补

xTy=xTAz=(ATx)Tz=0\mathbf{x}^T\mathbf{y} = \mathbf{x}^T\mathbf{A}\mathbf{z} = (\mathbf{A}^T\mathbf{x})^T\mathbf{z} = 0

因为z∈Rn\mathbf{z} \in \mathbb{R}^n，所以

ATx=0\mathbf{A}^T\mathbf{x} = 0

即

x∈N(AT)\mathbf{x} \in N(\mathbf{A}^T)

即可得出

C(A)⊥⊆N(AT)C(\mathbf{A})^\perp \subseteq N(\mathbf{A}^T)

综上

{N(AT)⊆C(A)⊥C(A)⊥⊆N(AT)⇒N(AT)=C(A)⊥\begin{cases} N(\mathbf{A}^T) \subseteq C(\mathbf{A})^\perp \\ C(\mathbf{A})^\perp \subseteq N(\mathbf{A}^T) \end{cases} \Rightarrow N(\mathbf{A}^T) = C(\mathbf{A})^\perp

证明C(AT)⊥=N(A)C(\mathbf{A}^T)^\perp = N(\mathbf{A})

取∀x∈N(A), ∀y∈C(AT)\forall \mathbf{x} \in N(\mathbf{A}),\ \forall \mathbf{y} \in C(\mathbf{A}^T)。则∃z∈Rn\exists \mathbf{z} \in \mathbb{R}^n，使得

y=ATz\mathbf{y} = \mathbf{A}^T\mathbf{z}

计算xTy\mathbf{x}^T\mathbf{y}，其中注意到ATx=0\mathbf{A}^T\mathbf{x} = 0

xTy=xTATz=(Ax)Tz=0\mathbf{x}^T\mathbf{y} = \mathbf{x}^T\mathbf{A}^T\mathbf{z} = (\mathbf{A}\mathbf{x})^T\mathbf{z} = 0

即可得出

x⊥y→x∈C(AT)⊥\mathbf{x} \perp \mathbf{y} \rightarrow \mathbf{x} \in C(\mathbf{A}^T)^\perp

所以

N(A)⊆C(AT)⊥N(\mathbf{A}) \subseteq C(\mathbf{A}^T)^\perp

取∀x∈C(AT)⊥, ∀y∈C(AT)\forall \mathbf{x} \in C(\mathbf{A}^T)^\perp,\ \forall \mathbf{y} \in C(\mathbf{A}^T)。则∃z∈Rn\exists \mathbf{z} \in \mathbb{R}^n，使得

y=ATz\mathbf{y} = \mathbf{A}^T\mathbf{z}

则因为x,y\mathbf{x},\mathbf{y}的空间互为正交补

xTy=xTATz=(Ax)Tz=0\mathbf{x}^T\mathbf{y} = \mathbf{x}^T\mathbf{A}^T\mathbf{z} = (\mathbf{A}\mathbf{x})^T\mathbf{z} = 0

因为z∈Rn\mathbf{z} \in \mathbb{R}^n，所以

Ax=0\mathbf{A}\mathbf{x} = 0

即

x∈N(A)\mathbf{x} \in N(\mathbf{A})

即可得出

C(AT)⊥⊆N(A)C(\mathbf{A}^T)^\perp \subseteq N(\mathbf{A})

综上

{N(A)⊆C(AT)⊥C(AT)⊥⊆N(A)⇒C(AT)⊥=N(A)\begin{cases} N(\mathbf{A}) \subseteq C(\mathbf{A}^T)^\perp \\ C(\mathbf{A}^T)^\perp \subseteq N(\mathbf{A}) \end{cases} \Rightarrow C(\mathbf{A}^T)^\perp = N(\mathbf{A})