[概率论] - 概率论基本知识

基本概念

• 样本空间：随机试验$E$的所有可能结果组成的集合，记为$S$
• 样本点：$E$的每个结果
• 随机事件：试验$E$的样本空间$S$的子集，简称事件
• 事件发生：当且仅当这一子集中的一个样本点出现的情况
  • 必然事件：每次实验中总是发生的
  • 不可能事件：每次实验中都不发生。记作$\varnothing$

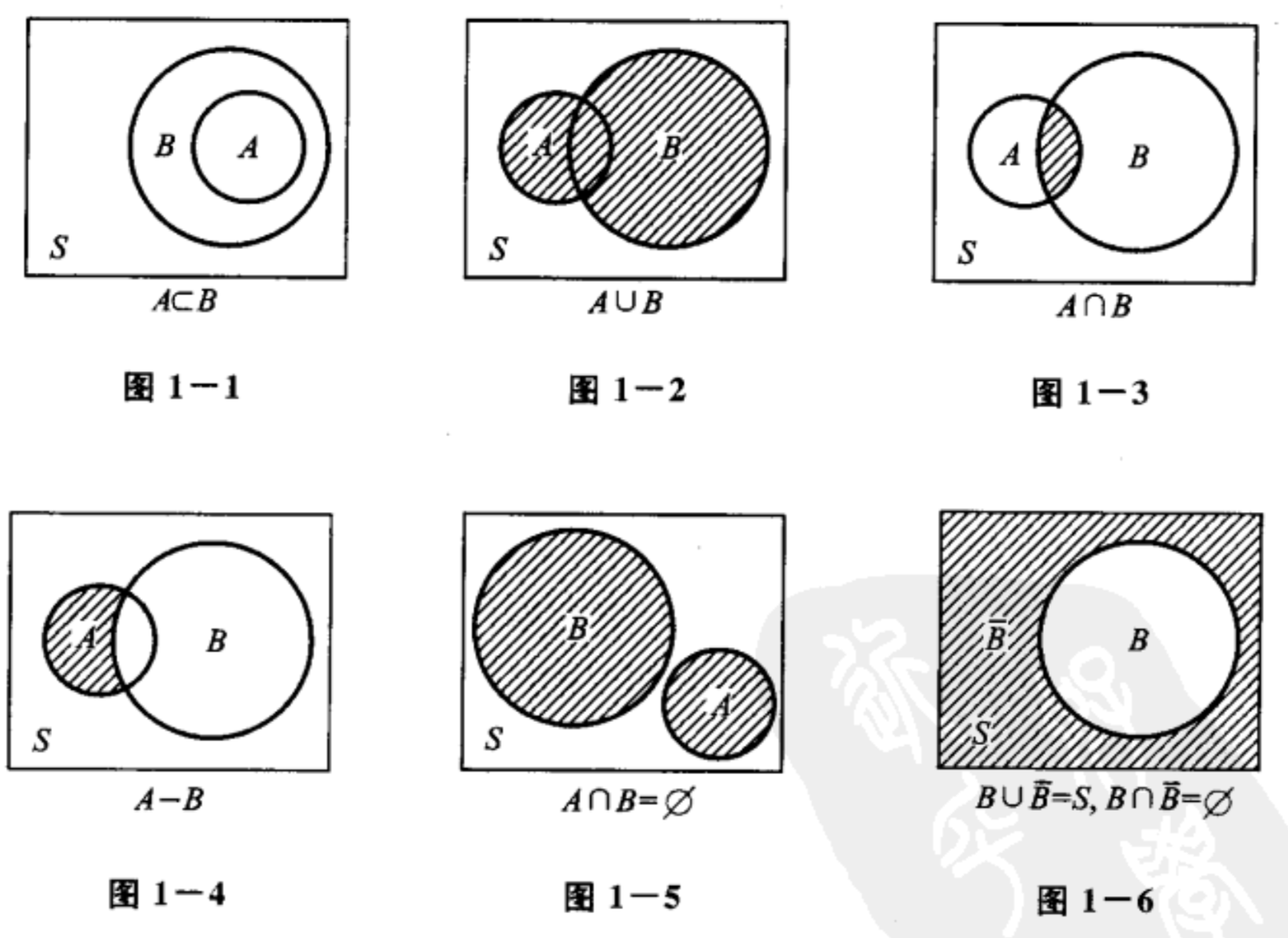
事件关系

• 包含：若$A \subset B$，则称事件$B$包含事件A，指事件A发生必导致事件B发生
• 相等：若$A \subset B$且$B \subset A$，既$A = B$，称事件$A$与事件$B$相等
• 和事件：事件$A \cup B = \lbrace x | x \in A\text{或}x \in B\rbrace$称为事件$A$与事件$B$的和事件
• 积事件：事件$A \cap B = \lbrace x | x \in A\text{且}x \in B\rbrace$称为事件$A$与事件$B$的积事件
• 差事件：事件$A - B = \lbrace x | x \in A\text{且}x \notin B\rbrace$称为事件$A$与事件$B$的差事件
• 互不相容：$A \cap B = \varnothing$，称为互不相容或互斥的
• 逆事件：$A \cup B = S$，称为逆事件或者对立事件，B相对于A记作$\overline{A}$

$\begin{aligned} \bigcup^n_{k=1}A_k \qquad \bigcap^n_{k=1}A_k \\ \text{和事件} \qquad\ \ \ \ \ \text{积事件} \end{aligned}$

频率

在相同的条件下，进行了n此实验

• 频数：事件$A$发生的次数$n_A$
• 频率：比值$n_A/n$，记作$f_n(A)$

频率的性质：

• $0 \leq f_n(A) \leq 1$
• $f_n(S) = 1$
• $f_n(\bigcup^n_{k=1}A_k) = \sum^n_{k=1}f(A_k)$

概率

概率：设$E$是随机实验，$S$是他的样本空间，对于$E$的每一事件$A$赋予一个实数，记为$P(A)$

• 非负性：对于每一个事件有$P(A) \geq 0$
• 规范性：对于必然事件$S$，有$P(S) = 1$
• 可列可加性：设$A_i,A_j$是两两互不相容事件，则$A_iA_j = \varnothing, i \neq j$

$P(A_i \cup A_j) = P(A_i) + P(A_j)$

如果不是互不相容，则

$P(A_i \cup A_j) = P(A_i) + P(A_j) - P(A_iA_j)$

实际推断原理：概率很小的事件在一次试验中实际上几乎是不发生的

等可能概率

• 试验的样本空间只包含有限个元素
• 试验中每个基本事件发生的可能性相同

这种试验称为等可能概率，也称为古典概率，
设试验的样本空间为$S = \lbrace e_1, e_2, \cdots, e_n \rbrace$

$P(\lbrace e_1 \rbrace) = P(\lbrace e_2 \rbrace) = \cdots = P(\lbrace e_1 \rbrace)$

条件概率

事件$A$发生的条件下事件$B$发生的条件概率

$P(B|A) = \frac{P(AB)}{P(A)}$

• $P(B|A)$：事件$A$已经发生的条件下事件$B$发生的概率
• $P(AB)$：事件$A$与事件$B$同时发生的概率

性质:

• 非负性：对于每一个事件有$P(B|A) \geq 0$
• 规范性：对于必然事件$S$，有$P(S|A) = 1$
• 可列可加性：设$B_1,B_2,\cdots$是两两互不相容事件，则

$P(\bigcup^\infty_{i=1} B_i| A) = \sum^\infty_{i=1}P(B_i|A)$

乘法定理

设$P(A) > 0$，则有乘法公式：

$\begin{aligned} P(AB) &= P(B|A)P(A) \\ P(ABC) &= P(C|AB)P(B|A)P(A) \end{aligned}$

可推广到$n$个事件

$P(A_1A_2\cdots A_n) = P(A_n|A_1A_2\cdots A_{n-1})P(A_{n-1}|A_1A_2\cdots A_{n-2})\cdots P(A_2|A_1)P(A_1)$

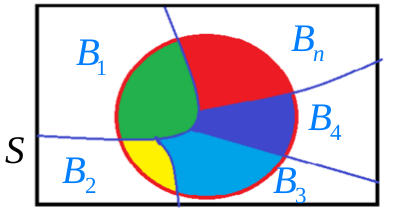
划分

设$S$为试验$E$的样本空间，$B_1,B_2,\cdots,B_n$为$E$的一组事件，若

• $B_iB_j = \varnothing, i \neq j, i, j =1,2,\cdots, n$
• $\bigcup^n_{k=1}B_k = S$

则称$B_1,B_2,\cdots,B_n$为样本空间$S$的一个划分

对于每次实验，划分中的事件必有且仅有一个发生

全概率公式

设试验$E$的样本空间为$S$，$A$为$E$的事件，$B_1,B_2,\cdots,B_n$为$S$的一个划分，且$P(B_i) > 0 (i=1,2,\cdots,n)$，则

$\begin{aligned} P(A) &= P(A|B_1)P(B_1)+P(A|B_2)P(B_2) + \cdots + P(A|B_n)P(B_n) \\ &= \sum^n_{i=1}P(A|B_i)P(B_i) \end{aligned}$

贝叶斯公式

设试验$E$的样本空间为$S$，$A$为$E$的事件，$B_1,B_2,\cdots,B_n$为$S$的一个划分，且$P(A) > 0, P(B_i) > 0 (i=1,2,\cdots,n)$，则

$P(B_i|A) = \frac{P(B_iA)}{P(A)} = \frac{P(A|B_i)P(B_i)}{\sum^n_{j=1}P(A|B_j)P(B_j)}, \quad i = 1,2,\cdots,n$

独立性

设$A,B$是两事件，如果满足等式

$P(AB) = P(A)P(B)$

则称事件$A,B$相互独立，简称$A,B$独立

• $A,B$相互独立与$A,B$互不相容不能同时成立
• 若$A,B$相互独立，则$P(B|A) = P(B)$
• 若$A,B$相互独立，则$A$与$\overline{B}$，$\overline{A}$与$B$，$\overline{A}$与$\overline{B}$也相互独立

独立事件可能重叠，不相容事件不重叠

随机变量

随机变量：设随机试验的样本空间为$S = \lbrace e \rbrace$，$X = X(e)$是定义在样本空间$S$上的实值单值函数，称$X = X(e)$为随机变量，简称为$X$

离散型随机变量

离散型随机变量：取到的值是有无限个或可列无限多个。
设离散型随机变量$X$所有可能的取值为$x_k(k=1,2,\cdots)$，$X$取各个可能值的概率，即事件$\lbrace X=x_k \rbrace$的概率为

$P(X = x_k) = p_k, \quad k =1,2,\cdots$

此式为离散型随机变量$X$的分布律

• $p_k \geq 0, \quad k=1,2,\cdots$
• $\sum^\infty_{n=1}p_k = 1$

离散型随机变量分布函数

设$X$是一个随机变量，$x$是任意实数，函数

$F(x) = P(X \leq x), \quad \infty < x < \infty$

称为$X$的分布函数
对于任意实数$x_1,x_2(x_1 < x_2)$，有

$\begin{aligned} P(x_1 < X \leq x_2) &= P(X \leq x_2) - P(X \leq x_1) \\ &= F(x_2) - F(x_2) \end{aligned}$

• 分布函数$F(x)$在$x$处的函数值就表示X落在区间$(-\infty, x]$上的概率
• $F(x)$是一个不减函数
• $0 \leq F(x) \leq 1$，$\lim_{x\rightarrow \pm \infty}F(x) = 0$

连续性随机变量

对于随机变量$X$的分布函数$F(x)$，存在非负函数$f(x)$，使对于任意实数$x$有

$F(x) = \int^x_{-\infty}f(t)dt$

则称$X$为连续型随机变量

连续性随机变量概率密度

函数$f(x)$称为$X$的概率密度函数，简称概率密度

• $f(x) \geq 0$
• $\int^\infty_{-\infty}f(x)dx = 1$
• $\forall x_1,x_2(x_1 \leq x_2) \rightarrow P(x_1 < X \leq x_2) = F(x_2) - F(x_1) = \int^{x_2}_{x_1}f(x)dx$
• 若$f(x)$在点$x$处连续，则有$F'(x) = f(x)$

多维随机变量

设$E$是一个随机试验，他的样本空间是$S = \lbrace e \rbrace$，设$X = X(e)$和$Y = Y(e)$是定义在$S$上的随机变量，他们组成一个向量$(X, Y)$叫做二维随机向量或二维随机变量

• 二元随机变量的性质依赖$X$和$Y$，和它们之间的相互关系

二维随机变量分布函数

设$(X,Y)$是二维随机变量，对于任意实数$x,y$，二元函数

$F(x,y) = P((X \leq x) \cup (Y \leq y)) =P(X \leq x, Y \leq y)$

称为二维随机变量$(X,Y)$的分布函数，或称为随机变量$X$和$Y$的联合分布函数

• $F(x,y)$是变量$x$和$y$的不减函数
• $0 \leq F(x,y) \leq 1$
• $F(x+0, y) = F(x,y), F(x, y+0)=F(x,y)$

二维离散型的随机变量

如果二维随机变量$(X,Y)$全部取到的值是有限对或可列无限多对，则为离散型的随机变量
设二维随机变量$(X,Y)$全部取到的值为$(x_i, y_j),i,j=1,2,\cdots$，即$P(X=x_i,Y=y_i)=p_{ij}$，则有

$p_{ij} \geq 0 \qquad\sum^\infty_{i=1}\sum^\infty_{j=1}p_{ij} = 1$

我们称$P(X=x_i, Y=y_i) = p_{ij},i,j=1,2,\cdots$为二维离散型随机变量$(X,Y)$的分布律，或随机变量$X$和$Y$的联合分布律

二维连续型的随机变量

对于二维随机变量$(X,Y)$的分布函数$F(x,y)$，如果存在非负的函数$f(x,y)$使对于任意$x,y$有

$F(x,y) = \int^y_{-\infty}\int^x_{-\infty}f(u,v)du,dv$

则称$(X,Y)$是连续型的二维随机变量，函数$f(x,y)$称为二维随机变量$(X,Y)$的概率密度或联合概率密度

• $f(x, y) \geq 0$
• $\int^\infty_{-\infty}\int^\infty_{-\infty}f(x,y)dxdy = F(\infty,\infty)= 1$
• 设$G$是$xOy$平面上的区域，点$(X,Y)$落在$G$内的概率为$P((X,Y) \in G) = \iint_G f(x,y)dxdy$
• 若$f(x)$在点$x$处连续，则有$\frac{\partial^2F(x,y)}{\partial x \partial y} = f(x,y)$

边缘分布

二元随机变量$(X,Y)$作为一个整体，具有分布函数$F(x,y)$
$X$和$Y$也各自有分布函数，记作$F_X(x), F_Y(y)$，依次称为二维随机变量$(X,Y)$关于$X$和$Y$的边缘分布函数

$\begin{aligned} F_X(x) &= P(X \leq x) = P(X \leq x, Y < \infty) = F(x, \infty) \\ F_Y(y) &= P(Y \leq y) = P(X < \infty, Y \leq y) = F(\infty, x) \end{aligned}$

离散型随机变量边缘分布

$F_X(x) = F(x, \infty) = \sum_{x_i \leq x}\sum^\infty_{j=1}p_{ij}$

可得

$\begin{aligned} P(X = x_i) &= \sum^\infty_{j=1}p_{ij}, \quad i=1,2,\cdots \\ P(Y = y_i) &= \sum^\infty_{i=1}p_{ij}, \quad j=1,2,\cdots \end{aligned}$

记

$\begin{aligned} p_{i \cdot} &= \sum^\infty_{j=1}p_{ij} = P(X = x_i), \quad i=1,2,\cdots \\ p_{\cdot j} &= \sum^\infty_{i=1}p_{ij} = P(Y = y_i), \quad j=1,2,\cdots \end{aligned}$

分别称$p_{i \cdot}$和$p_{\cdot j}$为$(X,Y)$关于$X$和关于$Y$的边缘分布律

连续型随机变量边缘分布

$F_X(x) = F(x, \infty) = \int^x_{-\infty}\left [\int^\infty_\infty f(x,y)dy\right ]dx$

可得

$\begin{aligned} f_X(x) &= \int^\infty_{-\infty}f(x,y)dy \\ f_Y(y) &= \int^\infty_{-\infty}f(x,y)dx \end{aligned}$

分别称$f_X(x)$和$f_Y(y)$为$(X,Y)$关于$X$和关于$Y$的边缘概率密度

条件分布

二维离散型随机变量条件分布

设$(X,Y)$是二维离散型随机变量，其分布律为

$P(X=x_i,Y=y_i) = p_{ij}, \quad i,j =1,2,\cdots$

$(X,Y)$关于$X$和关于$Y$的边缘分布律分别为

$\begin{aligned} P(X = x_i) &= P_{i\cdot} = \sum^\infty_{j=1}p_{ij}, \quad i=1,2,\cdots \\ P(Y = y_i) &= P_{\cdot j} = \sum^\infty_{j=1}p_{ij}, \quad j=1,2,\cdots \end{aligned}$

现在考虑在事件$Y=y_i$已发生的条件下$X=x_i$发生的概率，也就是求

$P(X=x_i|Y=y_i) = \frac{P(X=x_i,Y=y_i)}{P(Y=y_i)} = \frac{p_{ij}}{p_{\cdot j}}, \quad i = 1,2,\cdots$

• $P(X=x_i|Y=y_i) \leq 0$
• $\sum^\infty_{i=1}P(X=x_i|Y=y_i) = \sum^\infty_{i=1}\frac{p_{ij}}{p_{\cdot j}} = \frac{1}{p_{\cdot j}}\sum^\infty_{i=1}p_{ij} = \frac{p_{ij}}{p_{\cdot j}}, \quad i=1,2,\cdots$

在$Y = y_j$条件下随机变量$X$的条件分布律

$P(X = x_i|Y = y_i) = \frac{P(X = x_i, Y = y_i)}{P(Y = y_j)} = \frac{p_{ij}}{p_{\cdot j}}, \quad i=1,2,\cdots$

在$X = x_i$条件下随机变量$Y$的条件分布律

$P(Y = y_i|X = x_i) = \frac{P(X = x_i, Y = y_i)}{P(X = x_i)} = \frac{p_{ij}}{p_{i\cdot}}, \quad j=1,2,\cdots$

二维连续型随机变量条件分布

设二元随机变量$(X,Y)$的概率密度为$f(x,y)$，$(X,Y)$关于$Y$的边缘概率密度为$f_Y(y)$，若对于固定的$y$，$f_Y(y) > 0$，则称$\frac{f(x,y)}{f_Y(y)}$为在$Y=y$的条件下$X$的条件概率密度，记为

$f_{X|Y}(x|y) = \frac{f(x,y)}{f_Y(y)}$

称

$\int^x_{-\infty} f_{X|Y}(x|y)dx = \int^x_{-\infty}\frac{f(x,y)}{f_Y(y)}dx$

为在$Y=y$的条件下$X$的条件分布函数，记为$P(X \leq x | Y = y)$或$F_{X|Y}(x|y)$

同理，称

$\int^y_{-\infty} f_{Y|X}(y|x)dy = \int^y_{-\infty}\frac{f(y,x)}{f_X(x)}dy$

为在$X=x$的条件下$Y$的条件分布函数，记为$P(Y \leq y | X = x)$或$F_{Y|X}(y|x)$

相互独立的随机变量

设$F(x,y)$及$F_X(x),F_Y(y)$分别是二维随机变量$(X,Y)$的分布函数及边缘函数，若对于所有$x,y$有

$\begin{aligned} P(X \leq x, Y \leq y) &= P(X \leq x)P(Y \leq y) \\ F(x,y) &= F_X(x)F_Y(y) \end{aligned}$

连续型随机变量相互独立

设$(X,Y)$是连续型随机变量，$f(x,y)$，$f_X(x)$，$f_Y(y)$分布为$(X,Y)$的概率密度和边缘概率密度，则$X$和$Y$相互独立的条件为

$f(x,y) = f_X(x)f_Y(y)$

离散型随机变量相互独立

设$(X,Y)$是离散型随机变量，$P(X=x_i,Y=y_j)$，$P(X = x_i)$，$P(Y = y_i)$分布为$(X,Y)$的联合分布律和边缘分布律，则$X$和$Y$相互独立的条件为

$P(X=x_i, Y=y_j) = P(X=x_i)P(Y=y_i)$

总结

	离散型随机变量	连续型随机变量
概率	$P(X = x_k) = p_k, \quad k =1,2,\cdots$	$f(x)$
(分布/概率密度)函数	$F(x) = P(X \leq x), \quad \infty < x < \infty$	$F(x) = \int^x_{-\infty}f(t)dt$

	离散型二维随机变量	连续型二维随机变量
联合(分布/概率)函数	$F(x,y) = P((X \leq x) \cup (Y \leq y)) =P(X \leq x, Y \leq y)$	$F(x,y) = \int^y_{-\infty}\int^x_{-\infty}f(u,v)du,dv$
边缘分布函数	$\begin{aligned}p_{i \cdot} = \sum^\infty_{j=1}p_{ij} = P(X = x_i), \quad i=1,2,\cdots\\p_{\cdot j} = \sum^\infty_{i=1}p_{ij} = P(Y = y_i), \quad j=1,2,\cdots\end{aligned}$	$\begin{aligned}f_X(x) = \int^\infty_{-\infty}f(x,y)dy\\f_Y(y) = \int^\infty_{-\infty}f(x,y)dx\end{aligned}$
条件分布	$\begin{aligned}P(X = x_i\vert Y = y_i) = \frac{P(X = x_i, Y = y_i)}{P(Y = y_j)} = \frac{p_{ij}}{p_{\cdot j}}, \quad i=1,2,\cdots\\P(Y = y_i\vert X = x_i) = \frac{P(X = x_i, Y = y_i)}{P(X = x_i)} = \frac{p_{ij}}{p_{i\cdot}}, \quad j=1,2,\cdots\end{aligned}$	$\begin{aligned}\int^x_{-\infty} f_{X\vert Y}(x\vert y)dx = \int^x_{-\infty}\frac{f(x,y)}{f_Y(y)}dx\\\int^y_{-\infty} f_{Y\vert X}(y\vert x)dy = \int^y_{-\infty}\frac{f(y,x)}{f_X(x)}dy\end{aligned}$
相互独立	$\begin{aligned}P(X=x_i, Y=y_j) = P(X=x_i)P(Y=y_i)\end{aligned}$	$f(x,y) = f_X(x)f_Y(y)$

公式

把$n$个物品，分配到$x, y, z$三组的分法：

$p = \frac{n!}{x!\cdot y!\cdot z!}$

• $1 - P(A) = P(\overline{A})$
• $1 - P(A|B) = P(\overline{A}|B)$
• $P(A) = P(AB \cup A\overline{B}) = P(AB) + P(A\overline{B})$
• $P(A \cup B) = P(A) + P(B) - P(AB)$