[线性代数] - 矩阵论

什么是线性空间

定义：设$F$是一个非空数集，且$0,1\in F$，若对$F$中任意元素$a,b$，有

$\begin{aligned} a + b &\in F \\ a - b &\in F \\ a \cdot b &\in F \\ a / b &\in F (b \neq 0) \end{aligned}$

则称F为数域

定义：设$F$是一个数域，$V$是一非空集合，对$V$中的任意元素$a,b$，定义加法运算$+$，且有

$a + b \in V$

对$F$中任意元素$k$，以及$V$中任意元素$a$，定义数乘运算$\cdot$，且有

$k \cdot a \in V$

若加法与数乘满足一下性质，则称$V$为数域$F$上的线性空间，记为$V(F)$

• 加法

  • 交换率：$a + b = b + a$
  • 结合率：$(a+b)+c=a+(b+c)$
  • 零元： $\exists O \in V, \forall a \in V \rightarrow O + a = a$
  • 负元： $\forall a \in V, \exists b \in V \rightarrow a + b = O$

• 数乘

  • 结合率：$\forall k, l \in F, a \in V \rightarrow (kl)a = k(la)$
  • 单位元：$\forall a \rightarrow 1a = a$
  • 分配律：$\forall k, l \in F, a \in V \rightarrow (k+l)a = ka + la$
  • 分配律：$\forall k \in F, a, b \in V \rightarrow k(a+b) = ka + kb$

线性空间里的元素称为向量
实线性空间：数域$F$是实数域
复线性空间：数域$F$是复数域

线性空间本质

实际就是个给元素装配了加法和数乘的非空集合
你要想玩代数游戏，就必须要有游戏规则和场地范围。

线性空间的性质

• 线性空间$V(F)$中的零元是唯一的
• 线性空间$V(F)$中的负元是唯一的
• $\forall a \in V(F) \rightarrow 0 \cdot a = O, (-1) \cdot a = -a$
• $\forall a \in V(F) \rightarrow k \cdot O = O$

线性相关

设$\lbrace a_1, a_2, \cdots, a_n \rbrace$是线性空间$V$中的一组向量，若存在一组不全为$0$的的数：

$\lbrace x_1, x_2, \cdots, x_n \rbrace$

使得

$x_1a_1 + x_2a_2 + \cdots + x_na_n = 0$

则称向量组$\lbrace a_1, a_2, \cdots, a_n\rbrace$线性相关

线性无关

设$\lbrace a_1, a_2, \cdots, a_n\rbrace$是线性空间$V$中的一组向量，若存在一组不全为$0$的的数：

$\lbrace x_1, x_2, \cdots, x_n \rbrace$

均有

$x_1a_1 + x_2a_2 + \cdots + x_na_n \neq 0$

则称向量组$\lbrace a_1, a_2, \cdots, a_n\rbrace$线性无关

基与维数

设$\lbrace a_1, a_2, \cdots, a_n\rbrace$是线性空间$V$中的一组线性无关向量组，若对$V$中任意向量$b$，存在一组数：

$\lbrace x_1, x_2, \cdots, x_n \rbrace$

使得$b = x_1a_1 + x_2a_2 + \cdots + x_na_n$
则称向量组$\lbrace a_1, a_2, \cdots, a_n\rbrace$为$V$的基，称$V$为$n$维线性空间，记为$V^n$，维数记为$\dim{V}=n$

简单来说就是线性空间$V$中的任意向量都能由这一组线性无关向量组线性表示出来，由此可见

一个线性空间可以有多组基。不同的基与基之间可以通过过渡矩阵进行变换。

向量的坐标

设$\lbrace a_1,a_2,\cdots,a_n\rbrace$是线性空间$V^n$中的基，则对$V^n$中任意向量$b$，有唯一的线性表示：

$b = x_1a_1 + x_2a_2 + \cdots + x_na_n$

记$\mathbf{x} = [x_1, x_2, \cdots, x_n]^T$
称$x$为向量$b$在基$\lbrace a_1, a_2, \cdots, a_n \rbrace$下的坐标

记$B = \lbrace a_1, a_2, \cdots, a_n \rbrace$
则有

$b = x_1a_1 + x_2a_2 + \cdots + x_na_n = Bx$

过渡矩阵

设$B_a=\lbrace a_1, a_2, \cdots, a_n\rbrace, B_b=\lbrace b_1,b_2,\cdots,b_n\rbrace$是$V^n$的两个基，对基$B_b$中任意向量$b_i$，可以求出在基$B_a$下的坐标。设为

$P_i = \begin{bmatrix} p_{i1} & p_{i2} & \cdots & p_{in} \end{bmatrix}$

写成向量形式：

$b_i = B_aP_i \quad (i = 1, 2, \cdots, n)$

记$P=[P_1, P_2, \cdots, P_n]$，由此得到

$B_b = B_a \cdot P$

过度矩阵性质

• 过度矩阵是满秩矩阵
• 若$P$是基$B_a$到基$B_b$的过渡矩阵，则$P^{-1}$是基$B_b$到基$B_a$的过渡矩阵
• 若向量$a$在基$B_a$下的坐标是$x$，即$a=B_ax$，则向量$a$在$B_b$下的坐标是$y=P^{-1}x$

子空间

设$V$是数域$F$上的线性空间，是$W$的$V$子集，若对$W$中的任意元素$a,b$，及数$k\in F$，按$V$中的加法和数乘有：

$\begin{aligned} a+b &\in W \\ ka &\in W \end{aligned}$

则$W$也是数域$F$上的线性空间，称$W$为$V$的线性子空间

常见子空间

• 零空间：$N(A) = \lbrace x \in R | Ax = 0\rbrace$
  • $\dim{N(A)} = n -rankA = n -r$
• 列空间：$R(A) = \lbrace Ax | x \in R^n\rbrace$
  • $\dim{R(A)} = rankA = r$

Span

设$\lbrace a_1, a_2, \cdots, a_n\rbrace$是线性空间$V$的一向量，记

$Span\lbrace a_1, a_2, \cdots, a_n\rbrace = \lbrace a = \sum^r_{i=l}k_ia_i | k_1, k_2, \cdots, k_r \in F\rbrace$

则$Span\lbrace a_1, a_2, \cdots, a_n\rbrace$是$V$的子空间，称为由$\lbrace a_1, a_2, \cdots, a_n\rbrace$张成的子空间

• 若$\lbrace a_1, a_2, \cdots, a_n\rbrace$是子空间$W$的基，则有

$W = span\lbrace a_1, a_2, \cdots, a_n\rbrace$

• 设$A \in \mathbb{R}^{m\times n}$，记$A = \begin{bmatrix}A_1 & A_2 & \cdots & A_n\end{bmatrix}$，其中$A_i \in \mathbb{R}^m, i = 1,2, \cdots, n$
  则有

$R(A) = \lbrace Ax | x \in \mathbb{R}^n\rbrace = Span\lbrace A_1, A_2, \cdots, A_n\rbrace$

基扩张定理

设$\lbrace a_1, a_2, \cdots, a_r\rbrace$是$V^n$中一组线性无关向量，则存在$V^n$中$n-r$个向量$\lbrace a_{r+1}, a_{r+2}, \cdots, a_n\rbrace$使得

$\lbrace a_1, a_2, \cdots, a_r, a_{r+1}, \cdots, a_n\rbrace$

构成$V^n$的基

和空间与交空间

• 和空间：$W_1 \cap W_2$
• 交空间：$W_1 + W_2$

设有$W_1 = Span\lbrace a_1, \cdots, a_r\rbrace, W_2 = Span\lbrace b_1, \cdots, b_r\rbrace$，则有

$W_1 + W_2 = Span\lbrace a_1, \cdots, a_r, b_1, \cdots, b_r\rbrace$

维数公式

设$W_1, W_2$是线性空间$V$的两个子空间，则有

$\dim{(W_1+W_2)}+\dim{(W_1 \cap W_2)}=\dim{W_1}+dim{W_2}$

直和

设$W_1$和$W_2$是线性空间$V$的子空间，若对$\forall a \in W_1+W_2, \exists a = a_1 + a_2 (a_1∈W_1, a_2∈W_2 )$且是唯一的，这个和$W_1+W_2$就称为直和，记为

$W_1 \oplus W_2$

也就是，$W_1, W_2$中的任一向量只能唯一地分解为$W_1$中的一个向量与$W_2$中的一个向量直和，则$W_1+W_2$为$W_1$和$W_2$的直和

下列条件等价

• $W_1 + W_2 = W_1 \oplus W_2$
• $W_1 \cap W_2 = \lbrace O\rbrace$
• $\dim{(W_1 + W_2)} = \dim{W_1} + \dim{W_2}$
• $O = a_1 + a_2, a_1 \in W_1, a_2 \in W_2$，则有$a_1 = O, a_2 = O$

线性变换

定义： 设$V_1, V_2$是同一数域$F$上的线性空间，$T$是$V_1 \rightarrow V_2$的映射，若对$V_1$中任意向量$a, b$，以及数域$F$中任意元素$k$，有

$\begin{aligned} T(a+b) &= Ta+Tb \\ T(ka) &= kTa \end{aligned}$

则称$T$为线性空间$V_1$到$V_2$的线性变换

线性变换的矩阵表示

设$T$是$V^n \rightarrow V^m$的线性变换，$B_a = \lbrace a_1, a_2, \cdots, a_n\rbrace$与$B_b = \lbrace b_1, b_2, \cdots, b_n\rbrace$分别是$V^n, V^m$的基，则

$V^n \stackrel{T}{\rightarrow} V^m$

因为$Ta_i \in V^m$，设$Ta_i$在基$B_b = \lbrace b_1, b_2, \cdots, b_m\rbrace$下的坐标为

$A_i = \begin{bmatrix} a_{1i} & a_{2i} & \cdots & a_{mi} \end{bmatrix}$

既有$Ta_i = B_nA_i (i = 1, 2, \cdots, n)$

记$TB_a = \lbrace Ta_1, Ta_2, \cdots, Ta_n\rbrace$
则有

$\begin{aligned} TB_a &= \lbrace Ta_1, Ta_2, \cdots, Ta_n\rbrace \\ &= \lbrace B_bA_1, B_bA_2, \cdots, B_bA_n\rbrace \\ &= B_b\lbrace A_1, A_2, \cdots, A_n\rbrace \\ &= B_bA \end{aligned}$

定义：称矩阵$A$为线性变换$T$在奇偶$\lbrace B_a,B_b\rbrace$下的矩阵，若$T$是$V^n \rightarrow V^n$(自身)的线性变换，则取$B_b = B_a$，此时$A$是方阵，简称为$T$在基$B_a$下的矩阵

$A = \begin{bmatrix} a_{1} & a_{2} & \cdots & a_{n} \end{bmatrix}$

其中$A_i$是像$Ta_i$在像空间基$B_b$下的坐标。

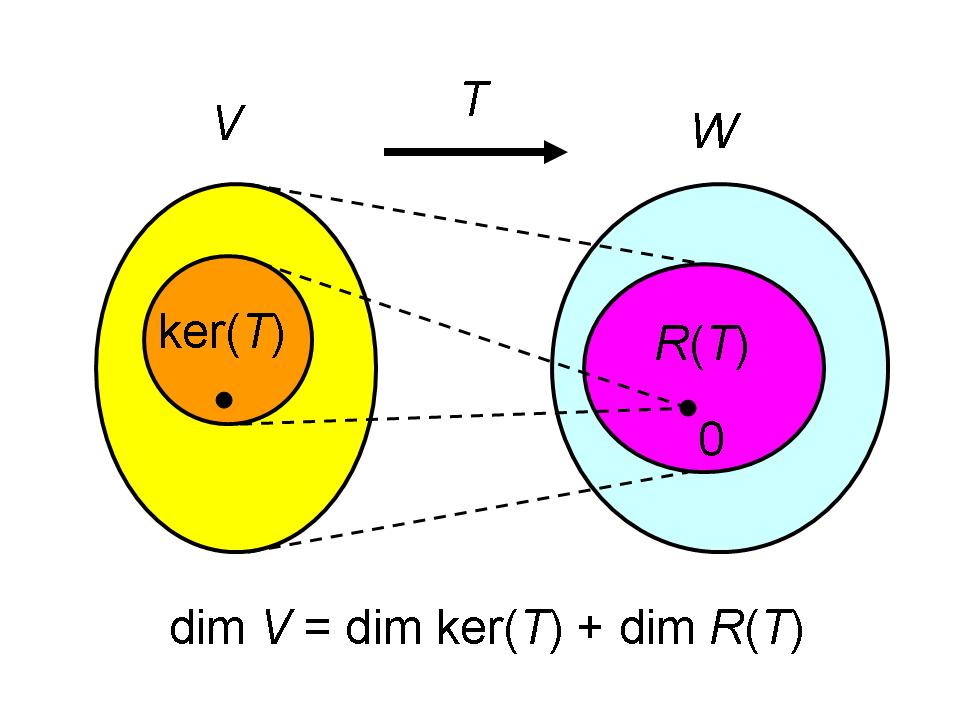
零空间与值空间

设$T$是$V^n \rightarrow V^m$的线性变换，记
T的零空间(核)：$N(T) = \lbrace x \in V^n | Tx = O\rbrace$
T的值空间(值域)：$R(T) = \lbrace Tx \in V^m | x \in V^n\rbrace$

如果把$T$看作矩阵$A$，则变为矩阵的零空间，值空间。

$null(T)=\dim{N(T)}$：为$T$的零度
$rank(T)=\dim{R(T)}$：为$T$的秩

因为$Ta_i \in V^m, i =1, 2, \cdots, n$
设$Ta_i$在基$B_b = \lbrace b_1, b_2, \cdots, b_m\rbrace$下的坐标为

$A= \begin{bmatrix} a_{1i} & a_{2i} & \cdots & a_{ni} \end{bmatrix}$

既有$Ta_i = B_bA_i, i = 1, 2, \cdots, n$
设$T$是$V^n \rightarrow V^m$的线性变换，$B_a = \lbrace a_1, a_2, \cdots, a_n\rbrace$与$B_b = \lbrace b_1, b_2, \cdots, b_n\rbrace$分别是$V^n, V^m$的基，则

• $null(T) = \dim{N(A)} = n - rank(A)$
• $rank(T) = \dim{R(A)} = rank(A)$
• $rank(T) + null(T) = n$

$T$是抽象的，难以计算，而$A$实际存在，方便计算。

线性变换在不同奇偶下的矩阵

设$T$是$V^n \rightarrow V^m$的线性变换
$B_a, B_{\tilde{a}}$是$V^n$的两个基，$B_b, B_{\tilde{b}}$是$V^m$的两个基
$T$在奇偶$\lbrace B_a, B_b\rbrace$下的矩阵为A，即$TB_a = B_bA$
$T$在奇偶$\lbrace B_{\tilde{a}}, B_{\tilde{b}}\rbrace$下的矩阵为B，即$TB_{\tilde{a}} = B_{\tilde{b}}A$

矩阵$A$与$B$有什么关系？
设$B_a$到$B_{\tilde{a}}$的过渡矩阵为P，$B_b$到$B_{\tilde{b}}$的过渡矩阵为Q。
即

$\begin{cases} B_{\tilde{a}} = B_aP \\ B_{\tilde{b}} = B_bQ \end{cases}$

我们先看

$\begin{aligned} TB_a &= B_bA \\ B_{\tilde{a}} &= B_aP \end{aligned}$

我们在两边同时乘上T

$\begin{aligned} TB_{\tilde{a}} &= T(B_aP) \\ &= T(B_a)P \\ &= (B_bA)P \\ &= B_b(AP) \end{aligned}$

再看

$\begin{aligned} TB_{\tilde{a}} &= B_{\tilde{b}}A \\ B_{\tilde{b}} &= B_bP \end{aligned}$

我们在两边同时乘上T

$\begin{aligned} TB_{\tilde{a}} &= B_{\tilde{b}}B \\ &= (B_{\tilde{b}}Q)B \\ &= B_b(QB) \end{aligned}$

由矩阵坐标的唯一性，我们可以得到

$AP = QB \Rightarrow A = QBP^{-1}$

说明：线性变换在不同奇偶下的矩阵是等价的

我们重新假设T是$V_n \rightarrow V_n$的线性变换，也就是指向自身的线性变换。我们同样可以得到

$AP = PB \Rightarrow A = PBP^{-1}$

说明：线性变换在不同奇偶下的矩阵是相似的

寻找线性变换$T$

目标：找到$V^n$上的一个基$B$，使得$T$在基$B$下的矩阵具有比较简单的形式

• 对角阵
• 分块对角阵

不变子空间

设$T$是$V^n$上的线性变换，$W$是$V^n$的子空间，若对$\forall a \in W \rightarrow Ta \in W$，称$W$是$T$的不变子空间。
设$T$是$V^n$上的线性变换，则

• $T$的零空间$N(T)$是$T$的不变子空间
• $T$的值空间$R(T)$是$T$的不变子空间

线性变换的特征值与特征向量

设$T$是$V^n$上的线性变换，若存在数$\lambda$，及非零向量$\xi$,使得

$T\xi = \lambda \xi$

则称$\lambda$为T的特征值，称$\xi$为$T$关于$\lambda$的特征向量
记$V_\lambda = \lbrace \xi \in V^n | T\xi = \lambda \xi\rbrace$
则$V_\lambda$是$V^n$的子空间，称之为$T$关于特征值$\lambda$的特征子空间，称$\dim{V_\lambda}$为$\lambda$的集合重数

设$B = \lbrace a_1, a_2, \cdots, a_n\rbrace$是$V^n$的基，$T$在基$B$下的矩阵为$A$，
设向量$\xi$在基$B$下的坐标为$x$，即$\xi = Bx$，则

$T \xi = T(Bx) = (TB)x = BAx$

所以

$T \xi = \lambda \xi \Leftrightarrow BAx = B\lambda x \Leftrightarrow Ax = \lambda x$

即$\lambda$是$T$的特征值，当且仅当$\lambda$是$A$的特征值。

线性变换的对角化

设$T$是$V^n$上的线性变换，若存在$V^n$上的一个基$B$，使得$T$在该基下的矩阵是对角阵，则称$T$可对角化
$T$可对角化的充要条件是下列等价条件之一成立

• $T$有$n$个线性无关的特征向量
• $V^n = V_{\lambda 1} \oplus V_{\lambda 2} \oplus \cdots \oplus V_{\lambda s}$，其中$\lambda_1, \lambda_2, \cdots, \lambda_s$是$T$的所有可能特征值。

内积

设$V$是实数域R上的线性空间，$\forall x, y \in V$，$V$上的内积是这样一个映射$V×V→R$，记为$<x, y>$，满足以下性质

• 对称性：$<x, y> =<y, x>$
• 可加性：$<x+y, z> =<x, z>+<y, z>$
• 齐次性：$<kx, y> =k<x, y>$
• 非负性：$<x, x> ≥ 0$，仅当$x=0$时有$<x, x>=0$

则称$<x, y>$为$a$与$b$的内积
定义了内积的实线性空间称为欧氏空间(实内积空间)

---

设$V$是复线性空间，$\forall x, y \in V$，$V$上的内积是这样一个映射$V×V→R$，记为$<x, y>$，满足以下性质

• 共轭对称性：$<x, y> = \overline{<y, x>}$
• 可加性：$<x+y, z> = <x, z>+<y, z>$
• 齐次性：$<kx, y> = k<x, y>$
• 非负性：$<x, x> ≥ 0$，仅当$x=0$时有$<x, x>=0$

则称$<x, y>$为$a$与$b$的内积
定义了内积的复线性空间称为酉空间

内积的定义

对任意的$x y \in \mathbb{R}^n$，令

$<x, y> = x^Ty = y^Tx = \sum_{i=1}^n x_iy_i$

易验证上式子定义的$<x, y$>是内积

---

设$A \in \mathbb{R}^{n\times n}$是给定的一个正定矩阵，对任意的$x, y \in \mathbb{R}^n$，令

$<x, y> = x^TAy = y^TAx = \sum^n_{i=1} \sum^n_{j=1} x_{i}a_{ij}y_{j}$

可验证上式定义的$<x, y>$是内积

内积的性质

• $<a, O> = 0$
• $<a, b + \xi> = <a, b> + <a + \xi>$
• $<a, kb> = k<a, b>$
• $<\sum^n_{i=1}x_ia_i, \sum^m_{j=1}y_jb_j> = \sum^n_{i=1}\sum^n_{j=1}x_i<a_i, b_j>y_j$

向量长度

设$V$是欧氏空间，对任意的$a \in V$，称

$|a| = \sqrt{<a, a>}$

为向量$a$的长度，称长度为$1$的向量为**单位向量
若$a \neq O$，记$a^0 = \frac{a}{|a|}$，称为向量$a$的单位化向量

向量的正交

设$V$是欧氏空间，$a, b \in V$，若

$<a, b> = 0$

则称向量$a$与$b$相互正交，记为$a \perp b$

勾股定理

设$V$是欧氏空间$a, b \in V$，若

$a \perp b$

即向量$a$与$b$正交，则有

$|a+b|^2 = |a|^2 + |b|^2$

正交向量组

设$a_1, a_2, \cdots, a_n$是欧式空间$V$中的非零向量，若$a_1, a_2, \cdots, a_n$两两正交，则称之为正交向量组

若$a_1, a_2, \cdots, a_n$两两正交，则他们线性无关

标准正交基

设$B = \lbrace a_1, a_2, \cdots, a_n\rbrace$是$n$维欧式空间$V^n$中的正交向量组，则称$B$为$V^n$的正交基

又若$B = \lbrace a_1, a_2, \cdots, a_n\rbrace$中向量均为单位向量，则称$B$为$V^n$的单位正交基

$n$维欧式空间$V^n$必存在标准正交基

正交补空间

设$W_1, W_2$都是欧式空间$V$中的子空间，若对任意的$a \in W_1, b \in W_2$，都有

$<a, b> = 0, \quad a \perp b$

则称$W_1$与$W_2$相互正交，记为$W_1 \perp W_2$

若$W_1 \perp W_2$，则$W_1 + W_2 = W_1 \oplus W_2$

正交补

设$W_1, W_2$都是欧式空间$V$中的子空间，若有

$W_1 \perp W_2, V = W_1 \oplus W_2$

则称$W_1$与$W_2$互为正交补，记为

$W_1 = W_2^\perp, W_2 = W_1^\perp$

称

$V = W_1 \oplus W_1^\perp = W_2 \oplus W_2^\perp$

为$V$的正交直和分解

欧氏空间$V^n$的任一子空间$W$都有唯一的正交补$W^\perp$

正交变换

设$T$是欧氏空间$V^n$上的线性变换，若对任意的$a, b \in V^n$，有

$<Ta, Tb> = <a, b>$

称$T$为$V^n$上的正交变换

下列条件等价：

• $T$是正交变换
• $T$是保持向量长度不变，即对任意的$a \in V^n$，有$|Ta| = |a|$
• $T$将标准正交基映射为标准正交基
• $T$在标准正交基下的矩阵为正交矩阵

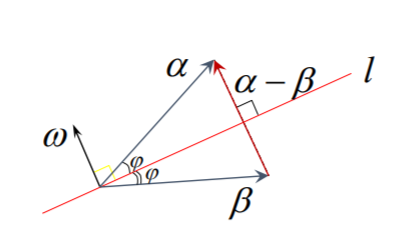
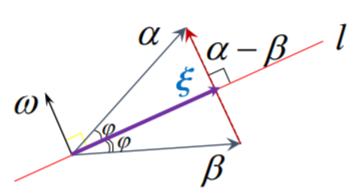
镜像变换

在平面上取定一单位向量$\omega$，以及与$\omega$正交且过原点的一条直线$l$，讲任一向量$a$映射为与直线$l$对称的向量$b$

即定义了平面上的一映射

$Ta = b$

因为在平面上，向量$a-b$与$\omega$均与直线$l$正交，所以向量$a-b$与$\omega$线性相关
设$a-b = k\omega$

• $\xi \perp \omega$
• $\xi = a - \frac{a-b}{2} = a - \frac{kw}{2}$

$\begin{aligned} 0 &= <\xi, \omega> \\ &= <a, \omega> - \frac{k<\omega, \omega>}{2} \end{aligned}$

由此的$k = 2<a, \omega>$
既有$b = Ta = a - 2<a, \omega>\omega$

$\begin{aligned} b &= Ta = a - 2 <a, \omega>\omega \\ &= a - 2w\omega<a, \omega> = a - 2\omega(\omega^Ta) \\ &= a - 2\omega\omega^Ta = (I - 2\omega\omega^T)a \end{aligned}$

记$H_\omega = I - 2\omega\omega^T$，则有

• $H_\omega^T = H_\omega$
• $H_\omega^2 = I$
• $H_\omega$是正交矩阵

镜像变换定义

在$\mathbb{R}^n$中取定一单位向量$\omega$，令

$H_\omega = I - 2\omega\omega^T$

则对任意向量$a$，定义线性变换$T$如下

$Ta = H_\omega a$

称之为镜像变换(或Householder变换)
称矩阵$H = I - 2\omega\omega^T$为Householder矩阵
易知$T$是正交变换

对称变换

设$T$是欧氏空间$V^n$上的线性变换，则$T$是对称变换的充要条件是$T$在标准正交基下的矩阵是对称矩阵

奇异矩阵

当$|A| = 0$，时，$A$称为奇异矩阵，否则称为非奇异矩阵

奇异矩阵就是Singular Matrix。看见Singular，那么就是单身了，也就是这个矩阵时没有对象的（逆矩阵）

酉矩阵

设$A$是$n$阶复方阵，若有

$A^HA=AA^H=I$

则称$A$为酉矩阵.

• 酉矩阵是正交矩阵的推广，且$A^{-1} = A^H$
• $A$是酉矩阵$\Leftrightarrow A$的列向量两两正交

正定矩阵

当且经当对于所有的非零实系数向量$z$，都有$z^TAz > 0$的矩阵$A$是正定矩阵

• 矩阵$A$的所有特征值都是正的
• 所有的主子矩阵$A_k$都具有正的行列式，$A_k = A(1 : k,1 : k)$由矩阵$A$的第$1 ∼ k$行和第$1 ∼k$列组成
• 存在一个非奇异的$n \times n$矩阵$R$使得$A = R^TR$
• 存在一个非奇异的$n \times n$矩阵$P$使得$P^TAP$是正定的。

定理

若$A$是非奇异矩阵，那么$A^TA$为正定矩阵
证明：
设$x \neq 0$，有

$x^T(A^TA)x = (Ax)^T(Ax)=\parallel Ax\parallel^2 \geq 0$

因为$A$是非奇异矩阵（$A$的列向量线性无关），所以仅当$x = 0$时才有$Ax = 0$，因此$A^TA$为正定矩阵。

正规矩阵

设$A$是$n$阶复方阵，若有

$AA^H=A^HA$

则称$A$为正规矩阵

• 设$A$为正规矩阵，$A$与$B$酉相似，则$B$为正规矩阵
  证明：

$\begin{aligned} B &= U^{-1}AU \\ &= U^HAU \\ \\ BB^H &= U^HAU(U^HAU)^H \\ &= U^HAUU^HA^HU \\ &= U^HAA^HU \\ &= U^HA^HAU \\ &= U^HA^HUU^HAU \\ &= (U^HAU)^H(U^HAU) = B^HB \end{aligned}$

Hermite矩阵

设$A$是$n$阶复方阵，若有

$A^H=A$

则称$A$为Hermite矩阵

Hermite矩阵是对称矩阵的推广

Hermite矩阵性质

$A$是正定矩阵

证明：

$A$的特征值全是实数

证明：
令$\lambda$和$\mu$分别是Hermite矩阵$A$特征值和与之对应的特征向量，即

$A\mu=\lambda\mu$

计算二项式$\mu^HA\mu$

$\begin{aligned} \mu^HA\mu &= \mu^H (A \mu) \\ &= \mu^H (\lambda \mu) \\ &= \lambda \mu^H \mu \\ \\ \mu^H A^H \mu &= (\mu^H A^H) \mu \\ &= (A\mu)^H \mu \\ &= (\lambda\mu)^H \mu \\ &= \lambda^H \mu^H \mu \end{aligned}$

两式相减

$(\lambda - \lambda^H)\mu^H\mu = 0$

因为$\mu^H\mu = \sum_{i=1}^n\parallel u_i\parallel ^2 \neq 0$，则

$\begin{aligned} \lambda - \lambda^H &= 0 \\ \lambda &= \lambda^H \end{aligned}$

说明特征值全为实数。

$A$的属于不同特征值的特征向量相互正交

设$\lambda_1, \mu_1$和$\lambda_2, \mu_2$是Hermite矩阵$A$的2对特征对。则

$\begin{aligned} Au_1 &= \lambda_1 \mu_1 \\ Au_2 &= \lambda_2 \mu_2 \end{aligned}$

相互乘对方的共轭转置

$\begin{aligned} \mu^T_2A\mu_1 &= \lambda_1 \mu^T_2 \mu_1 \\ \mu^T_1A\mu_2 &= \lambda_2 \mu^T_1 \mu_2 \end{aligned}$

对其中一个式子取共轭转置

$\mu^T_1A\mu_2 = \lambda_1 \mu^T_1 \mu_2$

可以得出

$\lambda_1 \mu^T_1 \mu_2 = \lambda_2 \mu^T_1 \mu_2$

两式相减

$(\lambda_1 - \lambda_2) \mu^T_1 \mu_2 = 0$

因为$\lambda_1 \neq \lambda_2$，则$\mu^T_1 \mu_2 = 0$，所以$\mu_1 \mu_2$相互正交。

$A^{-1}$的特征值是$\lambda^{-1}$

设$\lambda, \mu$是Hermite矩阵$A$的特征对。若$A$可逆，则$\frac{1}{\lambda}, \mu$是逆矩阵$A^{-1}$的特征对
证明：

$\begin{aligned} A\mu &= \lambda \mu \\ \mu &= \lambda A^{-1}\mu \\ \lambda^{-1}\mu &= A^{-1}\mu \end{aligned}$

Schur定理

设$A$是$n$阶复方阵，则存在一酉矩阵$U$，使得$U^{-1}AU$是上三角矩阵，即

$U^{-1}AU = U^HAU = \begin{bmatrix} \lambda_1 & * & \cdots & * \\ 0 & \lambda_2 & \cdots & * \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{bmatrix}$

其中$\lambda_1, \lambda_2, \cdots, \lambda_n$是$A$的特征值

---

若$A$是$n$阶Hermite矩阵，则存在一酉矩阵$U$，使得$U^{-1}AU$是对角阵，即

$U^{-1}AU = U^HAU = \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{bmatrix}$

其中$\lambda_1, \lambda_2, \cdots, \lambda_n$是$A$的特征值

---

若$A$是实对称矩阵，则存在一正交矩阵$Q$，使得$Q^{-1}AQ = Q^TAQ$是对角阵，即

$Q^{-1}AQ = Q^TAQ = \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{bmatrix}$

其中$\lambda_1, \lambda_2, \cdots, \lambda_n$是$A$的特征值

对称变换一定可以对角化

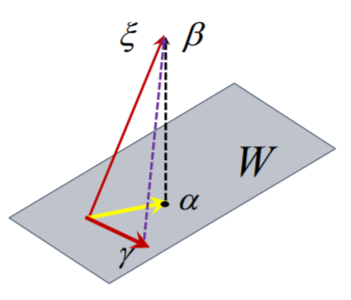
正交投影变换

设$W$是欧氏空间$V^n$的子空间，则对任意的$\xi \in V^n$，有唯一分解式

$\xi = a + b (a \in W, b \in W^\perp)$

定义$V^n$上的映射$T$

$T\xi = a$

• $T$是线性变换，称之为投影变换
• 设$\xi \in V^n$，但$\xi \notin W$，则有

$|\xi - T\xi| \leq |\xi - \gamma|, \forall \gamma \in W$

投影矩阵

假设$a_1$与$a_2$是$V$的一个基，那么必然存在$\hat{x_1}, \hat{x_2}$使得$p = \hat{x_1} + \hat{x_2}$。我们令

$\begin{aligned} A &= \begin{bmatrix} a_1 & a_2 \end{bmatrix} \\ \hat{x} &= \begin{bmatrix} \hat{x_1} \\ \hat{x_2} \end{bmatrix} \end{aligned}$

那么就有

$p = A\hat{x}$

因为$e \perp V$，因此$e$也垂直$V$的基，即$e \perp a_1, e \perp a_2$，即

$\begin{cases} \mathbf{a}_1^T \mathbf{e} = 0 \\ \mathbf{a}_2^T \mathbf{e} = 0 \end{cases} \Rightarrow \begin{bmatrix} \mathbf{a}_1^T \\ \mathbf{a}_2^T \end{bmatrix} (b - p) = 0 \Rightarrow A^T (b - A\hat{x}) = 0$

通过计算

$\begin{aligned} A^Tb - A^TA\hat{x} &= 0 \\ A^TA\hat{x} &= A^Tb \\ \hat{x} &= (A^TA)^{-1}A^Tb \end{aligned}$

两边同乘$A$

$\begin{aligned} A\hat{x} &= A(A^TA)^{-1}A^Tb \\ p &= A(A^TA)^{-1}A^Tb \end{aligned}$

令

$P = A(A^TA)^{-1}A^T$

得

$p = Pb$

这里$P$的作用是将向量$b$投影到平面$V$，因此叫做投影矩阵。

这里将$b$推广到$\mathbb{R}^m$中一个向量，$V$是$\mathbb{R}^m$下的$n(n \leq m)$维子空间，$a_1, a_2, \cdots, a_n$是$V$的一个基，那么$b$在$V$上的投影$p$可以表示为：$p = \hat{x_1}a_1 + \hat{x_2}a_2 + \cdots + \hat{x_n}a_n = A\hat{x}$，以上等式依旧成立。

矩阵的相似对角化

相似矩阵

设$A,B$是$n$方阵，若存在可逆方阵$P$，使得

$B=P^{-1}AP$

则称$A$与$B$相似，或者称$A$相似于$B$，记为$A \sim B$

矩阵相似是一种等价关系：

• 反射性：$A \sim A$
• 对称性：$A \sim B \rightarrow B \sim A$
• 传递性：$A \sim B, B \sim C \rightarrow A \sim C$

若$A$与$B$相似，则有

• $A$与$B$有相同的特征多项式与特征值
• $A$与$B$有相同的秩与行列式
• $A$与$B$有相同的迹
• 设$y = f(x)$是多项式，则$f(A)$与$F(B)$相似

相似对角化

设$A$是$n$阶方阵，若存在可逆方阵$P$，使得

$P^{-1}AP = P^HAP = \begin{bmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \end{bmatrix}$

则称矩阵$A$可相似对角化，$P$称为相似变换矩阵

• $n$阶方阵$A$可相似对角化的充要条件是$\rightarrow$$A$有$n$个线性无关的特征向量
• 若$n$阶方阵$A$有$n$个不同的特征值，则$A$可对角化

特征子空间

设$\lambda_0$是$n$阶方阵$A$的特征值，记

$E_{\lambda_0} = \lbrace x \in \mathbb{C}^n | Ax = \lambda_0x \rbrace$

$E_{\lambda_0}$：$A$关于$\lambda_0$的特征子空间
$k_0 = \dim E_{\lambda_0}$：特征值$\lambda_0$的几何重数

广义逆矩阵

一个方阵不一定可逆，长方矩阵更没有逆。那么是否推广矩阵逆的概念，让任何矩阵在某种意义下都可逆。

定义

设$A \in \mathbb{C}^{m \times n}$，若存在矩阵$G \in \mathbb{G}^{n \times m}$，使得

• $AGA = A$
• $GAG = G$
• $(AG)^H = AG$
• $(GA)^H = GA$

则称$G$为$A$的Morre-Penrose广义逆，记为$A^+$

性质

• $(A^+)^+ = A$
• $(A^*)^+ = (A^+)^*$，$(A^T)^+ = (A^+)^T$
• $(\lambda A)^+ = \lambda^+A^+$
• $diag(\lambda_1, \cdots, \lambda_n)^+ = diag(\lambda_1^+, \cdots, \lambda_n^+)$
• $A^+AA^* = A^*, A^*AA^+ = A^*, AA^+A^* = A^*, A^*A^+A = A^*$
• $(A^*A)^+ = A^+(A^+)^*$
• $A^+ = (A^*A)^+A^*$
• 若$A$是可逆，则有$A^+ = A^{-1}$
• 若$F$是列满秩，则有$F^+ = F^{-1}_L = (F^HF)^{-1}F^H$
• 若$G$是行满秩，则有$G^+ = G^{-1}_R = G^H(GG^H)^{-1}$
• 对任意矩阵$A \in \mathbb{C}^{m\times n}$，设$A$的满秩分解为$A=FG$，则有$A^+ = G^+F^+ = G^H(GG^H)^{-1}(F^HF)^{-1}F^H$
• 设$A \in \mathbb{C}^{m \times n}$，则$A$的加号逆$A^+$存在且唯一
• 设$A$的奇异值分解为$A = UDV^*$，则$A^+ = VD^+U^*$

证明：
令$G = V\Sigma^+U^H$。于是有

$\begin{aligned} AGA &= (U\Sigma V^H)(V\Sigma^+U^H)(U\Sigma V^H) \\ &= U\Sigma\Sigma^+\Sigma V^H = U\Sigma V^H = A \\ GAG &= (V\Sigma^+U^H)(U\Sigma V^H)(V\Sigma^+U^H) \\ &= V\Sigma^+\Sigma\Sigma U^H = V\Sigma U^H = G \\ AG &= (U\Sigma V^H)(V\Sigma^+U^H) \\ &= U\Sigma \Sigma^+U^H = (AG)^H \\ GA &= (V\Sigma^+U^H)(U\Sigma V^H) \\ &= V\Sigma^+\Sigma V^H = (GA)^H \end{aligned}$

$A^+$的满秩算法

• 设$A$为列满秩矩阵，则$A^+ = (A^*A)^{-1}A^*$
• 设$A$为行满秩矩阵，则$A^+ = A^*(AA^*)^{-1}$

矩阵总结

过渡矩阵：$B_b = B_aP$

对称矩阵：$A = A^T$

正交矩阵：$A^{T} = A^{-1}$

酉矩阵：$A^HA = AA^H = E$

正规矩阵：$A^HA = AA^H$

奇异矩阵：$|A| = 0$

幂等矩阵：$A = A^2$

投影矩阵：$A = A^2 = A^T$

Hermite矩阵：$A = A^H$

反Hermite矩阵：$A = -A^H$

相似矩阵：$B=P^{-1}AP$

广义逆矩阵：$AGA = A$

参考资料

• 矩阵理论学习笔记
• 【矩阵论】工程应用数学基础（国防科技大学）
• Cynhard的博客