[动态规划] - 斯坦纳树

简单来说，斯坦纳树就是将指定点的集合中的所有点连通，且边权总和最小的生成树，最小生成树其实最小斯坦纳树的一种特殊情况，也就是指定集合为全部点的情况。而斯坦纳树的点可以是所有点的任意子集。

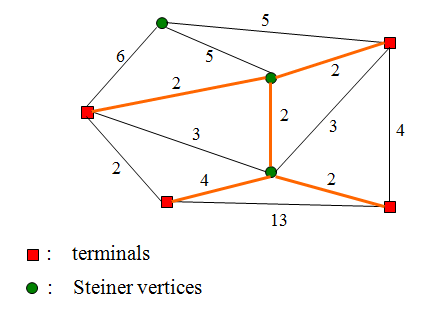
如图，红色的点即为需要连接的点，而图中红色的线所组成点树即为斯坦纳树

P、NP、NP-Complete、NP-Hard问题

为了更好的理解如何解决这个问题，我们需要理解什么是P、NP、NP-Complete、NP-Hard问题。

多项式时间复杂度：算法的复杂度表示为$O(n^k)$，也就是问题的规模$n$在底数
指数型时间复杂度：算法的复杂度表示为$O(k^n)$或$O(n!)$

P（Polynomial）问题：
可以找到一个只有多项式复杂度的算法的问题

NP（Non-Deterministic Polynomial）问题：
多项式时间内可以验证一个解的问题

通俗的说明$NP$问题，对于某些问题，我们很难找到一个多项式时间复杂度的算法，或许根本不存在算法可以解决这个问题，但是，如果给我们一个解，我们可以判断这个解是不是符合要求的，比如无法找到一个生成质数的表达式，但是我们可以验证一个数是否是质数。这就是NP问题。由此可知，所有的$P$问题都是$NP$问题。

NPH（Non-Deterministic Polynomial Hard）问题：
任意的一类$NP$问题都可以在多项式时间内归类为某个$X$问题，但是这个问题本身可能不是$NP$问题，如果我们要解决这类NP问题，我们需要解决问题$X$，而解决问题$X$就间接解决了这类$NP$问题。

NPC（Non-Deterministic Polynomial Complete）问题：
这个问题既是$NP$问题又是$NPH$问题

由于这里不是主要说明P、NP、NP-Complete、NP-Hard问题，就简洁的介绍一些。

本次要解决的斯坦纳树是$NPC$问题，我们无法找到直接生成斯坦纳树点算法，但是我们可以验证这个是不是斯坦纳树。

流程

因为我们无法直接生成斯坦纳树，我们就只能去猜结果。

• 我们先生成一个reduce tree，也就是一个接近斯坦纳树的树
• 然后我们通过增加或删除结点点方式来看修改过的reduce tree是否比上一个树更好
• 在可接受时间内，重复算法，尽可能地找到最好的结果